K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
L
1
28 tháng 10 2021
bữa sau bạn nhớ giải thích nữa nha chớ mình không biết tại sao ra đáp án đó đâu
TH
1
4 tháng 3 2022
Bài 1:
Xét ΔDEF có
M là trung điểm của DE
P là trung điểm của DF
Do đó: MP là đường trung bình
=>MP//EF
=>ΔDMP\(\sim\)ΔDEF
Xét ΔDEF có
M là trung điểm của ED
N là trung điểm của FE
Do đó: MN là đường trung bình
=>ΔEMN\(\sim\)ΔEDF
Xét ΔDEF có
P là trung điểm của DF
N là trung điểm của EF
Do đó: PN là đường trung bình
=>PN//DE
hay ΔFPN\(\sim\)ΔFDE
9 tháng 11 2021
\(a,\Leftrightarrow x^2\left(2x-3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{3}{2}\end{matrix}\right.\)
\(b,\Leftrightarrow\left(x+2\right)\left(x-1\right)+3\left(x-1\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x+2+3\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x+5\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\x=-5\end{matrix}\right.\)
\(c,\Leftrightarrow\left(3x-1\right)^2=\left(4x+6\right)^2\\ \Leftrightarrow\left[{}\begin{matrix}3x-1=4x+6\\3x-1=-4x-6\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=-7\\x=-\dfrac{5}{7}\end{matrix}\right.\)
22 tháng 10 2023
a: ABCD là hình chữ nhật
=>BC//AD
=>CI//AD
Xét tứ giác AICD có
CI//AD
CI\(\perp\)CD
Do đó: AICD là hình thang vuông
b: AK=KD=AD/2
BI=CI=BC/2
mà AD=BC
nên AK=KD=BI=CI
AD//BC
mà \(K\in AD;I\in BC\)
nên AK//CI
c: Xét tứ giác AKCI có
AK//CI
AK=CI
Do đó: AKCI là hình bình hành
=>AI//CK và AI=CK
d: ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường(1)
AICK là hình bình hành
=>AC cắt IK tại trung điểm của mỗi đường(2)
Từ (1),(2) suy ra AC,BD,IK đồng quy
9 tháng 7 2018
nhưng đây là toán 8 ,đầu năm thì đc hok hằng đẳng thức nên sẽ áp dụng theo HĐT
9 tháng 7 2018
đề e đăng sai rồi,sửa:
\(\left(2x+1\right)\left(4x^2-2x+1\right)-\left(8x^3-1\right)\)
\(=8x^3+1-8x^3+1\)
\(=2\)
Vậy gt bt trên ko phụ thuộc vào biến.
7 tháng 11 2021
Câu 5:
Vì E,F là trung điểm AD,BC nên EF là đtb tg ABC
Do đó \(EF=\dfrac{AB+CD}{2}=4\left(cm\right)\)
Câu 6:
Vì \(\widehat{B}+\widehat{C}=\widehat{B}+\widehat{EDB}=90^0\) nên tam giác BED vuông tại E
Vì \(\widehat{C}+\widehat{B}=\widehat{C}+\widehat{HDC}=90^0\) nên tg HDC vuông tại H
Vì \(\widehat{EAH}=\widehat{AED}=\widehat{AHD}=90^0\) nên AEDH là hcn
7 tháng 11 2021
Câu 5:
Xét hình thang ABCD có
E là trung điểm của AD
F là trung điểm của BC
Do đó: EF là đường trung bình của hình thang ABCD
Suy ra: FE//AB
8 tháng 11 2021
a) \(=x^2+2x-2x=x^2\)
b) \(=4-x^2+x^2=4\)
c) \(=x^2-x^3+x^3+27=x^2+27\)
d) \(=4x^2+4xy+y^2+4x^2-8x^2-4xy=y^2\)
H9
HT.Phong (9A5)
CTVHS
23 tháng 8 2023
Bài 3:
\(I=64^2-72\cdot64+36^2\)
\(I=64^2-2\cdot36\cdot64+36^2\)
\(I=\left(64-36\right)^2\)
\(I=28^2\)
\(I=784\)
\(K=47\cdot53\)
\(K=\left(50-3\right)\left(50+3\right)\)
\(K=50^2-3^2\)
\(K=2500-9\)
\(K=2491\)
\(M=123^3-69\cdot123^2+369\cdot23^2-23^3\)
\(M=123^3-3\cdot23\cdot123^2+3\cdot123\cdot23^2-23^3\)
\(M=\left(123-23\right)^3\)
\(M=100^3\)
\(M=1000000\)
\(N=54^3+138\cdot54^2+162\cdot46^2+46^3\)
\(N=54^3+3\cdot46\cdot54^2+3\cdot54\cdot46^2+46^3\)
\(N=\left(54+46\right)^3\)
\(N=100^3\)
\(N=1000000\)
KV
23 tháng 8 2023
Bài 1
A = 3(x - 1)² - (x + 1)² + 2(x - 3)(x + 3)
= 3x² - 6x + 1 - x² - 2x - 1 + 2x² - 18
= (3x² - x² + 2x²) + (-6x - 2x) + (1 - 1 - 18)
= 4x² - 8x - 18
B = 5x(x - 7)(x + 7) - 2(2x - 1)²
= 5x³ - 245x - 8x² + 8x - 2
= 5x³ - 8x² + (-245x + 8x) - 2
= 5x³ - 8x² - 237x - 2
C = (x² - 2)(x² + 2) - x² + 4
= x⁴ - 4 - x² + 4
= x⁴ - x²
D = (4x - 1)(1 + 16x + 4x) - (4x + 1)³
= 4x + 80x² - 1 - 20x - 64x³ - 48x² - 12x - 1
= -64x³ + (80x² - 48x²) + (4x - 20x - 12x) + (-1 - 1)
= -64x³ + 32x² - 28x - 2
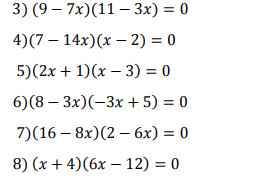
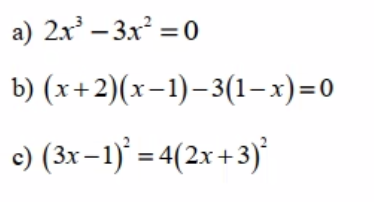
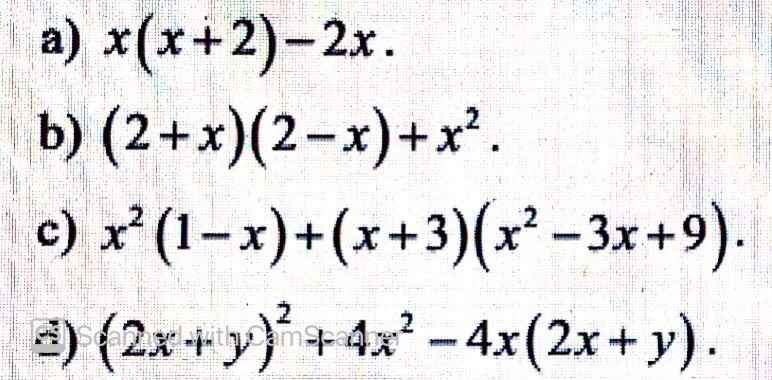
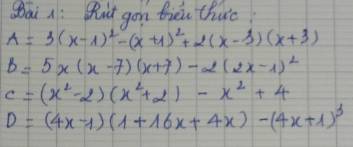
\(3,\left(9-7x\right)\left(11-3x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{9}{7}\\x=\dfrac{11}{3}\end{matrix}\right.\)
\(4,\left(7-14x\right)\left(x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=2\end{matrix}\right.\)
\(5,\left(2x+1\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=3\end{matrix}\right.\)
Câu còn lại cũng tương tự
3) \(\left\{{}\begin{matrix}9-7x=0\\11-3x=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-7x=-9\\-3x=-11\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{9}{7}\\x=\dfrac{11}{3}\end{matrix}\right.\)
4)\(\left\{{}\begin{matrix}7-14x=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-14x=-7\\x=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{7}{14}\\x=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\x=2\end{matrix}\right.\)
5)\(\left\{{}\begin{matrix}2x-1=0\\x-3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=1\\x=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\x=3\end{matrix}\right.\)
6)\(\left\{{}\begin{matrix}8-3x=0\\-3x+5=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-3x=-8\\-3x=-5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{8}{3}\\x=\dfrac{5}{3}\end{matrix}\right.\)
7)\(\left\{{}\begin{matrix}16-8x=0\\2-6x=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-8x=-16\\-6x=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\x=\dfrac{1}{3}\end{matrix}\right.\)
8)\(\left\{{}\begin{matrix}x+4=0\\6x-12=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-4\\6x=12\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-4\\x=2\end{matrix}\right.\)