K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 5 2021
b.
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x< 2\\x>\dfrac{9}{2}\end{matrix}\right.\\-\dfrac{1}{3}< x< 7\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}-\dfrac{1}{3}< x< 2\\\dfrac{9}{2}< x< 7\end{matrix}\right.\)
Hay \(S=\left(-\dfrac{1}{3};2\right);\left(\dfrac{9}{2};7\right)\)
d.
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x\le-\dfrac{11}{5}\\x\ge7\end{matrix}\right.\\-\dfrac{1}{2}< x< 3\end{matrix}\right.\) \(\Rightarrow x\in\varnothing\) hay BPT vô nghiệm
15 tháng 6 2023
b: C=sin(x-pi/2+2pi)+sin(x+pi)+cos(pi/2-x)+cos(pi/2+x)
=sin(x-pi/2)+sin(x+pi)+sinx+cos(pi/2+x)
=-sin(pi/2-x)-sinx+sinx-sinx=-cosx-sinx
15 tháng 6 2023
\(D=\dfrac{sin2x+2\cdot cos4x\cdot sinx}{cosx+cos4x}=\dfrac{2\cdot sinx\left(cosx+cos4x\right)}{cosx+cos4x}=2\cdot sinx\)
b: C=sin(x-pi/2+2pi)+sin(x+pi)+cos(pi/2-x)+cos(pi/2+x)
=sin(x-pi/2)+sin(x+pi)+sinx+cos(pi/2+x)
=-sin(pi/2-x)-sinx+sinx-sinx=-cosx-sinx
VT
1
4 tháng 12 2021
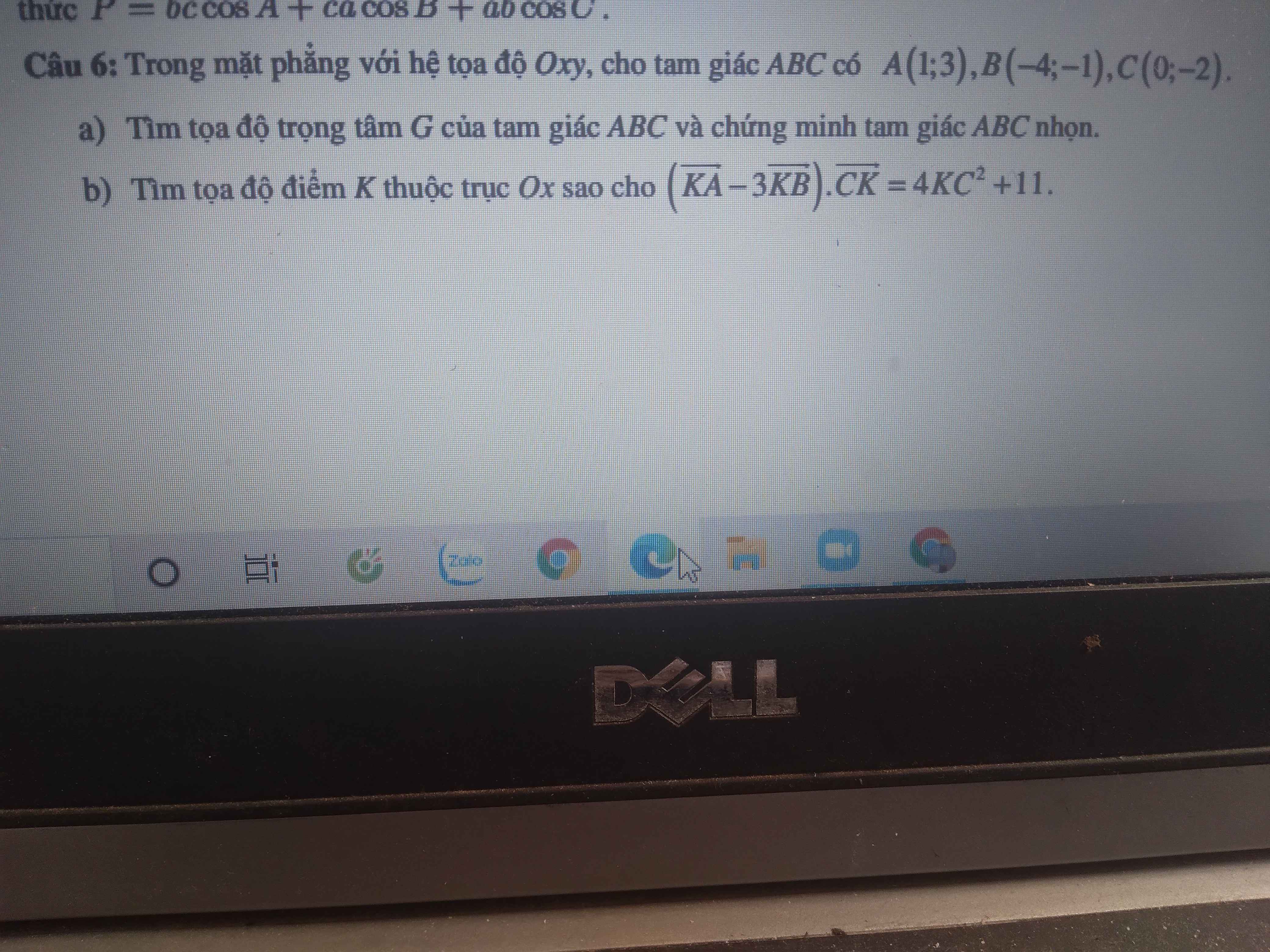
a: \(\left\{{}\begin{matrix}\overrightarrow{AB}=\left(x_B-x_A;y_B-y_A\right)=\left(-5;-4\right)\\\overrightarrow{AC}=\left(x_C-x_A;y_C-y_A\right)=\left(-1;-5\right)\end{matrix}\right.\)
Vì -5:(-1)<>(-4):(-5) nên A,B,C không thẳng hàng
hay ΔABC nhọn
3 tháng 12 2021
a: \(\left\{{}\begin{matrix}x_G=\dfrac{x_A+x_B+x_C}{2}=\dfrac{1-4+0}{2}=\dfrac{-3}{2}\\y_G=\dfrac{y_A+y_B+y_C}{2}=\dfrac{3-1-2}{2}=0\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 4 2021
a. \(sinx+cosx=\dfrac{1}{5}\Rightarrow\left(sinx+cosx\right)^2=\dfrac{1}{25}\Rightarrow sin^2x+cos^2x+2sinx.cosx=\dfrac{1}{25}\)
\(\Rightarrow1+2sinx.cosx=\dfrac{1}{25}\Rightarrow sinx.cosx=-\dfrac{12}{25}\)
\(P=tanx+cotx=\dfrac{sinx}{cosx}+\dfrac{cosx}{sinx}=\dfrac{sin^2x+cos^2x}{sinx.cosx}=\dfrac{1}{sinx.cosx}=\dfrac{1}{-\dfrac{12}{25}}=-\dfrac{25}{12}\)
b. \(\left(tana-cota\right)^2=\left(2\sqrt{3}\right)^2\Leftrightarrow\left(tana+cota\right)^2-4tana.cota=12\)
\(\Rightarrow\left(tana+cota\right)^2-4=12\Rightarrow\left(tana+cota\right)^2=16\)
\(\Rightarrow\left|tana+cota\right|=4\)
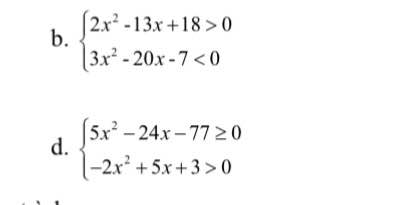
C là đáp án đúng
ĐKXĐ: \(x\ge2\)
\(\sqrt{x-2}\left(x^2-3x-2\right)=0\Leftrightarrow\left[{}\begin{matrix}\sqrt{x-2}=0\\x^2-3x-2=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=2\\x=\dfrac{3+\sqrt{17}}{2}\\x=\dfrac{3-\sqrt{17}}{2}< 2\left(loại\right)\end{matrix}\right.\)