
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


i) \(5\dfrac{8}{17}:x+\left(-\dfrac{4}{17}\right):x+3\dfrac{1}{7}:17\dfrac{1}{3}=\dfrac{4}{11}\)
\(\Rightarrow\dfrac{93}{17}:x-\dfrac{4}{17}:x+\dfrac{33}{182}=\dfrac{4}{11}\)
\(\Rightarrow\left(\dfrac{93}{17}-\dfrac{4}{17}\right):x=\dfrac{4}{11}-\dfrac{33}{182}\)
\(\Rightarrow\dfrac{89}{17}:x=\dfrac{365}{2002}\)
\(\Rightarrow x=\dfrac{89}{17}:\dfrac{365}{2002}=\dfrac{178178}{6205}\)
j) \(\dfrac{17}{2}-\left|2x-\dfrac{3}{4}\right|=-\dfrac{7}{4}\)
\(\Rightarrow\left|2x-\dfrac{3}{4}\right|=\dfrac{17}{2}-\left(-\dfrac{7}{4}\right)=\dfrac{41}{4}\)
\(\Rightarrow\left[{}\begin{matrix}2x-\dfrac{3}{4}=\dfrac{41}{4}\\2x-\dfrac{3}{4}=-\dfrac{41}{4}\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}2x=11\Rightarrow x=\dfrac{11}{2}\\2x=-\dfrac{19}{2}\Rightarrow x=-\dfrac{19}{4}\end{matrix}\right.\)
k) \(\left(x+\dfrac{1}{5}\right)^2+\dfrac{17}{25}=\dfrac{26}{25}\)
\(\Rightarrow\left(x+\dfrac{1}{5}\right)^2=\dfrac{26}{25}-\dfrac{17}{25}=\dfrac{9}{25}=\left(\dfrac{3}{5}\right)^2\)\(=\left(-\dfrac{3}{5}\right)^2\)
\(\Rightarrow\left[{}\begin{matrix}x+\dfrac{1}{5}=\dfrac{3}{5}\Rightarrow x=\dfrac{2}{5}\\x+\dfrac{1}{5}=-\dfrac{3}{5}\Rightarrow x=-\dfrac{4}{5}\end{matrix}\right.\)
l) \(-1\dfrac{5}{27}-\left(3x-\dfrac{7}{9}\right)^3=-\dfrac{24}{27}\)
\(\Rightarrow\left(3x-\dfrac{7}{9}\right)^3=\dfrac{-32}{27}-\left(-\dfrac{24}{27}\right)=-\dfrac{8}{27}=\left(-\dfrac{2}{3}\right)^3\)
\(\Rightarrow3x-\dfrac{7}{9}=-\dfrac{2}{3}\)
\(\Rightarrow3x=-\dfrac{2}{3}+\dfrac{7}{9}=\dfrac{1}{9}\)
\(\Rightarrow x=\dfrac{1}{27}\)
j, \(\dfrac{17}{2}-\left|2x-\dfrac{3}{4}\right|=\dfrac{-7}{4}\)
\(\Rightarrow-\left|2x-\dfrac{3}{4}\right|=\dfrac{-7}{4}-\dfrac{17}{2}\)
\(\Rightarrow-\left|2x-\dfrac{3}{4}\right|=\dfrac{-41}{4}\)
\(\Rightarrow\left|2x-\dfrac{3}{4}\right|=\dfrac{41}{4}\)
\(\Rightarrow\left[{}\begin{matrix}2x-\dfrac{3}{4}=\dfrac{41}{4}\\2x-\dfrac{3}{4}=\dfrac{-41}{4}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\dfrac{11}{2}\\x=\dfrac{-19}{4}\end{matrix}\right.\)
k, \(\left(x+\dfrac{1}{5}\right)^2+\dfrac{17}{25}=\dfrac{26}{25}\)
\(\Rightarrow\left(x+\dfrac{1}{5}\right)^2=\dfrac{9}{25}\)
\(\Rightarrow x+\dfrac{1}{5}=\pm\dfrac{3}{5}\)
\(\Rightarrow\left[{}\begin{matrix}x+\dfrac{1}{5}=\dfrac{3}{5}\\x+\dfrac{1}{5}=\dfrac{-3}{5}\end{matrix}\right.\Rightarrow}\left[{}\begin{matrix}x=\dfrac{2}{5}\\x=\dfrac{-4}{5}\end{matrix}\right.\)
l, \(-1\dfrac{5}{27}-\left(3x-\dfrac{7}{9}\right)^3=\dfrac{-24}{27}\)
\(\Rightarrow-\left(3x-\dfrac{7}{9}\right)^3=\dfrac{-19}{27}\)
\(\Rightarrow\left(3x-\dfrac{7}{9}\right)^3=\dfrac{19}{27}\)
\(\Rightarrow3x-\dfrac{7}{9}=\dfrac{\sqrt[3]{19}}{3}\)
\(\Rightarrow3x=\dfrac{\sqrt[3]{19}}{3}+\dfrac{7}{19}\)
\(\Rightarrow...\)

\(\dfrac{200-\left(3+\dfrac{2}{3}+\dfrac{2}{4}+\dfrac{2}{5}+...+\dfrac{2}{100}\right)}{\dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}+...+\dfrac{99}{100}}\\ =\dfrac{200-\left(2+1+\dfrac{2}{3}+\dfrac{2}{4}+\dfrac{2}{5}+...+\dfrac{2}{100}\right)}{\left(1-\dfrac{1}{2}\right)+\left(1-\dfrac{1}{3}\right)+\left(1-\dfrac{1}{4}\right)+...+\left(1-\dfrac{99}{100}\right)}\\ =\dfrac{200-2-1-\dfrac{2}{3}-\dfrac{2}{4}-\dfrac{2}{5}-...-\dfrac{2}{100}}{\left(1+1+1+...+1\right)-\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{100}\right)}\\ =\dfrac{198-\left(\dfrac{2}{2}+\dfrac{2}{3}+\dfrac{2}{4}+\dfrac{2}{5}+...+\dfrac{2}{100}\right)}{99-\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{100}\right)}\\ =\dfrac{2\cdot99-2\cdot\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{100}\right)}{99-\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{100}\right)}\\ =\dfrac{2\cdot\left[99-\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{100}\right)\right]}{99-\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{100}\right)}\\ =2\)
Đề nhỏ quá!! mà t 4 mắt. cẩn thận
Đặt :
\(A=\dfrac{200-\left(3+\dfrac{2}{3}+\dfrac{2}{4}+\dfrac{2}{5}+.............+\dfrac{2}{100}\right)}{\dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}+....................+\dfrac{99}{100}}\)
\(A=\dfrac{200-2-\left(\dfrac{2}{2}+\dfrac{2}{3}+\dfrac{2}{4}+..............+\dfrac{2}{100}\right)}{1-\dfrac{1}{2}+1-\dfrac{1}{3}+.................+1-\dfrac{1}{100}}\)
\(A=\dfrac{198-\left(\dfrac{2}{2}+\dfrac{2}{3}+..................+\dfrac{2}{100}\right)}{\left(1+1+.....+1\right)-\left(\dfrac{1}{2}+\dfrac{1}{3}+...........+\dfrac{1}{100}\right)}\)
\(A=\dfrac{2\left[99-\left(\dfrac{1}{2}+\dfrac{1}{3}+.............+\dfrac{1}{100}\right)\right]}{99-\left(\dfrac{1}{2}+\dfrac{1}{3}+..............+\dfrac{1}{100}\right)}\)
\(A=2\)
Vậy \(\dfrac{200-\left(3+\dfrac{2}{3}+\dfrac{2}{4}+............+\dfrac{2}{100}\right)}{\dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}+...............+\dfrac{99}{100}}=2\rightarrowđpcm\)

Số học sinh nam là:
\(36\cdot\dfrac{4}{9}=16\) (học sinh)
Số học sinh nữ là:
\(36-16=20\) (học sinh)
Vậy lớp 6a1 có 16 học sinh nam, 20 học sinh nữ.
Số học sinh nam của lớp là
36 .4/9 = 16 ( học sinh )
Số học sinh nữ là : 36 - 16 =20 ( h/s)


gọi \(x\) là độ dài cạnh hình vuông
\(\Rightarrow\) diện tích hình vuông ban đầu là \(x^2\)
đội dài cạnh hình vuông lúc sau là \(x+2\)
\(\Rightarrow\) diện tích hình vuông lúc sau là \(\left(x+2\right)^2\)
vì sau khi thay đổi thì diện tích hình vuông đó tăng thêm \(32m^2\) nên ta có phương trình
\(x^2+32=\left(x+2\right)^2\Leftrightarrow x^2+32=x^2+4x+4\)
\(\Leftrightarrow\) \(4x+4-32=0\Leftrightarrow4x-28=0\Leftrightarrow4x=28\)
\(\Leftrightarrow\) \(x=\dfrac{28}{4}=7\)
vậy diện tích lúc đầu của hình vuông là \(x^2=7^2=49\)\(m^2\)
Bài tui sai tiếp ak!
Tuấn Anh Phan Nguyễn a xóa giúp e zới! Nhất định hậu tạ!

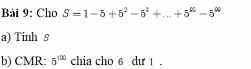

 giúp tớ với
giúp tớ với
\(a,S=1-5+5^2-5^3+...+5^{98}-5^{99}\\ 5S=5-5^2+5^3-5^4+...+5^{99}-5^{100}\\ 5S+S=1-5^{100}\\ S=\dfrac{1-5^{100}}{6}\)
\(Do\) \(S\in Z\Rightarrow1-5^{100}⋮6\Rightarrow5^{100}\) chia 6 dư 1