
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, - 1 ≤ cosx ≤ 1 ⇔ - 1 ≤ - cosx ≤ 1
⇔ 4 ≤ 5 - cosx ≤ 6
⇔ 4 ≤ y ≤ 6.
Vậy ymin = 4 khi cosx = 1 ⇔ x = k2π
ymax = 6 khi cosx = - 1 ⇔ x = π + k2π
b, - 1 ≤ sinx ≤ 1 ⇔ - 4 ≤ 4sinx ≤ 4
⇔ - 3 ≤ 4sinx + 1 ≤ 5 ⇔ - 3 ≤ y ≤ 5
ymin = - 3 khi sinx = - 1
ymax = 5 khi sinx = 1
c, sinx - cosx + 7
= \(\sqrt{2}sin\left(x-\dfrac{\pi}{4}\right)\) + 7
min = 7 - \(\sqrt{2}\) và max = 7 + \(\sqrt{2}\)
d, Đặt cosx = t ta có hàm số f(t) = 3t2 + t - 2 với t ϵ [- 1 ; 1]
Dùng BBT của hs bậc 2 là được
e, chuyển sin2x = 1 - cos2x
f, \(\sqrt{3}sinx-cosx=2sin\left(x-\dfrac{\pi}{6}\right)\)
g, \(sinx+\sqrt{3}cosx=2sin\left(x+\dfrac{\pi}{3}\right)\)
h, Đặt a = arcsin\(\dfrac{4}{5}\) = arcsin\(\dfrac{3}{5}\)
⇒ 3sinx + 4cosx = 5 sin (x + a) với a = arcsin\(\dfrac{4}{5}\) = arcsin\(\dfrac{3}{5}\)
i, 2sin2x - 1 = - cos2x
k, 7 - 2sin2x . cosx = 7 - (1- cos2x) . cosx
= 7 + cos2x . cosx - cosx
= 7 + \(\dfrac{1}{2}cos3x+\dfrac{1}{2}cosx-cosx\)
= 7 + \(\dfrac{1}{2}cos3x-\dfrac{1}{2}cosx\)
Ta có - 1 ≤ cos3x ≤ 1; -1 ≤ - cosx ≤ 1
nên cos3x - cosx ∈ [- 2 ; 2]
Từ đó suy ra min max. Dấu bằng có xảy ra

Đường tròn (C) tâm \(I\left(1;-1\right)\) bán kính \(R=4\)
Gọi \(I'\left(x';y'\right)\) là tâm \(\left(C'\right)\) \(\Rightarrow I'\) là ảnh của I qua phép vị tự nói trên đồng thời \(R'=\left|k\right|R\)
\(\left\{{}\begin{matrix}x'=1+k\left(1-1\right)=1\\y'=-1+k\left(-1+1\right)=-1\end{matrix}\right.\)
Phương trình (C'):
\(\left(x-1\right)^2+\left(y+1\right)^2=16k^2\)
Thế tọa độ M vào ta được:
\(\left(4-1\right)^2+\left(3+1\right)^2=16k^2\Rightarrow k^2=\dfrac{25}{16}\)
\(\Rightarrow k=\pm\dfrac{5}{4}\)



Đăng ảnh trực tiếp thì không được, nhưng bạn đăng ngay dưới bình luận như vầy thì thoải mái (trong khung bình luận có chỗ tải ảnh lên cạnh biểu tượng emo mặt cười đó)
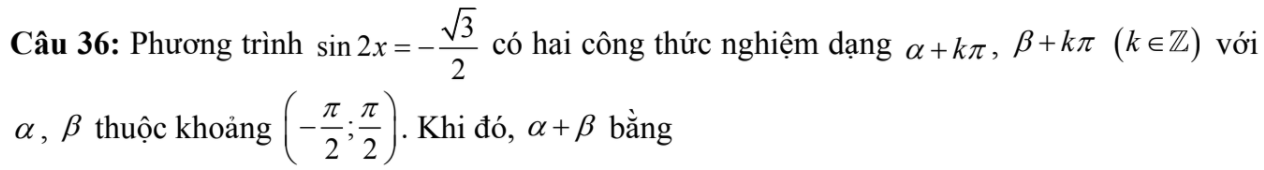 giúp mk với ạ
giúp mk với ạ



