
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 2:
1) \(x^2-4=x^2-2^2=\left(x-2\right)\left(x+2\right)\)
2) \(1-4x^2=1^2-\left(2x\right)^2=\left(1-2x\right)\left(1+2x\right)\)
3) \(4x^2-9=\left(2x\right)^2-3^2=\left(2x+3\right)\left(2x-3\right)\)
4) \(9-25x^2=3^2-\left(5x\right)^2=\left(3-5x\right)\left(3+5x\right)\)
5) \(4x^2-25=\left(2x\right)^2-5^2=\left(2x+5\right)\left(2x-5\right)\)
6) \(9x^2-36=\left(3x\right)^2-6^2=\left(3x-6\right)\left(3x+6\right)\)
7) \(\left(3x\right)^2-y^2=\left(3x-y\right)\left(3x+y\right)\)
8) \(x^2-\left(2y\right)^2=\left(x-2y\right)\left(x+2y\right)\)
9) \(\left(2x\right)^2-y^2=\left(2x-y\right)\left(2x+y\right)\)
10) \(\left(3x\right)^2-9y^4=\left(3x\right)^2-\left(3y^2\right)^2=\left(3x-3y^2\right)\left(3x+3y^2\right)\)
Bài 2:
21) \(\left(\dfrac{x}{3}-\dfrac{y}{4}\right)\left(\dfrac{x}{3}+\dfrac{y}{4}\right)=\left(\dfrac{x}{3}\right)^2-\left(\dfrac{y}{4}\right)^2=\dfrac{x^2}{9}-\dfrac{y^2}{16}\)
22) \(\left(\dfrac{x}{y}-\dfrac{2}{3}\right)\left(\dfrac{x}{y}+\dfrac{2}{3}\right)=\left(\dfrac{x}{y}\right)^2-\left(\dfrac{2}{3}\right)^2=\dfrac{x^2}{y^2}-\dfrac{4}{9}\)
23) \(\left(\dfrac{x}{2}+\dfrac{y}{3}\right)\left(\dfrac{x}{2}-\dfrac{y}{3}\right)=\left(\dfrac{x}{2}\right)^2-\left(\dfrac{y}{3}\right)^2=\dfrac{x^2}{4}-\dfrac{y^2}{9}\)
24) \(\left(2x-\dfrac{2}{3}\right)\left(\dfrac{2}{3}+2x\right)=\left(2x-\dfrac{2}{3}\right)\left(2x+\dfrac{2}{3}\right)=\left(2x\right)^2-\left(\dfrac{2}{3}\right)^2=4x^2-\dfrac{4}{9}\)
25) \(\left(2x+\dfrac{3}{5}\right)\left(\dfrac{3}{5}-2x\right)=\left(\dfrac{3}{5}+2x\right)\left(\dfrac{3}{5}-2x\right)=\left(\dfrac{3}{5}\right)^2-\left(2x\right)^2=\dfrac{9}{25}-4x^2\)
26) \(\left(\dfrac{1}{2}x-\dfrac{4}{3}\right)\left(\dfrac{4}{3}+\dfrac{1}{2}x\right)=\left(\dfrac{1}{2}x-\dfrac{4}{3}\right)\left(\dfrac{1}{2}x+\dfrac{4}{3}\right)=\left(\dfrac{1}{2}x\right)^2-\left(\dfrac{4}{3}\right)^2=\dfrac{1}{4}x^2-\dfrac{16}{9}\)
27) \(\left(\dfrac{2}{3}x^2-\dfrac{y}{2}\right)\left(\dfrac{2}{3}x^2+\dfrac{y}{2}\right)=\left(\dfrac{2}{3}x^2\right)^2-\left(\dfrac{y}{2}\right)^2=\dfrac{4}{9}x^4-\dfrac{y^2}{4}\)
28) \(\left(3x-y^2\right)\left(3x+y^2\right)=\left(3x\right)^2-\left(y^2\right)^2=9x^2-y^4\)
29) \(\left(x^2-2y\right)\left(x^2+2y\right)=\left(x^2\right)^2-\left(2y\right)^2=x^4-4y^2\)
30) \(\left(x^2-y^2\right)\left(x^2+y^2\right)=\left(x^2\right)^2-\left(y^2\right)^2=x^4-y^4\)



Bài 1:
b) \(B=A.\dfrac{-10}{x-4}=\dfrac{x-4}{x+5}.\dfrac{-10}{x-4}=\dfrac{-10}{x+5}\)
Để B nguyên <=> x+5 nguyên mà \(x\in Z\Rightarrow x+5\inƯ\left(-10\right)=\left\{\pm1;\pm2;\pm5;\pm10\right\}\)
\(\Leftrightarrow x\in\left\{-6;-4;-3;-7;0;-10;-15;5\right\}\) kết hợp với điều kiện của x
\(\Rightarrow x\in\left\{-15;-10;-6;-7;-3;0;5\right\}\)
Bài 5:
Có \(\left|x-2018\right|+\left|2x-2019\right|+\left|3x-2020\right|\ge0\) \(\forall\)x
\(\Rightarrow x-2021\ge0\) \(\Leftrightarrow x\ge2021\)
\(\Rightarrow x-2018>0,2x-2019>0,3x-2020>0\)
PT \(\Leftrightarrow x-2018+2x-2019+3x-2020=x-2021\)
\(\Leftrightarrow5x=4036\) \(\Leftrightarrow x=\dfrac{4036}{5}< 2021\) (L)
Vậy pt vô nghiệm


Để A đạt GTLN
=>x2 -2x đạt giá trị dương nhỏ nhất
=>x2-2x=1
=>x2-2x-1=0
=>x=$1-\sqrt{2};\sqrt{2}+1$1−√2;√2+1
Vậy A ko xảy ra GTLN
Để A đạt GTLN
=>x2 -2x đạt giá trị dương nhỏ nhất
=>x2-2x=1
=>x2-2x-1=0
=>x=\(1-\sqrt{2};\sqrt{2}+1\)
Vậy A ko xảy ra GTLN

`|x-2|=2x-3(x>=3/2)`
`<=>` \(\left[ \begin{array}{l}x-2=2x-3\\x-2=3-2x\end{array} \right.\)
`<=>` \(\left[ \begin{array}{l}x=1(l)\\3x=5\end{array} \right.\)
`<=>x=5/3(Tm(`
`2)A=-x^2+2x+9`
`=-(x^2-2x)+9`
`=-(x^2-2x+1)+1+9`
`=-(x-1)^2+10<=10`
Dấu "=" xảy ra khi `x=1.`
1,
* \(|x-2|=x-2< =>x\ge2\)
\(=>x-2=2x-3< =>x=1\left(ktm\right)\)
*\(\left|x-2\right|=2-x< =>x< 2\)
\(=>2-x=2x-3< =>x=\dfrac{5}{3}\left(tm\right)\)
vậy x=5/3
2, \(A=-x^2+2x+9=-\left(x^2-2x-9\right)=-\left(x^2-2x+1-10\right)\)
\(=-\left[\left(x-1\right)^2-10\right]=-\left(x-1\right)^2+10\le10\)
dấu"=" xảy ra<=>x=1
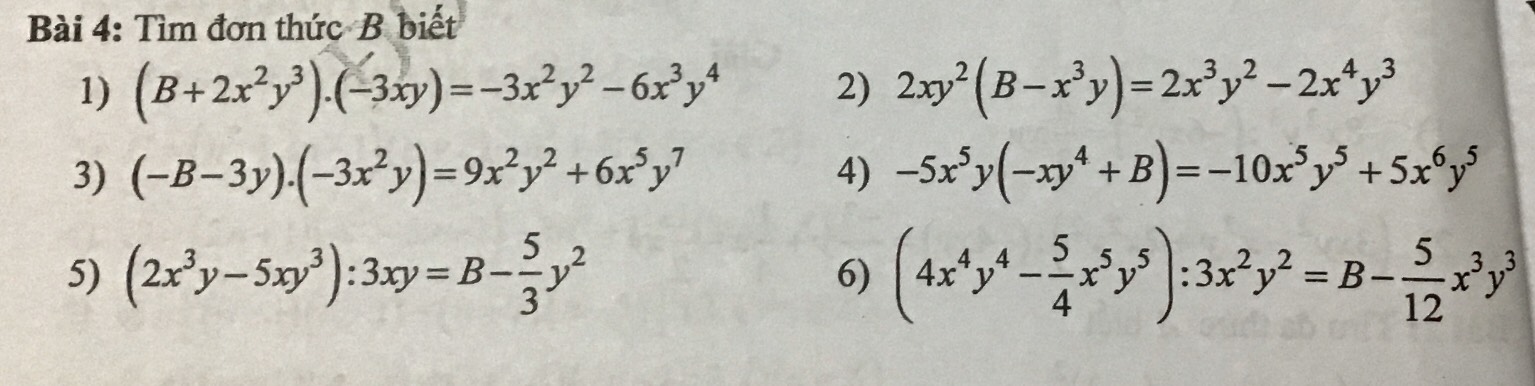

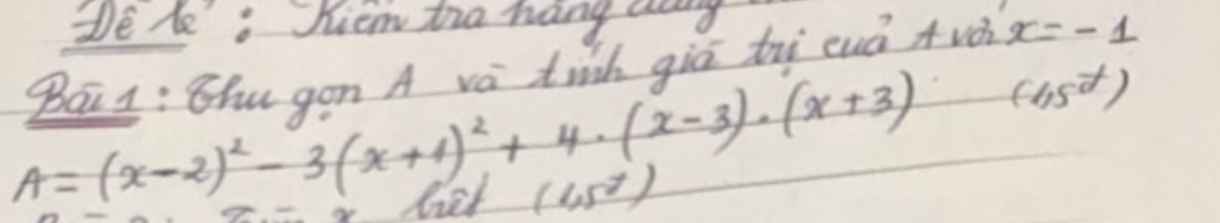


Tách ra đi bn
1: \(\Leftrightarrow B+2x^2y^3=xy+x^2y^3\)
=>B=xy-x^2y^3
2: \(\Leftrightarrow B-x^3y=x^2-x^3y\)
=>B=x^2
3: =>-B-3y=-3y-2x^3y^6
=>-B=-2x^3y^6
=>B=2x^3y^6
4: =>\(B-xy^4=2y^4-xy^4\)
=>B=2y^4
5: =>\(B-\dfrac{5}{3}y^2=\dfrac{2}{3}x^2-\dfrac{5}{3}y^2\)
=>B=2/3x^2
6: =>\(B-\dfrac{5}{12}x^3y^3=\dfrac{4}{3}x^2y^2-\dfrac{5}{12}x^3y^3\)
=>B=4/3x^2y^2