
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


2:
a: BC=căn 15^2+20^2=25cm
AH=15*20/25=12cm
góc ADH=góc AEH=góc DAE=90 độ
=>ADHE là hình chữ nhật
=>DE=AH=12cm
b: ΔAHB vuông tại H có HD vuông góc AB
nên AD*AB=AH^2
ΔAHC vuông tại H có HE vuông góc AC
nên AE*AC=AH^2
=>AD*AB=AE*AC
c: góc IAC+góc AED
=góc ICA+góc AHD
=góc ACB+góc ABC=90 độ
=>AI vuông góc ED
4:
a: góc BDH=góc BEH=góc DBE=90 độ
=>BDHE là hình chữ nhật
b: BDHE là hình chữ nhật
=>góc BED=góc BHD=góc A
Xét ΔBED và ΔBAC có
góc BED=góc A
góc EBD chung
=>ΔBED đồng dạng với ΔBAC
=>BE/BA=BD/BC
=>BE*BC=BA*BD
c: góc MBC+góc BED
=góc C+góc BHD
=góc C+góc A=90 độ
=>BM vuông góc ED


Vì \(AB//CD\) nên \(\left\{{}\begin{matrix}\widehat{B}+\widehat{C}=180^0\\\widehat{A}+\widehat{D}=180^0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}\widehat{B}=\left(180^0+40^0\right):2=110^0\\3\widehat{D}=180^0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{C}=180^0-110^0=70^0\\\widehat{D}=60^0\end{matrix}\right.\Rightarrow\widehat{A}=120^0\)
\(\widehat{B}=110^0\)
\(\widehat{C}=70^0\)
\(\widehat{A}=120^0\)
\(\widehat{D}=60^0\)

a: Ta có: AH\(\perp\)BD
CK\(\perp\)BD
Do đó: AH//CK
b: Xét ΔADH vuông tại H và ΔCBK vuông tại K có
AD=CB
\(\widehat{ADH}=\widehat{CBK}\)
Do đó: ΔADH=ΔCBK
Suy ra: AH=CK
Xét tứ giác AHCK có
AH//CK
AH=CK
Do đó: AHCK là hình bình hành
Suy ra: AK//CH

30: Ta có: \(5x-5y+ax-ay\)
\(=5\left(x-y\right)+a\left(x-y\right)\)
\(=\left(x-y\right)\left(a+5\right)\)
31: Ta có: \(6x^2-11x+3\)
\(=6x^2-9x-2x+3\)
\(=\left(2x-3\right)\left(3x-1\right)\)

\(2x^2+2y^2-4xy+2x-2y+4\)
\(=2\left(x-y\right)^2+2\left(x-y\right)+4\)
\(=2\left[\left(x-y\right)^2+2\left(x-y\right)\frac{1}{2}+\frac{1}{4}\right]+\frac{7}{2}\)
\(=2\left(x-y+\frac{1}{2}\right)^2+\frac{7}{2}\)
\(\Rightarrow A\ge\frac{7}{2}\)
Dấu = bn tự tính nhé


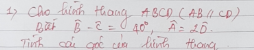

 Giúp mk lm bài này vs ạ
Giúp mk lm bài này vs ạ

`a,`
`(x+y+z)^2=[(x+y)+z]^2 =(x+y)^2 +2 (x+y)z +z^2 = x^2 +y^2 +z^2 +2xy+ 2yz +2zx` (Bằng VP)
`->` Đpcm
`b,`
`(x-y-z)^2=[(x-y)-z]^2=(x-y)^2 - 2 (x-y)z +z^2 = x^2 + y^2 +z^2 -2xy - 2zx -2yz` (Bằng VP)
`->` Đpcm