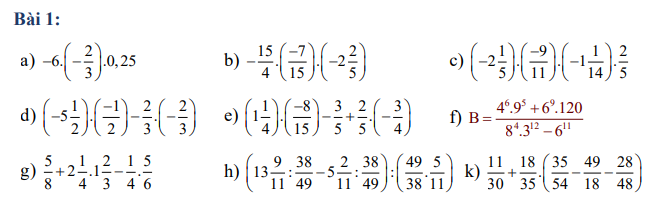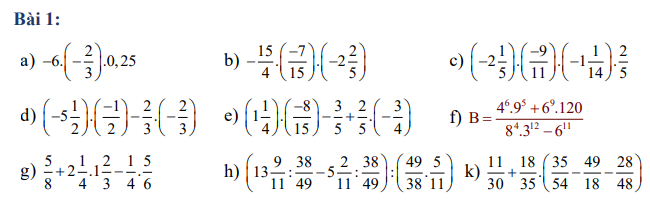Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: ΔABC cân tại A
mà AH là đường trung tuyến
nên AH vừa là đường cao, vừa là đường phân giác
Xét \(\Delta ABC\) có: AB=AC \(\Rightarrow\)\(\Delta ABC\) cân tại A
\(\Rightarrow\)AH vừa là đường trung tuyến vừa là đường cao vừa là đường phân giác của \(\widehat{A}\) trong \(\Delta ABC\)
\(\Rightarrow AH\perp BC\)

a: \(-6\cdot\left(-\dfrac{2}{3}\right)\cdot0.25=6\cdot\dfrac{2}{3}\cdot\dfrac{1}{4}=4\cdot\dfrac{1}{4}=1\)
b: \(\dfrac{-15}{4}\cdot\dfrac{-7}{15}\cdot\left(-2\dfrac{2}{5}\right)\)
\(=\dfrac{7}{4}\cdot\dfrac{12}{5}\)
\(=\dfrac{84}{20}=\dfrac{21}{5}\)
c: \(\left(-2\dfrac{1}{5}\right)\cdot\left(-\dfrac{9}{11}\right)\cdot\left(-\dfrac{1}{14}\right)\cdot\dfrac{2}{5}\)
\(=-\dfrac{11}{5}\cdot\dfrac{2}{5}\cdot\dfrac{9}{11}\cdot\dfrac{1}{14}\)
\(=-\dfrac{11}{11}\cdot\dfrac{2}{14}\cdot\dfrac{9}{25}\)
\(=-\dfrac{9}{175}\)
\(a,=4\cdot0,25=1\\ b,=\dfrac{7}{4}\cdot\left(-\dfrac{12}{5}\right)=-\dfrac{21}{5}\\ c,=\left(-\dfrac{11}{5}\right)\left(-\dfrac{9}{11}\right)\left(-\dfrac{15}{14}\right)\cdot\dfrac{2}{5}\\ =\dfrac{9}{5}\cdot\left(-\dfrac{15}{14}\right)\cdot\dfrac{2}{5}=-\dfrac{27}{14}\cdot\dfrac{2}{5}=-\dfrac{27}{35}\\ d,=\left(-\dfrac{11}{2}\right)\left(-\dfrac{1}{2}\right)+\dfrac{4}{9}=\dfrac{11}{4}+\dfrac{4}{9}=\dfrac{115}{36}\\ e,=\dfrac{5}{4}\cdot\left(-\dfrac{8}{15}\right)-\dfrac{3}{5}-\dfrac{3}{10}=-\dfrac{2}{3}-\dfrac{3}{5}-\dfrac{3}{10}=-\dfrac{47}{30}\)
\(f,B=\dfrac{2^{12}\cdot3^{10}+2^9\cdot3^9\cdot2^3\cdot3\cdot5}{2^{12}\cdot3^{12}-2^{11}\cdot3^{11}}=\dfrac{2^{12}\cdot3^{10}\left(1+5\right)}{2^{11}\cdot3^{11}\left(6-1\right)}=\dfrac{2\cdot6}{5\cdot3}=\dfrac{4}{5}\\ g,=\dfrac{5}{8}+\dfrac{9}{4}\cdot\dfrac{5}{3}-\dfrac{5}{24}=\dfrac{5}{8}+\dfrac{15}{4}-\dfrac{5}{24}=\dfrac{25}{6}\\ h,=\dfrac{49}{38}\cdot\left(\dfrac{152}{11}-\dfrac{57}{11}\right):\dfrac{245}{418}=\dfrac{49}{38}\cdot\dfrac{418}{245}\cdot\dfrac{95}{11}=\dfrac{95\cdot11}{5\cdot11}=19\\ k,=\dfrac{11}{30}+\dfrac{18}{35}\cdot\dfrac{35}{54}-\dfrac{18}{35}\cdot\dfrac{49}{18}-\dfrac{18}{35}\cdot\dfrac{28}{48}\\ =\dfrac{11}{30}+\dfrac{1}{3}-\dfrac{7}{5}-\dfrac{3}{10}=-1\)

https://hoc24.vn/cau-hoi/giai-het-giup-mk-vs-a-huhu.2030470567354
làm hết r mà :vv

Câu 6:
a: Xét ΔABM và ΔACM có
AB=AC
\(\widehat{BAM}=\widehat{CAM}\)
AM chung
Do đó: ΔABM=ΔACM

a)Ta xét trong tam giác ABH có Hˆ=90o
=>BAHˆ+ABHˆ=90o
mà BAHˆ+HACˆ=90o=Aˆ(g t)
=>ABHˆ=HACˆ.
Xét tam giác BHA và Tam giác AIC có:
AB=AC(gt)
Hˆ=AICˆ=90o(gt)
ABHˆ=HACˆ(c/m trên)
=>Tam giác BHA=Tam giác AIC(cạnh huyền-góc nhọn)
=>BH=AI(hai cạnh tương ứng)
b)Vì Tam giác BHA=Tam giác AIC(c/m trên)
=>IC=AH(hai cạnh tương ứng)
Xét trong tam giác vuông ABH có:
BH2+AH2=AB2
mà IC=AH
=>BH2+IC2=AB2(th này là D nằm giữa B và M)
Ta có thể c/m tiếp rằng D nằm giữa M và C thì ta vẫn c/m được Tam giác BHA=Tam giác AIC(cạnh huyền-góc nhọn) và BH2+IC2=AC2=AB2
=>BH2+CI2 có giá trị ko đổi
c)Ta xét trong tam giác DAC có IC,AM là 2 đường cao và cắt nhau tại N(AM cũng là đường cao do là trung tuyến của tam giác cân xuất phát từ đỉnh và cũng chính là đường cao của đỉnh đó xuống cạnh đáy=>AM vuông góc với DC)
=>DN chính là đường cao còn lại=>DN vuông góc với AC(là cạnh đối diện đỉnh đó)
d)Ta dễ dàng tính được Tam giác DMN cân tại M=>DM=MN(dựa vào số đo của các góc và 1 số c/m trên)
Từ M kẻ đường thẳng ME vuông góc với AD còn MF vuông góc với IC,Ta dễ dàng c/m được tam giác MED=Tam giác MFN(cạnh huyền-góc nhọn)
=>ME=MF(là hai đường vuông góc tại điểm M gióng xuống hai cạnh của góc HICˆ)
Theo tính chất của đường phân giác(Điểm nằm trên đường phân giác của góc này thì cách đều hai cạnh tạo thành góc đó)=>IM là tia phân giác của HICˆ.

\(\left(2x-3\right)\left(x-\dfrac{1}{2}\right)=0\\ \Rightarrow\left[{}\begin{matrix}2x-3=0\\x-\dfrac{1}{2}=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}2x=3\\x=\dfrac{1}{2}\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=\dfrac{1}{2}\end{matrix}\right.\) (Thêm KL cuối dòng: Vậy \(x\in\left\{\dfrac{3}{2};\dfrac{1}{2}\right\}\))

Lời giải:
Gọi số SGK lớp 7A, 7B, 7C quyên góp lần lượt là $a,b,c$. Theo bài ra ta có:
$\frac{a}{7}=\frac{b}{5}=\frac{c}{8}$ và $c-a=24$
Áp dụng TCDTSBN thì:
$\frac{a}{7}=\frac{b}{5}=\frac{c}{8}=\frac{c-a}{8-7}=24$
$\Rightarrow a=168; b=120; c=192$
$\Rightarrow a+b+c=480$ (quyển SGK)