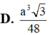Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đề bài thiếu dữ liệu định vị điểm S (ví dụ SC bằng bao nhiêu đó) nên ko thể tính góc giữa SB và (ABCD)

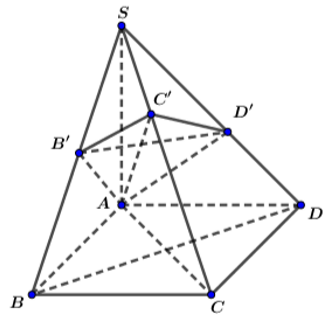
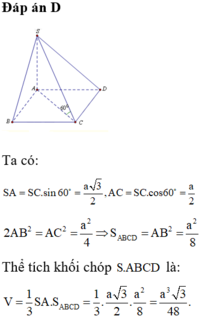
\(\begin{array}{l}\left. \begin{array}{l} + )AC \bot BD\,\,\left( {hv\,\,ABCD} \right)\\SA \bot BD\,\,\left( {SA \bot \left( {ABCD} \right)} \right)\\AC \cap SA = \left\{ A \right\}\end{array} \right\} \Rightarrow BD \bot \left( {SAC} \right)\\\left. \begin{array}{l} + )BD \bot SC\left( {BD \bot \left( {SAC} \right)} \right)\\BM \bot SC\\BD \cap BM = \left\{ B \right\}\end{array} \right\} \Rightarrow SC \bot \left( {MBD} \right)\end{array}\)
Gọi \(AC \cap BD = \left\{ O \right\}\)
\(\left. \begin{array}{l}SC \bot \left( {MBD} \right)\\OM \subset \left( {MBD} \right)\end{array} \right\} \Rightarrow SC \bot OM\)
Mà \(AH \bot SC\)
\( \Rightarrow AH//OM,OM \subset \left( {MBD} \right) \Rightarrow AH//\left( {MBD} \right)\)

+)CD⊥SA do SA vuông với ABCD
CD⊥AD( tính chất hình vuông)
=>CD⊥(SAD)=>CD⊥AN mà SD⊥AN=> AN⊥(SDC)=>AN⊥SC(1)
+) BC⊥SA do SA vuông với ABCD
BC⊥AB( tính chất hình vuông)
=>BC⊥(SAB)=>BC⊥AM mà SB⊥AM=> AM⊥(SAB)=>AM⊥SC(2)
TỪ 1 và 2 => SC⊥(AMN) đpcm

Đề đúng là SC vuông góc (ABCD) phải không nhỉ?
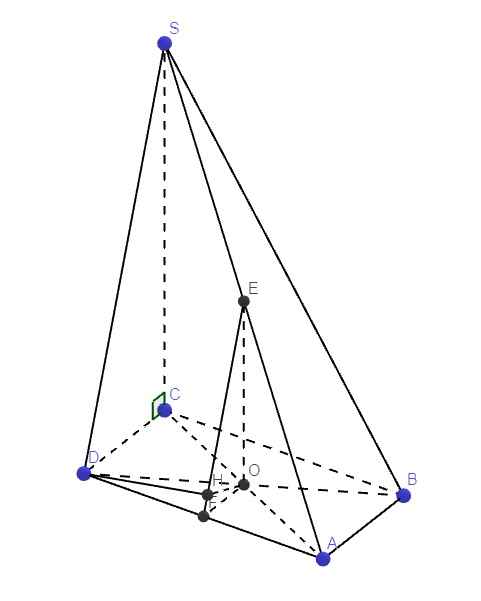
Gọi O là giao điểm AC và BD \(\Rightarrow\) O đồng thời là trung điểm AC và BD
Gọi E và F lần lượt là trung điểm SA và AD, từ O kẻ \(OH\perp EF\) (1)
OE là đường trung bình tam giác SAC \(\Rightarrow\left\{{}\begin{matrix}OE=\dfrac{1}{2}SC=\dfrac{3a}{2}\\OE||SC\Rightarrow OE\perp\left(ABCD\right)\end{matrix}\right.\)
\(\Rightarrow OE\perp AD\)
OF là đường trung bình tam giác ACD \(\Rightarrow\left\{{}\begin{matrix}OF||CD\Rightarrow OF\perp AD\\OF=\dfrac{1}{2}CD=\dfrac{a}{2}\end{matrix}\right.\)
\(\Rightarrow AD\perp\left(OEF\right)\) \(\Rightarrow AD\perp OH\) (2)
(1);(2) \(\Rightarrow OH\perp\left(SAD\right)\)
\(\Rightarrow HD\) là hình chiếu vuông góc của OD lên (SAD)
\(\Rightarrow\widehat{HDO}\) là góc giữa BD và (SAD)
Hệ thức lượng: \(\dfrac{1}{OH^2}=\dfrac{1}{OE^2}+\dfrac{1}{OF^2}\Rightarrow OH=\dfrac{OE.OF}{\sqrt{OE^2+OF^2}}=\dfrac{3a\sqrt{10}}{20}\)
\(OD=\dfrac{1}{2}BD=\sqrt{AB^2+AD^2}=\dfrac{a\sqrt{5}}{2}\)
\(\Rightarrow sin\widehat{HDO}=\dfrac{OH}{OD}=\dfrac{3\sqrt{2}}{10}\Rightarrow\widehat{HDO}\approx25^06'\)