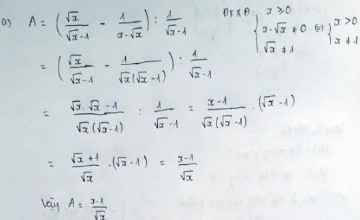Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}-x^2+x+2=0\\y=-x-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x^2-x-2=0\\y=-x-2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x-2\right)\left(x+1\right)=0\\y=-x-2\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in\left\{\left(2;-4\right);\left(-1;-1\right)\right\}\)

1)Tco ABCD là hình chữ nhật ( ADC=DCB=ABC=\(90^o\))
=> DC= AB=1,5(m)
=>AD=BC=4(m)
Xét tam giác ACE vuông tại A có đường cao AD
=>\(AD^2=DC.DE\)
\(\Leftrightarrow DE=\dfrac{AD^2}{DC}=\dfrac{16}{1,5}=10,7\)(m)
\(\Leftrightarrow CE=DE+DC=1,5+10,7=12,2\left(m\right)\)

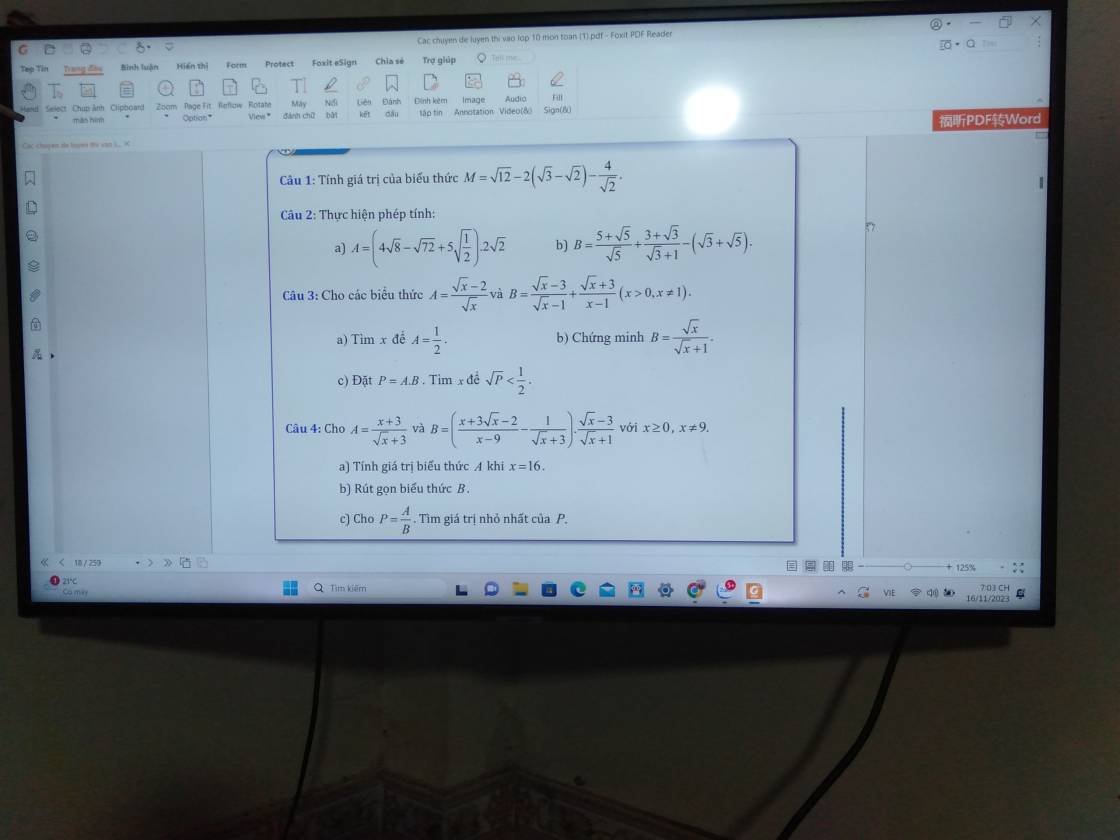
Câu 3:
a: A=1/2
=>\(\dfrac{\sqrt{x}-2}{\sqrt{x}}=\dfrac{1}{2}\)
=>\(2\sqrt{x}-4=\sqrt{x}\)
=>\(2\sqrt{x}-\sqrt{x}=4\)
=>\(\sqrt{x}=4\)
=>x=16(nhận)
b: \(B=\dfrac{\sqrt{x}-3}{\sqrt{x}-1}+\dfrac{\sqrt{x}+3}{x-1}\)
\(=\dfrac{\sqrt{x}-3}{\sqrt{x}-1}+\dfrac{\sqrt{x}+3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}+1\right)+\sqrt{x}+3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x-2\sqrt{x}-3+\sqrt{x}+3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{x-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{\sqrt{x}}{\sqrt{x}+1}\)
c: \(P=A\cdot B=\dfrac{\sqrt{x}-2}{\sqrt{x}}\cdot\dfrac{\sqrt{x}}{\sqrt{x}+1}=\dfrac{\sqrt{x}-2}{\sqrt{x}+1}\)
\(\sqrt{P}< \dfrac{1}{2}\)
=>\(0< =P< \dfrac{1}{4}\)
=>P>=0 và P<1/4
=>P>=0 và P-1/4<0
=>\(\left\{{}\begin{matrix}\dfrac{\sqrt{x}-2}{\sqrt{x}+1}>=0\\\dfrac{\sqrt{x}-2}{\sqrt{x}+1}-\dfrac{1}{4}< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\sqrt{x}-2>=0\\\dfrac{4\sqrt{x}-8-\sqrt{x}-1}{4\left(\sqrt{x}+1\right)}< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\sqrt{x}>=2\\3\sqrt{x}-9< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\sqrt{x}>=2\\\sqrt{x}< 3\end{matrix}\right.\)
=>\(2< =\sqrt{x}< 3\)
=>4<=x<9

Bạn tự tìm điều kiện xác định nhé :)
\(Q=\left(1-\frac{x-3\sqrt{x}}{x-9}\right):\left(\frac{\sqrt{x}-3}{2-\sqrt{x}}+\frac{\sqrt{x}-2}{3+\sqrt{x}}-\frac{9-x}{x+\sqrt{x}-6}\right)\)
\(=\frac{3\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}:\left(\frac{\left(3-\sqrt{x}\right)\left(\sqrt{x}+3\right)+\left(\sqrt{x}-2\right)^2-9+x}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}\right)\)
\(=\frac{3}{\sqrt{x}+3}:\frac{9-x+x-4\sqrt{x}+4-9+x}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}=\frac{3}{\sqrt{x}+3}:\frac{\left(\sqrt{x}-2\right)^2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}\)
\(=\frac{3}{\sqrt{x}+3}.\frac{\sqrt{x}+3}{\sqrt{x}-2}=\frac{3}{\sqrt{x}-2}\)

a: ĐKXĐ x>0; x<>1
\(A=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\dfrac{\sqrt{x}-1}{1}=\dfrac{x-1}{\sqrt{x}}\)
b: A<0
=>x-1<0
=>0<x<1

Gọi số người mua là x(người), doanh thu là y(đồng)
(Điều kiện: \(x\in Z^+;y>0\))
Vì doanh thu bằng số người mua nhân với lại giá của bộ quần áo nên y=320000x(đồng)
=>\(320000=\dfrac{y}{x}\)
Số người mua tăng lên 60% và doanh thu cũng tăng thêm 30% nên giá mới sẽ là:
\(\dfrac{y\cdot\left(1+30\%\right)}{x\left(1+60\%\right)}=\dfrac{y}{x}\cdot\dfrac{13}{16}=320000\cdot\dfrac{13}{16}=260000\left(đồng\right)\)

a: Khi x=25 thì \(A=\dfrac{5-2}{5-3}=\dfrac{3}{2}\)
b: P=A*B
\(=\dfrac{\sqrt{x}-2}{\sqrt{x}-3}\left(\dfrac{6x+6\sqrt{x}-12}{x+5\sqrt{x}+4}-\dfrac{5\sqrt{x}}{\sqrt{x}+4}\right)\)
\(=\dfrac{\sqrt{x}-2}{\sqrt{x}-3}\cdot\left(\dfrac{6x+6\sqrt{x}-12}{\left(\sqrt{x}+1\right)\left(\sqrt{x}+4\right)}-\dfrac{5\sqrt{x}}{\sqrt{x}+4}\right)\)
\(=\dfrac{\sqrt{x}-2}{\sqrt{x}-3}\cdot\dfrac{6x+6\sqrt{x}-12-5x-5\sqrt{x}}{\left(\sqrt{x}+4\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{x+\sqrt{x}-12}{\left(\sqrt{x}+4\right)\left(\sqrt{x}-3\right)}\cdot\dfrac{\sqrt{x}-2}{\sqrt{x}-1}=\dfrac{\sqrt{x}-2}{\sqrt{x}-1}\)
c: \(\sqrt{P}< =\dfrac{1}{2}\)
=>0<=P<=1/4
=>\(\left\{{}\begin{matrix}P>=0\\P-\dfrac{1}{4}< =0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{\sqrt{x}-2}{\sqrt{x}-1}>=0\\\dfrac{\sqrt{x}-2}{\sqrt{x}-1}-\dfrac{1}{4}< =0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left[{}\begin{matrix}x>=4\\0< =x< 1\end{matrix}\right.\\\dfrac{4\left(\sqrt{x}-2\right)-\sqrt{x}+1}{4\left(\sqrt{x}-1\right)}< =0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left[{}\begin{matrix}x>=4\\0< =x< 1\end{matrix}\right.\\\dfrac{3\sqrt{x}-7}{\sqrt{x}-1}< =0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x>=4\\0< =x< 1\end{matrix}\right.\\1< \sqrt{x}< =\dfrac{7}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x>=4\\0< =x< 1\end{matrix}\right.\\1< x< \dfrac{49}{9}\end{matrix}\right.\) hoặc \(\left\{{}\begin{matrix}\left[{}\begin{matrix}x>=4\\0< =x< 1\end{matrix}\right.\\x=\dfrac{49}{9}\end{matrix}\right.\)
=>\(4< =x< =\dfrac{49}{9}\)
mà x nguyên
nên \(x\in\left\{4;5\right\}\)

Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{2}{1}=-2\\x_1x_2=\dfrac{-1}{1}=-1\end{matrix}\right.\)
\(\Rightarrow T=x_1+x_2+3x_1x_2=-2+3.\left(-1\right)=-5\)
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-2\\x_1x_2=-1\end{matrix}\right.\)
Ta có: \(T=x_1+x_2+3x_1x_2\)
\(=-2+3\cdot\left(-1\right)\)
=-5
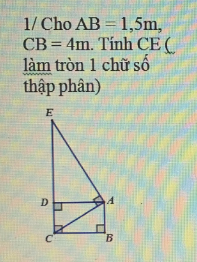 giải giúp mình vớii
giải giúp mình vớii