
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Ta có: \(P\left(x\right)=8-2x^4+x^5-3x^6+x^3-x+3x^6+2x-2\)
\(=x^5-2x^4+x^3+x+6\)
Ta có: \(Q\left(x\right)=3x^5-4x^3+2x^2-3+2x-x^5\)
\(=2x^5-4x^3+2x^2+2x-3\)
Ta có: \(P\left(x\right)+Q\left(x\right)\)
\(=x^5-2x^4+x^3+x+6+2x^5-4x^3+2x^2+2x-3\)
\(=3x^5-2x^4-3x^3+2x^2+3x+3\)
Ta có: P(x)-Q(x)
\(=x^5-2x^4+x^3+x+6-2x^5+4x^3-2x^2-2x+3\)
\(=-x^5-2x^4+5x^3-2x^2-x+9\)

\(72.\)
Xét tam giác AHC vuông tại H ta có:
\(\sin C=\dfrac{AH}{AC}\) (Tỉ số lượng giác).
\(\Rightarrow\sin30^o=\dfrac{AH}{40}.\Rightarrow AH=20.\)
Xét tam giác AHB vuông tại H:
\(AB^2=AH^2+BH^2\left(Pytago\right).\)
\(\Rightarrow29^2=20^2+BH^2.\\ \Leftrightarrow BH^2=29^2-20^2.\\ \Rightarrow BH=21.\)

Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
Suy ra: HB=HC
=>AH là đường trung tuyến
=>AH là đường trung trực
=>AH là phân giác

a) \(f\left(x\right)+g\left(x\right)-h\left(x\right)\)
\(=\left(2x^5-4^4x^4+3x^3-x^2+5x-1\right)+\left(-x^5+2x^4-3x^3-x^2-2x+7\right)-\left(x^5-2x^4-2x^2-x-3\right)\)
\(=2x^5-4x^4+3x^3-x^2+5x-1-x^5+2x^4-3x^3-x^2-2x+7-x^5+2x^4+2x^2+x+3\)\(=\left(2x^5-x^5-x^5\right)-\left(4x^4-2x^4-2x^4\right)+\left(3x^3-3x^3\right)-\left(x^2+x^2-2x^2\right)+\left(5x-2x+x\right)-\left(1-7-3\right)\)
\(=0-0+0-0+4x-9\)
\(=4x-9\)
`a,`
`f(x)+g(x)-h(x)=(2x^5-4x^4+3x^3-x^2+5x-1)+(-x^5+2x^4-3x^3-x^2-2x+7)-(x^5-2x^4-2x^2-x-3)`
`= 2x^5-4x^4+3x^3-x^2+5x-1+ -x^5+2x^4-3x^3-x^2-2x+7-x^5+2x^4+2x^2+x+3`
`= (2x^5-x^5-x^5)-(4x^4-2x^4-2x^4)+(3x^3-3x^3)-(x^2-2x^2)-(2x-x)+(-1+7+3)`
`= 0-0+0-(-x^2)-x+10 = x^2-x+9`

a: Xét ΔAMB và ΔAMC có
AB=AC
AM chung
MB=MC
Do đó: ΔAMB=ΔAMC
b: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là tia phân giác
c: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
d: Xét ΔAKB và ΔAKC có
AK chung
\(\widehat{BAK}=\widehat{CAK}\)
AB=AC
Do đó: ΔAKB=ΔAKC
Suy ra: KB=KC

7:
A+B
\(=x^4-2xy+y^2+y^2+2xy+x^2+1\)
=x^4+2y^2+x^2+1
A-B
=x^4-2xy+y^2-y^2-2xy-x^2-1
=x^4-4xy-x^2-1
5:
a: =8x^2-4x^2=4x^2
b: =(5-7)*x^2y^3z^3=-2x^2y^3z^3
c: =(3+2-1/3-1/2-1/6)*x^2y^2
=4x^2y^2

\(\widehat{IBC}+\widehat{ICB}=180^0-140^0=40^0\)
\(\Leftrightarrow\widehat{ABC}+\widehat{ACB}=2\cdot40^0=80^0\)
\(\Leftrightarrow\widehat{BAC}=100^0\)

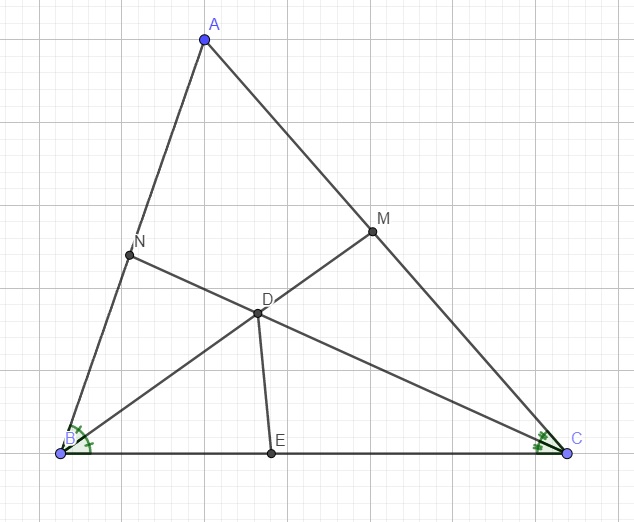
Gọi D là giao điểm BM và CN.
Trên cạnh BC lấy điểm E sao cho \(BE=BN\)
Khi đó \(CE=BC-BE=BN+CM-BE=CM\)
Xét hai tam giác BDE và BDN có:
\(\left\{{}\begin{matrix}BE=BN\\\widehat{DBE}=\widehat{DBN}\left(\text{BM là phân giác}\right)\\BD\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta BDE=\Delta BDN\left(c.g.c\right)\)
\(\Rightarrow\widehat{BDE}=\widehat{BDN}\)
Hoàn toàn tương tự, ta cũng có \(\Delta CDE=\Delta CDM\left(c.g.c\right)\Rightarrow\widehat{CDE}=\widehat{CDM}\)
Mà \(\widehat{BDN}=\widehat{CDM}\) (đối đỉnh) \(\Rightarrow\widehat{BDN}=\widehat{BDE}=\widehat{CDM}=\widehat{CDE}\)
Mà \(\widehat{BDE}+\widehat{CDE}+\widehat{CDM}=180^0\)
\(\Rightarrow3\widehat{BDE}=180^0\Rightarrow\widehat{BDE}=60^0\)
\(\Rightarrow\widehat{CDE}=60^0\)
\(\Rightarrow\widehat{BDC}=\widehat{BDE}+\widehat{CDE}=120^0\)
Theo tính chất tổng 3 góc tổng tam giác:
\(\widehat{BDC}+\widehat{DBC}+\widehat{DCB}=180^0\)
\(\Rightarrow120^0+\dfrac{1}{2}\widehat{B}+\dfrac{1}{2}\widehat{C}=180^0\)
\(\Rightarrow\widehat{B}+\widehat{C}=120^0\)
Do tổng 3 góc trong tam giác ABC bằng 180 độ
\(\Rightarrow\widehat{A}+\widehat{B}+\widehat{C}=180^0\)
\(\Rightarrow\widehat{A}+120^0=180^0\)
\(\Rightarrow A=60^0\)

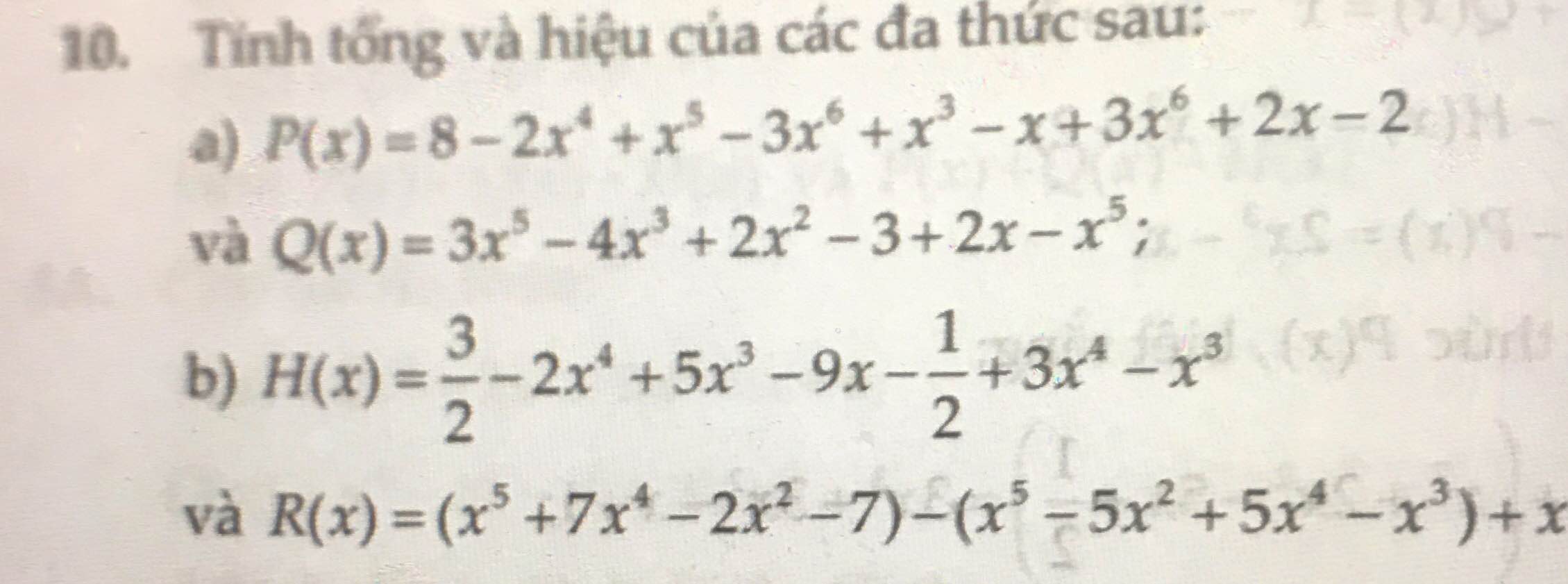
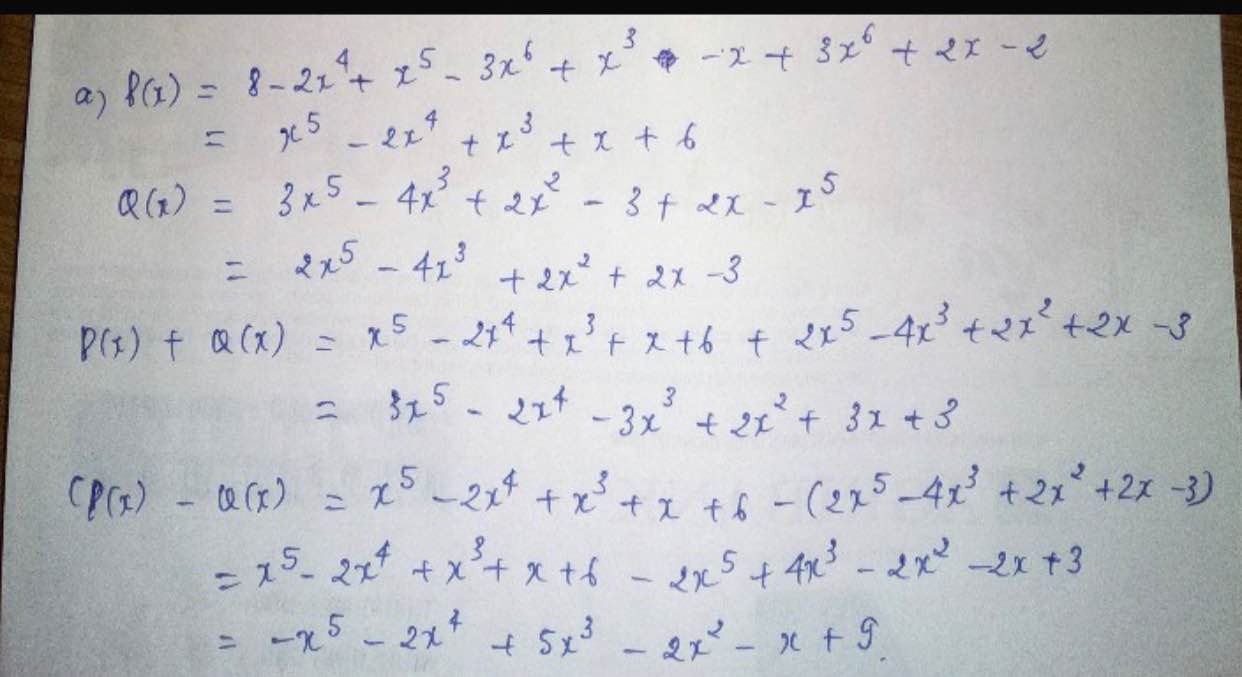

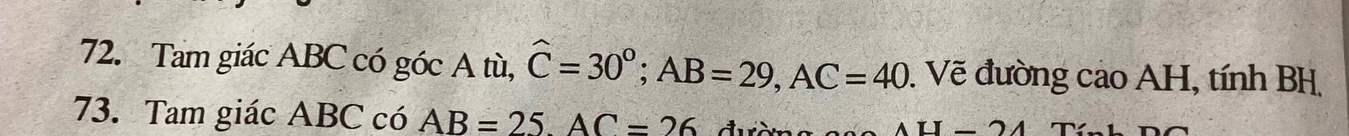 bài 72 giúp em 🥲🥲
bài 72 giúp em 🥲🥲
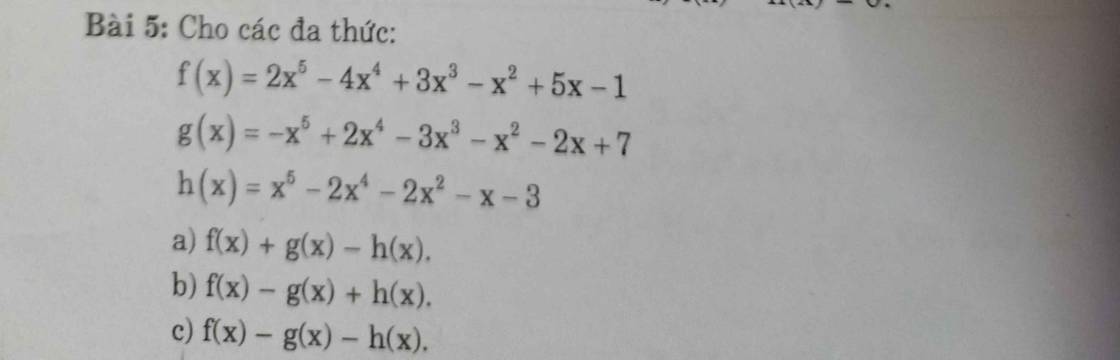


Bài 4:
a: \(x^4+7\ge7>0\forall x\)
Do đó: Đa thức này vô nghiệm
b: \(\left(x-1\right)^2+2\ge2>0\forall x\)
nên đa thức này vô nghiệm