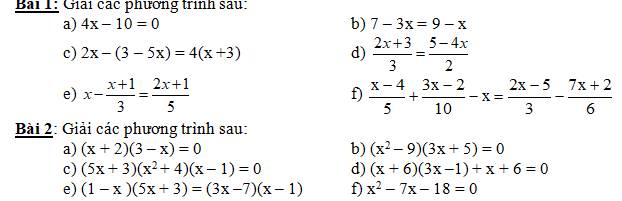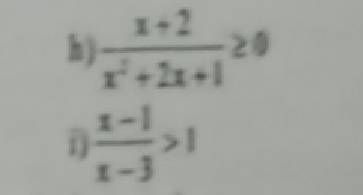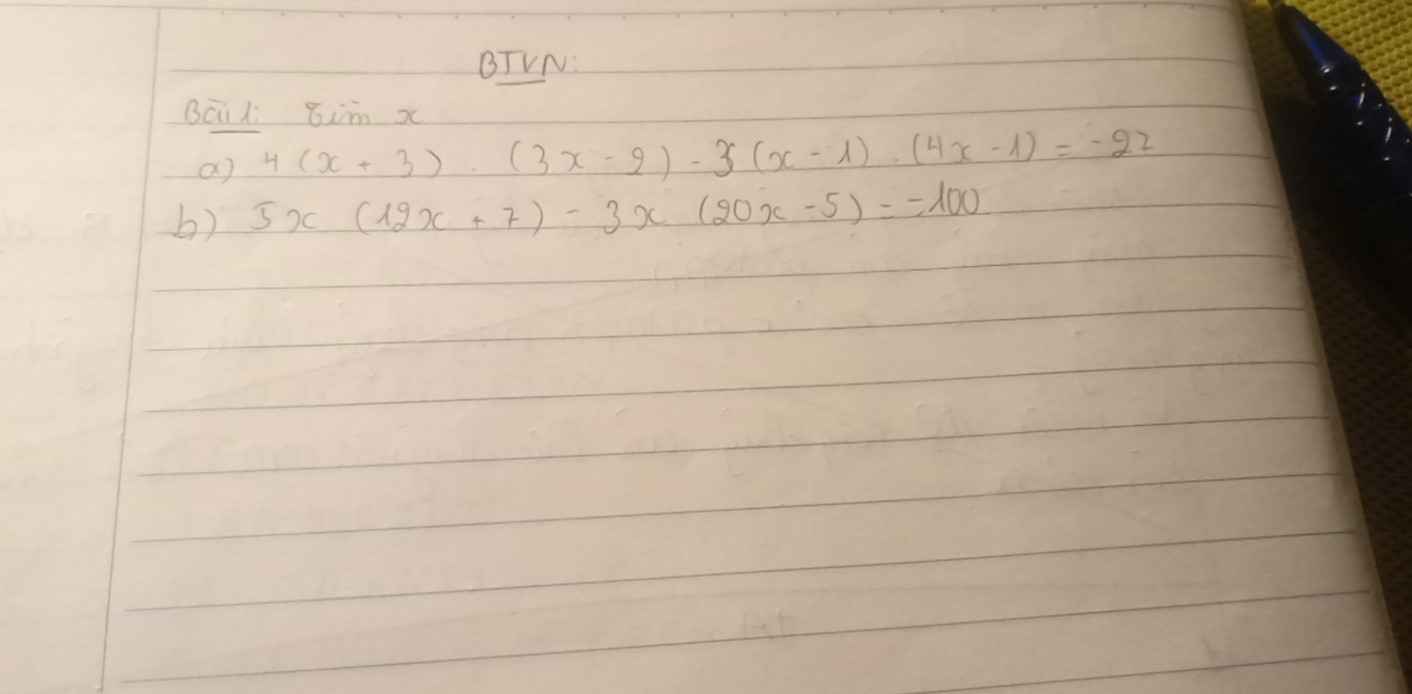Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1) a) 4x-10=0
4x=10
=>x=2,5
b) 7-3x=9-x
7-3x=-(3x-7)
-2x=2
=>x=-1
c) 2x-(3-5x)=4(x+3)
7x-3=4(x+3)
7x-3=4x+12
=>3x=15
=>x=5
d) 2x+3/3=5-4x/2
=>(2x+3)2=3(5-4x)
=>x=19/6

phương trình tích là phương trình có dạng A*B=0
=>A=0 hoặc B=0

h)\(\dfrac{x+2}{x^2+2x+1}\ge0\)
⇔\(\dfrac{x+2}{\left(x+1\right)^2}\ge0\)
⇔\(\dfrac{x+2}{\left(x+1\right)\left(x+1\right)}\ge\dfrac{0.\left(x+1\right)\left(x+1\right)}{\left(x+1\right)\left(x+1\right)}\)
⇒\(x+2\ge0\)
⇔\(x+2-2\ge0-2\)
⇔\(x\ge-2\)
i)\(\dfrac{x-1}{x-3}>1\)
⇔\(\dfrac{x-1}{x-3}>\dfrac{1.\left(x-3\right)}{1.x-3}\)
⇒\(x-1>x-3\)
⇔\(x-x>-3+1\)
⇔\(0x>-2\)

a: Xét tứ giác AMND có
AM//ND
AM=ND
Do đó: AMND là hình bình hành
Hình bình hành AMND có AM=AD(\(=\dfrac{AB}{2}\))
nên AMND là hình thoi
Xét tứ giác BMNC có
BM//NC
BM=NC
Do đó: BMNC là hình bình hành
Xét hình bình hành BMNC có \(MB=BC\left(=\dfrac{AB}{2}\right)\)
nên BMNC là hình thoi
b:
AMND là hình thoi
=>\(MN=AD=\dfrac{DC}{2}\)
Xét ΔDMC có
MN là đường trung tuyến
\(MN=\dfrac{DC}{2}\)
Do đó: ΔDMC vuông tại M
=>\(\widehat{DMC}=90^0\)
c: Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành
=>AN//CM

b: Ta có: \(5x\left(12x+7\right)-3x\left(20x-5\right)=-100\)
\(\Leftrightarrow60x^2+35x-60x^2+15x=-100\)
\(\Leftrightarrow50x=-100\)
hay x=-2

Bài 33:
a: \(x^2-3x+2=\left(x-2\right)\left(x-1\right)\)


a: Ta có: \(\left(x-1\right)\left(x^2+x+1\right)-x^3+2\)
\(=x^3-1-x^3+2\)
=1
b: ta có: \(\left(2x-y\right)\left(4x^2+2xy+y^2\right)-8x^3-5\)
\(=8x^3-y^3-8x^3-5\)
\(=-y^3-5\)
c: Ta có: \(\left(x+1\right)\left(x^2-x+1\right)-x^3+2\)
\(=x^3+1-x^3+2\)
=3
d: Ta có: \(\left(2x+y\right)\left(4x^2-2xy+y^2\right)-8x^3-5\)
\(=8x^3+y^3-8x^3-5\)
\(=y^3-5\)
a) \(\left(x-1\right)\left(x^2+x+1\right)-x^3+2=x^3-1-x^3+2=1\)
b) \(\left(2x-y\right)\left(4x^2+2xy+y^2\right)-8x^3-5=8x^3-y^3-8x^3-5=-y^3-5\)
c) \(\left(x+1\right)\left(x^2-x+1\right)-x^3+2=x^2+1-x^3+2=3\)
d) \(\left(2x+y\right)\left(4x^2-2xy+y^2\right)-8x^3-5=8x^3+y^3-8x^3-5=y^3-5\)
e) \(\left(3x+2\right)\left(9x^2-6x+4\right)-27x^3-7=27x^3+8-27x^3-7=1\)
f) \(\left(3x-2\right)\left(9x^2+6x+4\right)-27x^3-7=27x^3-8-27x^3-7=-15\)