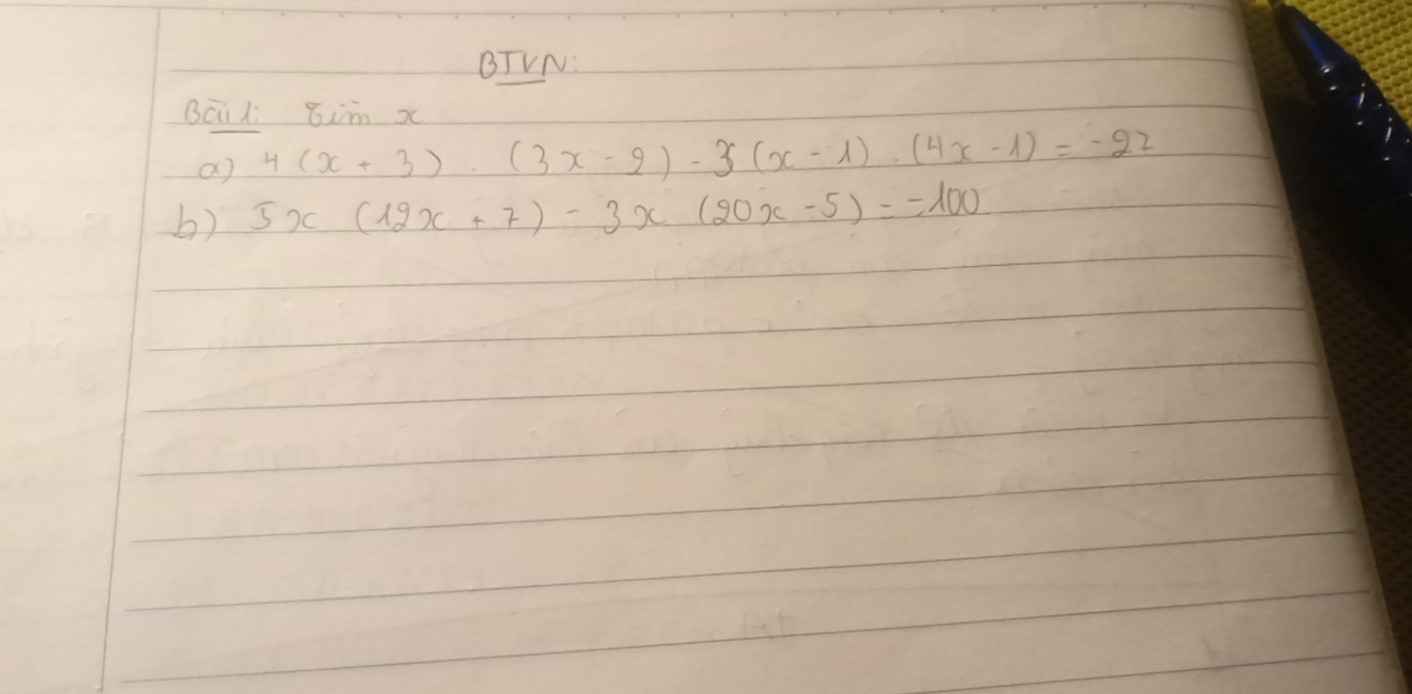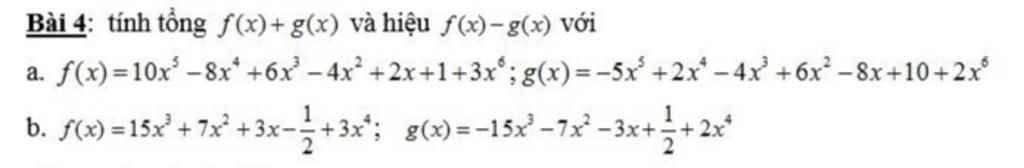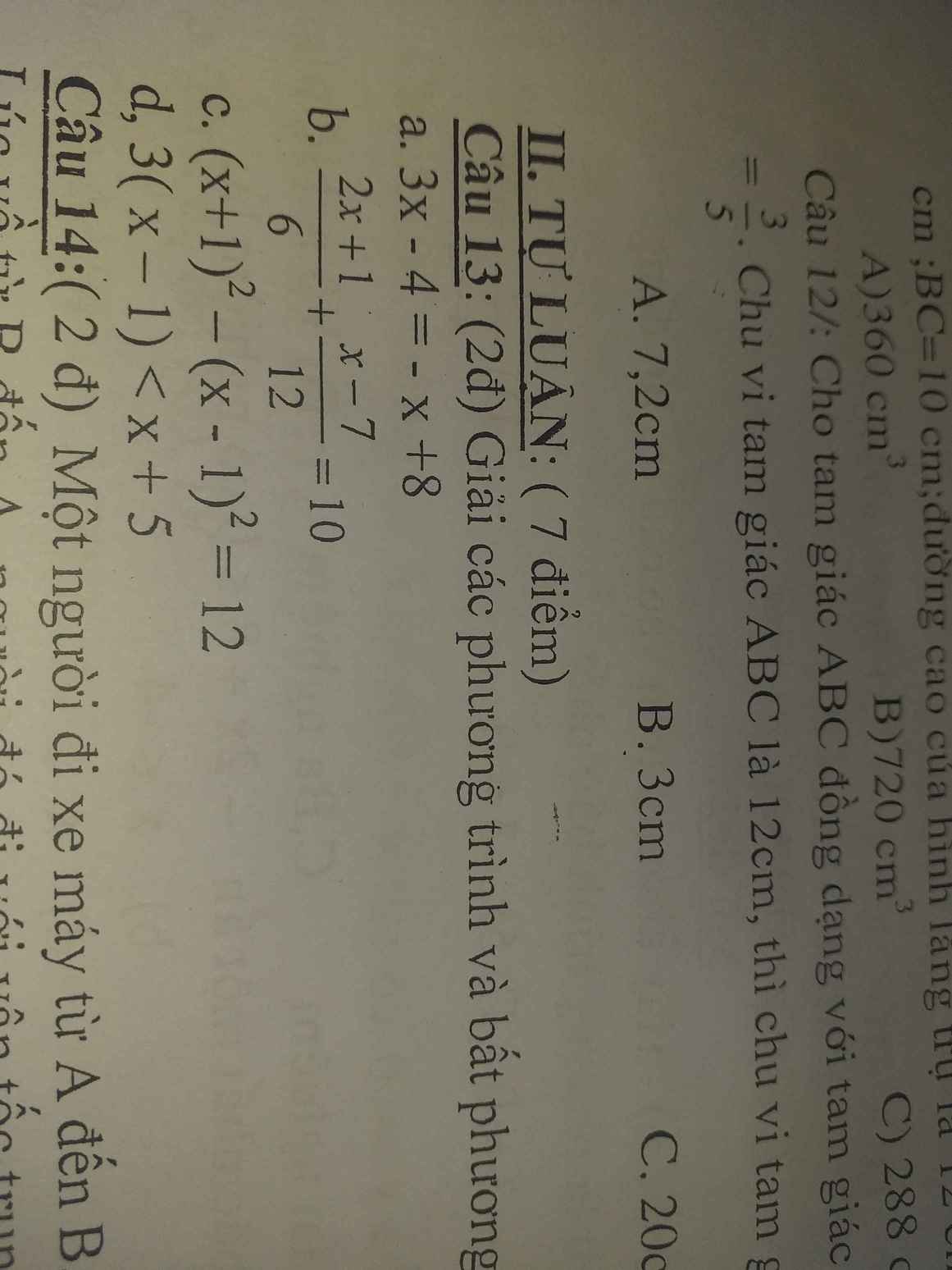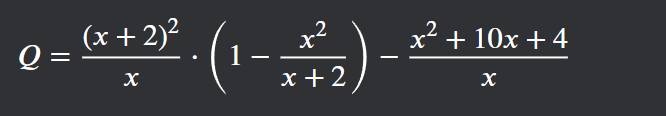K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
21 tháng 9 2021
b: Ta có: \(5x\left(12x+7\right)-3x\left(20x-5\right)=-100\)
\(\Leftrightarrow60x^2+35x-60x^2+15x=-100\)
\(\Leftrightarrow50x=-100\)
hay x=-2
24 tháng 6 2023
1: BC=căn 7,5^2+10^2=12,5cm
AH=7,5*10/12,5=6cm
góc ADH=góc AEH=góc DAE=90 độ
=>ADHE là hcn
=>DE=AH=6cm
2: ΔAHB vuông tại H có HD là đường cao
nên AD*AB=AH^2
ΔAHC vuông tại H có HElà đường cao
nên AE*AC=AH^2
=>AD*AB=AE*AC
3: ΔAHB vuông tại H có HD là đường cao
nên DH^2=AD*DB
4: AD=AH^2/AB=6^2/7,5=36/7,5=4,8cm
AE=AH^2/AC=6^2/10=3,6cm
S AED=1/2*3,6*4,8=8,64cm2
NM
1
5 tháng 2 2021
g, PT \(\Leftrightarrow\dfrac{x+24}{1996}+1+\dfrac{x+25}{1995}+1+\dfrac{x+26}{1994}+1+\dfrac{x+27}{1993}+1+\dfrac{x+2036}{4}-4=0\)
\(\Leftrightarrow\left(x+2020\right)\left(\dfrac{1}{1996}+\dfrac{1}{1995}+\dfrac{1}{1994}+\dfrac{1}{1993}+\dfrac{1}{4}\right)=0\)
\(\Leftrightarrow x+2020=0\)
\(\Leftrightarrow x=-2020\)
Vậy ...
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
27 tháng 7 2023
\(a,f\left(x\right)+g\left(x\right)\\ =10x^5-5x^5-8x^4+2x^4+6x^3-4x^3-4x^2+6x^2+2x-8x+1+10+3x^6+2x^6\\ =5x^6+5x^5-6x^4+2x^3+2x^2-6x+11\\ f\left(x\right)-g\left(x\right)\\ =3x^6-2x^6+10x^5+5x^5-8x^4-2x^4+6x^3+4x^3-4x^2-6x^2+2x+8x+1-10\\ =x^6+15x^5-10x^4+10x^3-10x^2+10x-9\)
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
27 tháng 7 2023
\(b,f\left(x\right) +g \left(x\right)=3x^4+2x^4+15x^3-15x^3+7x^2-7x^2+3x-3x-\dfrac{1}{2}+\dfrac{1}{2}=5x^4\\ f\left(x\right)-g\left(x\right)=3x^4-2x^4+15x^3+15x^3+7x^2+7x^2+3x+3x-\dfrac{1}{2}-\dfrac{1}{2}\\ =x^4+30x^3+14x^2+6x-1\)
3 tháng 5 2021
Em cần giúp câu nào hả em? Em nên chụp 1-2 ý cho 1 lần hỏi nhá, như thế mọi người sẽ dễ dàng giúp em hơn
PN
12 tháng 5 2021
13
a, \(3x-4=-x+8\)
\(< =>3x+x=8+4\)
\(< =>4x=12\)
\(< =>x=\frac{12}{4}=3\)
b, \(\frac{2x+1}{6}+\frac{x-7}{12}=10\)
\(< =>\frac{2\left(2x+1\right)}{12}+\frac{x-7}{12}=\frac{120}{12}\)
\(< =>4x+2+x-7=120\)
\(< =>5x=120+5=125\)
\(< =>x=\frac{125}{5}=\frac{5^3}{5}=5^2=25\)
T
1
H9
HT.Phong (9A5)
CTVHS
23 tháng 11 2023
a) \(Q=\dfrac{\left(x+2\right)^2}{x}\cdot\left(1-\dfrac{x^2}{x+2}\right)-\dfrac{x^2+10x+4}{x}\left(x\ne0;x\ne-2\right)\)
\(Q=\dfrac{\left(x+2\right)^2}{x}\cdot\dfrac{\left(x+2\right)-x^2}{x+2}-\dfrac{x^2+10x+4}{x}\)
\(Q=\dfrac{\left(x+2\right)^2}{x}\cdot\dfrac{-x^2+x+2}{x+2}-\dfrac{x^2+10x+4}{x}\)
\(Q=\dfrac{\left(x+2\right)\left(-x^2+x+2\right)}{x}-\dfrac{x^2+10x+4}{x}\)
\(Q=\dfrac{-x^3+x^2+2x-2x^2+2x+4-x^2-10x-4}{x}\)
\(Q=\dfrac{-x^3-2x^2-6x}{x}\)
\(Q=\dfrac{x\left(-x^2-2x-6\right)}{x}\)
\(Q=-x^2-2x-6\)
b) Ta có:
\(Q=-x^2-2x-6\)
\(Q=-\left(x^2+2x+6\right)\)
\(Q=-\left[\left(x^2+2x+1\right)+5\right]\)
\(Q=-\left(x+1\right)^2-5\)
Mà: \(-\left(x+1\right)^2\le0\forall x\)
\(\Rightarrow Q=-\left(x+1\right)^2-5\le-5\forall x\)
Dấu "=" xảy ra khi:
\(x+1=0\Rightarrow x=-1\)
Vậy: \(Q_{max}=-5\Leftrightarrow x=-1\)
LN
1
PL
1
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 12 2021
Tam giác ABC vuông tại A có AM là trung tuyến ứng với cạnh huyền
\(\Rightarrow AM=\dfrac{1}{2}BC\Rightarrow BC=2AM=50\left(m\right)\)
a. Áp dụng định lý Pitago:
\(AB=\sqrt{BC^2-AC^2}=30\left(m\right)\)
b. Kẻ \(MH\perp AC\Rightarrow MH||AB\) (cùng vuông góc AC)
Mà M là trung điểm BC \(\Rightarrow MH\) là đường trung bình tam giác ABC
\(\Rightarrow MH=\dfrac{1}{2}AB=15\left(m\right)\)
\(\Rightarrow S_{AMC}=\dfrac{1}{2}MH.AC=\dfrac{1}{2}.15.40=300\left(m^2\right)\)