
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


mình chỉ tóm tắt thôi nha, đừng trình bày theo mình!!!
m'on'=65(2 góc đối đỉnh)
ta có: 180-mon=m'on=15
=>m'on=mon'=15(2 góc đối đỉnh)
ta có: aob=a'ob'(2 góc đối đỉnh)(2 góc đỉnh tạo từ 2 đường thẳng cắt nhau,tạo thành 2 cặp tia đối nhau)
mà aob=60
=>a'ob'=60
vì ot là tia...của ot' nên
=> ot' là tia fân giác của a'ob'




\(B=\left(\frac{1}{2^2}-1\right).\left(\frac{1}{3^2}-1\right).\left(\frac{1}{4^2}-1\right)......\left(\frac{1}{100^2}-1\right).\)
\(B=\frac{-3}{2^2}\times\frac{-8}{3^2}\times\frac{-15}{4^2}\times.....\times\frac{-9999}{100^2}\)
\(B=-\left(\frac{3}{2^2}\times\frac{8}{3^2}\times.....\times\frac{9999}{100^2}\right)\)(vì A là tích của 99 thừa số âm nên kết quả là âm )
\(B=-\left(\frac{1.3}{2.2}\times\frac{2.4}{3.3}\times.....\times\frac{99.101}{100.100}\right)\)
\(B=-\left(\frac{1.2.3...99}{2.3.4.....100}\times\frac{3.4.5....101}{2.3.4....100}\right)\)
\(B=-\left(\frac{1}{100}\times\frac{101}{2}\right)\)
\(B=-\frac{101}{200}\)

Bài 1 :
a ) Áp dụng tính chất của dãy tỉ số bằng nhau ta có :
\(\frac{x}{12}=\frac{y}{-8}=\frac{x+y}{12+\left(-8\right)}=\frac{-48}{4}=-12.\)
\(\Rightarrow\hept{\begin{cases}\frac{x}{12}=-12\\\frac{y}{-8}=-12\end{cases}}\)\(\Rightarrow\hept{\begin{cases}x=-144\\y=96\end{cases}}\)
b ) Từ \(x\):\(\left(-7\right)\)= \(y\): \(10\)
\(\Rightarrow\)\(\frac{x}{-7}=\frac{y}{10}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{x}{-7}=\frac{y}{10}=\frac{y-x}{10-\left(-7\right)}=\frac{-34}{17}=-2\)
\(\Rightarrow\hept{\begin{cases}\frac{x}{-7}=-2\\\frac{y}{10}=-2\end{cases}}\)\(\Rightarrow\hept{\begin{cases}x=14\\y=-20\end{cases}}\)
c ) Áp dụng tính chất của dãy tỉ số bằng nhau ta có :
\(\frac{x}{15}=\frac{y}{-12}=\frac{2x}{30}=\frac{y}{-12}=\frac{2x+y}{30+\left(-12\right)}=\frac{-360}{18}=-20\)
\(\Rightarrow\hept{\begin{cases}\frac{x}{15}=-20\\\frac{y}{-12}=-20\end{cases}}\)\(\Rightarrow\hept{\begin{cases}x=-300\\y=240\end{cases}}\)
d ) Từ \(2x=-3y\)\(\Rightarrow\)\(\frac{x}{-3}=\frac{y}{2}\)
Áp dugj tính chất của dãy tỉ số bằng nhau ta có :
\(\frac{x}{-3}=\frac{y}{2}=\frac{x}{-3}=\frac{5y}{10}=\frac{x-5y}{-3-10}=\frac{-130}{-13}=10\)
\(\Rightarrow\hept{\begin{cases}\frac{x}{-3}=10\\\frac{y}{2}=10\end{cases}}\)\(\Rightarrow\hept{\begin{cases}x=-30\\y=20\end{cases}}\)
Bài 2 :
a ) Áp dụng tính chất của dãy tỉ số bằng nhau ta có :
\(\frac{x}{2}=\frac{y}{-3}=\frac{z}{5}=\frac{x+y-z}{2+\left(-3\right)-5}=\frac{-54}{-6}=9.\)
\(\Rightarrow\hept{\begin{cases}\frac{x}{2}=9\\\frac{y}{-3}=9\\\frac{z}{5}=9\end{cases}}\)\(\Rightarrow\hept{\begin{cases}x=18\\y=-27\\z=45\end{cases}}\)
b ) Áp dụng tính chất của dãy tỉ số bằng nhau ta có :
\(\frac{x}{4}=\frac{y}{-7}=\frac{z}{3}=\frac{x}{4}=\frac{2y}{-14}=\frac{z}{3}=\frac{x+2y-z}{4+\left(-14\right)-3}=\frac{-39}{-13}=3\)
\(\Rightarrow\hept{\begin{cases}\frac{x}{4}=3\\\frac{y}{-7}=3\\\frac{z}{3}=3\end{cases}}\)\(\Rightarrow\hept{\begin{cases}x=12\\y=-21\\z=9\end{cases}}\)


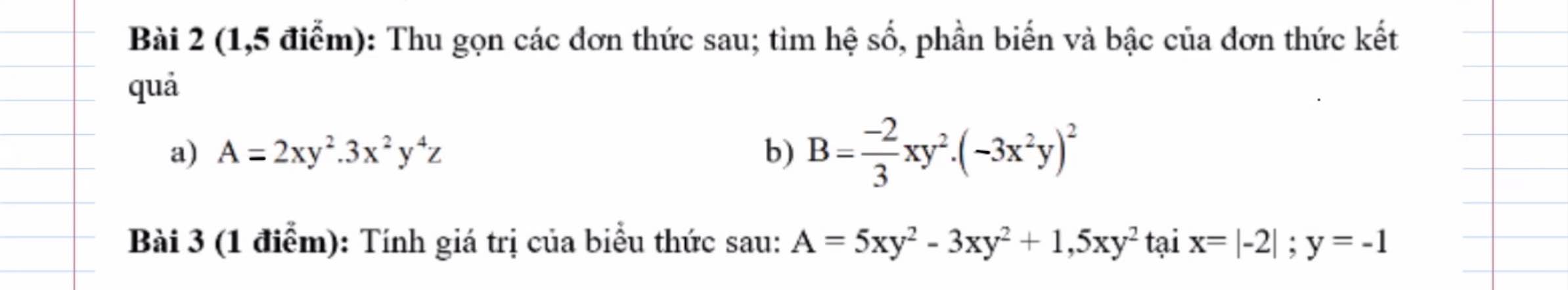

 GIÚP MÌNH VỚI Ạ MÌNH ĐANG CẦN GẤP Ạ MINH CẢM ƠN RẤT NHIỀU!!!!
GIÚP MÌNH VỚI Ạ MÌNH ĐANG CẦN GẤP Ạ MINH CẢM ƠN RẤT NHIỀU!!!! Giúp mình làm mấy câu tô màu vàng được ko ạ?Mình cảm ơn ạ!
Giúp mình làm mấy câu tô màu vàng được ko ạ?Mình cảm ơn ạ! Giải giúp mình bài 4, 5, 7 với ạ, mình cảm ơn trước ;-;
Giải giúp mình bài 4, 5, 7 với ạ, mình cảm ơn trước ;-; lm giúp mình câu 1b,c với ạ .Mình cảm ơn nhiều!
lm giúp mình câu 1b,c với ạ .Mình cảm ơn nhiều!






Bài 2 :
Bài 2 :
a, \(A=6x^3y^6z\)hệ số 6 ; biến x^3y^6z ; bậc 10
b, \(B=-\dfrac{2}{3}xy^2\left(9x^4y^2\right)=-6x^5y^4\)
hệ số -6 ; biến x^5y^4 ; bậc 9
Bài 3 :
\(A=3,5xy^2\) ta có \(x=\left|-2\right|=2;y=-1\)
Thay vào ta đc
A = 3,5 . 2 . 1 = 7
Này là đủ r đk bạn