K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
10 tháng 12 2021
2: \(A=x^2-10x+25-34=\left(x-5\right)^2-34\ge-34\forall x\)
Dấu '=' xảu ra khi x=5
10 tháng 12 2021
\(1,C=x^2+x-3\\ \Rightarrow C=\left(x^2+x+\dfrac{1}{4}\right)-\dfrac{13}{4}\\ \Rightarrow C=\left(x+\dfrac{1}{2}\right)^2-\dfrac{13}{4}\ge-\dfrac{13}{4}\)
dấu "=" xảy ra \(\Leftrightarrow x=-\dfrac{1}{2}\)
Vậy \(C_{min}=-\dfrac{13}{4}\Leftrightarrow x=-\dfrac{1}{2}\)
\(2,A=x^2-10x-9\\ \Rightarrow A=\left(x^2-10x+25\right)-34\\ \Rightarrow A=\left(x-5\right)^2-34\)
dấu "=" xảy ra \(\Leftrightarrow x=5\)
Vậy \(A_{min}=-34\Leftrightarrow x=5\)
PD
1
AH
Akai Haruma
Giáo viên
19 tháng 9 2021
Lời giải:
$A=11-5x-x^2=11-(x^2+5x)=17,25-(x^2+5x+2,5^2)=17,25-(x+2,5)^2$
Vì $(x+2,5)^2\geq 0$ với mọi $x$ nên $A=17,25-(x+2,5)^2\leq 17,25$
Vậy $A_{\max}=17,25$ khi $x+2,5=0\Leftrightarrow x=-2,5$
17 tháng 9 2021
3: Ta có: \(\left(x+3\right)\left(x^2-3x+9\right)-x\left(x-1\right)\left(x+1\right)=27\)
\(\Leftrightarrow x^3-27-x^3+x=27\)
hay x=54
UN
3
20 tháng 9 2021
Xét tứ giác ABCD có
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\)
\(\Leftrightarrow2\cdot\left(\widehat{A}+\widehat{D}\right)=360^0\)
\(\Leftrightarrow\widehat{A}+\widehat{D}=180^0\)
mà hai góc này là hai góc ở vị trí trong cùng phía
nên AB//CD
Xét tứ giác ABCD có AB//CD
nên ABCD là hình thang
mà \(\widehat{A}=\widehat{B}\)
nên ABCD là hình thang cân
GN
2
D
6 tháng 8 2021
- Ta có:
\(f\left(x\right)=\left(x+1\right)\left(x+2\right)\left(x+3\right)\left(x+4\right)+1\)
\(=\left(x+1\right)\left(x+4\right)\left(x+2\right)\left(x+3\right)+1\)
\(=\left(x^2+5x+4\right)\left(x^2+5x+6\right)+1\)
Đặt: \(\left(x^2+5x+5\right)=a\) ta được:
\(=\left(a-1\right)\left(a+1\right)+1\)
\(=a^2-1+1=a^2\)
Thay lại \(a=\left(x^2+5x+5\right)\) được:
\(\left(x^2+5x+5\right)^2\)
- Đối chiếu với \(\left(ax^2+bx+c\right)^2\)
Vậy \(a=1;b=5;c=5\)
P
2
NN
1
23 tháng 11 2021
XXét tứ giác AMDN có ^AMD=^MAN=^AND=90∞
⇒AMDN là hình chữ nhật
hcn AMDN có AD là phân giác góc A
⇒AMDN là hình vuông(dấu hiệu 3)
H
20 tháng 6 2023
B,
Hạng tử \(x^4\) : hệ số \(1\) , phần biến \(x^4\) ; Bậc : \(4\)
Hạng tử \(-4x^3y\) : hệ số \(-4\) ; phần biến : \(x^3y\) ; Bậc \(4\)
Hạng tử \(6x^2y\) : hệ số \(6\) ; phần biến : \(x^2y\) ; Bậc : \(3\)
Hạng tử \(-4xy\) : hệ số \(-4\) ; phần biến : \(xy\) ; bậc \(2\)
Hạng tử \(y\) : hệ số \(1\) ; phần biến : \(y\) ; bậc 1
C,
Hạng tử \(2023x^{2024}y^{2025}\) : hệ số \(2023\) ; phần biến \(x^{2024}y^{2025}\) ; bậc : \(4049\)
Hạng tử \(-\dfrac{1}{2026}yz^{2027}\) : hệ số \(-\dfrac{1}{2026}\) ; phần biến : \(yz^{2027}\) ; bậc : \(2028\)
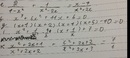
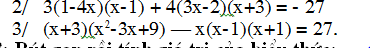
a) đkxđ: \(x\ne\pm2\)
Ta có: \(\frac{x+2}{x-2}-\frac{x-2}{x+2}=\frac{4}{x^2-4}\)
\(\Leftrightarrow\frac{\left(x+2\right)^2-\left(x-2\right)^2}{\left(x-2\right)\left(x+2\right)}=\frac{4}{\left(x-2\right)\left(x+2\right)}\)
\(\Rightarrow8x=4\)\(\Rightarrow x=\frac{1}{2}\)
b) đkxđ: \(x\ne\left\{1;-3\right\}\)
PT \(\Leftrightarrow\frac{\left(x+1\right)\left(x+3\right)-\left(x+2\right)\left(x-1\right)+4}{\left(x-1\right)\left(x+3\right)}=0\)
\(\Rightarrow x^2+4x+3-x^2-x+2+4=0\)
\(\Leftrightarrow3x+10=0\Rightarrow x=-\frac{10}{3}\)
c) đkxđ: \(x\ne\left\{0;-1\right\}\)
\(PT\Leftrightarrow\frac{\left(x-1\right)\left(x+1\right)+1-2x}{x\left(x+1\right)}=\frac{x}{x\left(x+1\right)}\)
\(\Rightarrow x^2-1+1-2x=x\)
\(\Leftrightarrow x^2-3x=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=0\left(ktm\right)\\x=3\left(tm\right)\end{cases}}\)
d) đkxđ: \(x\ne\left\{1;5\right\}\)
\(PT\Leftrightarrow\frac{x-1-3}{\left(x-1\right)\left(x-5\right)}=\frac{5\left(x-5\right)}{\left(x-1\right)\left(x-5\right)}\)
\(\Rightarrow x-4=5x-25\)
\(\Leftrightarrow4x=21\Rightarrow x=\frac{21}{4}\)
e) đkxđ: \(x\ne\left\{0;-2;2\right\}\)
\(PT\Leftrightarrow\frac{-2x+x+2}{x\left(x-2\right)\left(x+2\right)}=\frac{\left(x-4\right)\left(x-2\right)}{x\left(x-2\right)\left(x+2\right)}\)
\(\Rightarrow-x+2=x^2-6x+8\)
\(\Leftrightarrow x^2-5x+6=0\Leftrightarrow\left(x-2\right)\left(x-3\right)=0\Rightarrow\orbr{\begin{cases}x=2\\x=3\end{cases}}\)