
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 6:
Phương trình hoành độ giao điểm là:
\(ax^2+4x+4=0\)
\(\text{Δ}=16-16a\)
Để (P) tiếp xúc với (d) thì 16-16a=0
hay a=1

Bài 1:
a) Ta có: \(B=\dfrac{x}{\sqrt{x}-1}-\dfrac{2x-\sqrt{x}}{x-\sqrt{x}}\)
\(=\dfrac{x}{\sqrt{x}-1}-\dfrac{\sqrt{x}\left(2\sqrt{x}-1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}\)
\(=\dfrac{x-2\sqrt{x}+1}{\sqrt{x}-1}\)
\(=\dfrac{\left(\sqrt{x}-1\right)^2}{\sqrt{x}-1}=\sqrt{x}-1\)

ĐK: \(x>0;x\ne1\)
\(C=\left(\sqrt{x}-\dfrac{1}{\sqrt{x}}\right):\left(\dfrac{\sqrt{x}-1}{\sqrt{x}}+\dfrac{1-\sqrt{x}}{x+\sqrt{x}}\right)\)
\(=\dfrac{x-1}{\sqrt{x}}:\left(\dfrac{\left(\sqrt{x}-1\right)^2\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)\left(\sqrt{x+1}\right)}-\dfrac{\left(\sqrt{x}-1\right)^2}{\sqrt{x}\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\right)\)
\(=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}}:\dfrac{\left(\sqrt{x}-1\right)^2\left(\sqrt{x}+1\right)-\left(\sqrt{x}-1\right)^2}{\sqrt{x}\left(\sqrt{x}-1\right)\left(\sqrt{x+1}\right)}\)
\(=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}}.\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)^2\left(\sqrt{x}+1\right)-\left(\sqrt{x}-1\right)^2}\)
\(=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)-\left(\sqrt{x}-1\right)}\)
\(=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)^2}{\sqrt{x}\left(\sqrt{x}-1\right)}\)
\(=\dfrac{\left(\sqrt{x}+1\right)^2}{\sqrt{x}}=\sqrt{x}+\dfrac{1}{\sqrt{x}}+2\ge2\sqrt{\sqrt{x}.\dfrac{1}{\sqrt{x}}}+2=4\)
Đẳng thức không xảy ra nên \(C>4\).

1: Thay x=36 vào A, ta được:
\(A=\dfrac{6+4}{6+2}=\dfrac{10}{8}=\dfrac{5}{4}\)
2: Ta có: \(B=\left(\dfrac{\sqrt{x}}{\sqrt{x}+4}+\dfrac{4}{\sqrt{x}-4}\right):\dfrac{x+16}{\sqrt{x}+2}\)
\(=\dfrac{x-4\sqrt{x}+4\sqrt{x}+16}{\left(\sqrt{x}+4\right)\left(\sqrt{x}-4\right)}\cdot\dfrac{\sqrt{x}+2}{x+16}\)
\(=\dfrac{\sqrt{x}+12}{x-16}\)

a: Xét (O) có
ΔAIB nội tiếp
AB là đường kính
=>ΔAIB vuông tại I
Xét ΔBAE có
BI vừa là đường cao, vừa là phân giác
nên ΔBAE cân tại B
b: Xét (O) có
ΔACB nội tiếp
AB là đường kính
=>ΔBCA vuông tại C
Xét ΔEAB co
BI.AC là các đường cao
BI cắt AC tại K
=>K là trực tâm
=>EK vuông góc với AB

\(a,VT=\dfrac{1+cos\alpha}{1-cos\alpha}-\dfrac{1-cos\alpha}{1+cos\alpha}=\dfrac{\left(1+cos\alpha\right)^2-\left(1-cos\alpha\right)^2}{1^2-cos\alpha^2}\\ =\dfrac{1+2cos\alpha+cos^2\alpha-1+2cos\alpha-cos^2\alpha}{sin^2\alpha}\\ =\dfrac{4cos\alpha}{sin^2\alpha}\\ =4\left(\dfrac{cos\alpha}{sin\alpha}:\dfrac{sin^2\alpha}{sin\alpha}\right)\\ =\dfrac{4cot\alpha}{sin\alpha}=VP\left(dpcm\right)\)

a) \(A=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}+\dfrac{2}{x-\sqrt{x}}\right):\dfrac{1}{\sqrt{x}-1}\left(đk:x>0,x\ne1\right)\)
\(=\dfrac{x+2}{\sqrt{x}\left(\sqrt{x}-1\right)}.\left(\sqrt{x}-1\right)=\dfrac{x+2}{\sqrt{x}}\)
a: ĐKXĐ: \(\left\{{}\begin{matrix}x>0\\x\ne1\end{matrix}\right.\)
Ta có: \(A=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}+\dfrac{2}{x-\sqrt{x}}\right):\dfrac{1}{\sqrt{x}-1}\)
\(=\dfrac{x+2}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\dfrac{\sqrt{x}-1}{1}\)
\(=\dfrac{x+2}{\sqrt{x}}\)



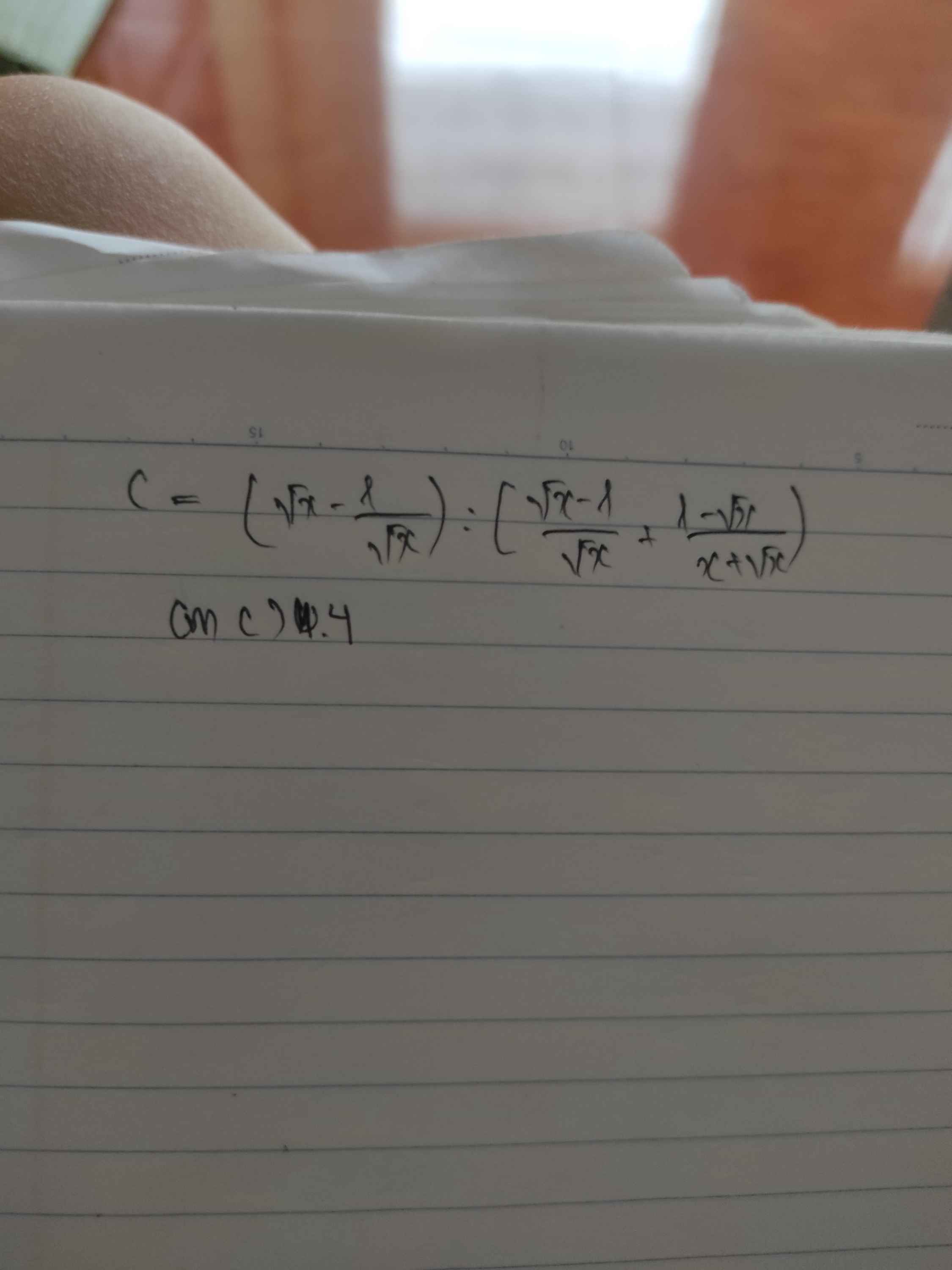


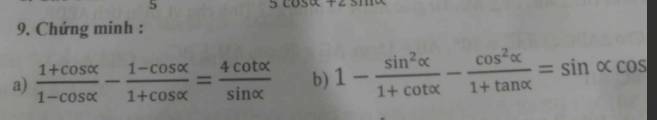 chứng minh theo kiểu vt=... = vp(dpcm) giúp mình với
chứng minh theo kiểu vt=... = vp(dpcm) giúp mình với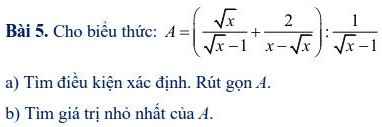

ĐKXĐ: \(x+1\ne0\)\(\Rightarrow x\ne-1\)
Ta có:\(\left(\frac{x+2}{x+1}\right)^2-\frac{1}{x+1}-3=0\)
<=>\(\frac{x^2+4x+4}{x^2+2x+1}-\frac{x+1}{x^2+2x+1}-\frac{3\left(x^2+2x+1\right)}{x^2+2x+1}=0\)
<=>\(x^2+4x+4-x-1-3\left(x^2+2x+1\right)=0\)
<=>\(x^2+4x+4-x-1-3x^2-6x-3=0\)
<=>\(-2x^2-3x=0\)
<=>\(-x\left(2x+3\right)=0\)
<=>\(\orbr{\begin{cases}-x=0\\2x+3=0\end{cases}}\)
<=>\(\orbr{\begin{cases}x=0\left(TM\right)\\x=\frac{-3}{2}\left(TM\right)\end{cases}}\)
Vậy phương trình có 2 nghiệm x=0 hoặc x=\(\frac{-3}{2}\)