K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
14 tháng 10 2021
Bài 9:
a: \(2^{195}=8^{65}\)
\(3^{130}=9^{65}\)
mà 8<9
nên \(2^{195}< 3^{130}\)
CN
7
8 tháng 3 2022
Câu 4:
a: Xét ΔBAE vuông tại A và ΔBHE vuông tại H có
BE chung
\(\widehat{ABE}=\widehat{HBE}\)
Do đó: ΔBAE=ΔBHE
Suy ra: BA=BH và EA=EH
b: Xét ΔAEK vuông tại A và ΔHEC vuông tại H có
EA=EH
\(\widehat{AEK}=\widehat{HEC}\)
Do đó: ΔAEK=ΔHEC
Suy ra: AK=HC
Ta có: BA+AK=BK
BH+HC=BC
mà BA=BH
và AK=HC
nên BK=BC
hay ΔBKC cân tại B
c: \(AC=\sqrt{BC^2-AB^2}=8\left(cm\right)\)
DN
2
24 tháng 1 2022
Câu 1: A
Câu 2: B
Câu 3: D
Câu 4: A
Câu 5: C
Câu 6: B
Câu 7: A
Câu 8: C
24 tháng 1 2022
Câu 1 : A
Câu 2 : B
Câu 3 : D
Câu 4 : A
Câu 5 : C
Câu 6 : B
Câu 7 : A
Câu 8 : C
HT
NT
2
NT
4
LM
Lê Minh Vũ
CTVHS
14 tháng 6 2023
\(2.16\ge2^n>4\)
\(2.2^4\ge2^n>2^2\)
\(2^5\ge2^n>2^2\)
=> \(n\in\left\{3,4,5\right\}\)
Vậy: \(n\in\left\{3,4,5\right\}\)
15 tháng 8 2016
\(-\frac{2}{3}=\frac{10}{-15}=-\frac{10}{15}\)
\(\frac{4}{-5}=\frac{12}{-15}=-\frac{12}{15}\)
\(V\text{ì}-\frac{10}{15}>-\frac{12}{15}\)
Nên \(-\frac{2}{3}>-\frac{4}{5}\)
15 tháng 8 2016
Ta có:
\(-\frac{2}{3}=\frac{4}{-6}\)
Vì \(\frac{4}{-6}>\frac{3}{-5}\Rightarrow\frac{-2}{3}>\frac{3}{-5}\)
Vậy \(\frac{-2}{3}>\frac{4}{-5}\)
?
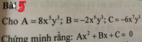
Bạn phải nói xem bạn cần giúp cái gì người ta mới giúp được chứ :3