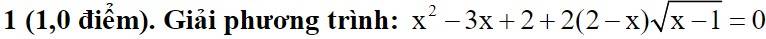Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Mình không thấy câu nào cả thì giúp kiểu gì lỗi ảnh hay sao ý

b) \(\sqrt{x^2}=\left|-8\right|\)
\(\Rightarrow\left|x\right|=8\)
\(\Rightarrow\left[{}\begin{matrix}x=8\\x=-8\end{matrix}\right.\)
d) \(\sqrt{9x^2}=\left|-12\right|\)
\(\Rightarrow\sqrt{\left(3x\right)^2}=12\)
\(\Rightarrow\left|3x\right|=12\)
\(\Rightarrow\left[{}\begin{matrix}3x=12\\3x=-12\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{12}{3}\\x=-\dfrac{12}{3}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=4\\x=-4\end{matrix}\right.\)

ĐKXĐ: \(x+2y\ne0\)
\(\left\{{}\begin{matrix}x-\dfrac{1}{x+2y}=\dfrac{7}{4}\\-\dfrac{5}{2}x+2+\dfrac{4}{x+2y}=-2\end{matrix}\right.\)
Đặt \(\dfrac{1}{x+2y}=z\) ta được hệ:
\(\left\{{}\begin{matrix}x-z=\dfrac{7}{4}\\-\dfrac{5}{2}x+4z=-4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=2\\z=\dfrac{1}{4}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=2\\\dfrac{1}{x+2y}=\dfrac{1}{4}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=2\\x+2y=4\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)

ĐKXĐ: \(\left\{{}\begin{matrix}2x-3>=0\\x+1>=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=\dfrac{3}{2}\\x>=-1\end{matrix}\right.\)
=>\(x>=\dfrac{3}{2}\)
\(\sqrt{2x-3}-\sqrt{x+1}=x-4\)
=>\(\dfrac{2x-3-x-1}{\sqrt{2x-3}+\sqrt{x+1}}-\left(x-4\right)=0\)
=>\(\left(x-4\right)\left(\dfrac{1}{\sqrt{2x-3}+\sqrt{x+1}}-1\right)=0\)
=>x-4=0
=>x=4(nhận)

Gọi số xe dự định tham gia chở hàng là x (xe) với x>4, x nguyên dương
Mỗi xe dự định chở khối lượng hàng là: \(\dfrac{20}{x}\) (tấn)
Số xe thực tế tham gia chở hàng là: \(x-4\) (xe)
Thực tế mỗi xe phải chở số hàng là: \(\dfrac{20}{x-4}\) (tấn)
Do thực tế mỗi xe phải chở nhiều hơn dự định là 5/6 tấn hàng nên ta có pt:
\(\dfrac{20}{x-4}-\dfrac{20}{x}=\dfrac{5}{6}\)
\(\Rightarrow24x-24\left(x-4\right)=x\left(x-4\right)\)
\(\Leftrightarrow x^2-4x-96=0\)
\(\Rightarrow\left[{}\begin{matrix}x=12\\x=-8\left(loại\right)\end{matrix}\right.\)
Vậy thực tế có \(12-4=8\) xe tham gia vận chuyển

M A O B E F H K P Q
a/
Ta có
AE = HE; BF = HF (2 tiếp tuyến cùng xp từ 1 điểm ngoài hình tròn thì khoảng cách từ điểm đó đến 2 tiếp điểm bằng nhau)
=> AE + BF = HE + HF = EF (dpcm)
b/ Gọi P; K; Q lần lượt là giao của OE; OM; OF với (O)
Ta có
sđ cung PA = sđ cung PH (Hai tiếp tuyến cùng xp từ 1 điểm ngoài hình tròn thì đường nối điểm đó với tâm chia đôi cung chắn bởi 2 tiếp điểm)
sđ cung QB = sđ cung QH (lý do như trên)
=> sđ cung PH + sđ cung QH = sđ cung PA + sđ cung QB
=> sđ cung APH = sđ cung BQH
Mà sđ cung APH + sđ cung BQH = sđ cung AKB
=> sđ cung APH = sđ cung BQH = \(\dfrac{sđcungAKB}{2}\) (1)
Ta có
sđ cung KA = sđ cung KB (Hai tiếp tuyến cùng xp từ 1 điểm ngoài hình tròn thì đường nối điểm đó với tâm chia đôi cung chắn bởi 2 tiếp điểm)
Mà sđ cung KA + sđ cung KB = sđ cung AKB
=> sđ cung KA = sđ cung KB = \(\dfrac{sđcungAKB}{2}\) (2)
Ta có
\(sđ\widehat{MOA}=sđcungKA=\dfrac{sđcungAKB}{2}\) (góc ở tâm đường tròn) (3)
\(sđ\widehat{FOE}=sđcungPHQ=sđcungPH+sđcungQH=\dfrac{sđcungAKB}{2}\) (góc ở tâm đường tròn) (4)
Từ (1) (2) (3) (4) \(\Rightarrow\widehat{MOA}=\widehat{FOE}\)

\(x^2+3x+2+2\left(2-x\right)\sqrt{x-1}=0\left(x\ge1\right)\)
\(\Leftrightarrow x^2-x-2x+2-2\left(x-2\right)\sqrt{x-1}=0\)
\(\Leftrightarrow x\left(x-1\right)-2\left(x-1\right)-2\left(x-2\right)\sqrt{x-1}=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-2\right)-2\left(x-2\right)\sqrt{x-1}=0\)
\(\Leftrightarrow\left(x-2\right)\sqrt{x-1}\left(\sqrt{x-1}-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\\sqrt{x-1}=0\\\sqrt{x-1}-2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\left(tm\right)\\x-1=0\\\sqrt{x-1}=2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\left(tm\right)\\x=1\left(tm\right)\\x-1=4\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=1\\x=5\end{matrix}\right.\left(tm\right)\)
Vậy: \(x\in\left\{1;2;5\right\}\)

k/ \(\sqrt{8+\sqrt{60}}-\sqrt{\dfrac{2}{\sqrt{15}+4}}=\sqrt{\left(\sqrt{3}+\sqrt{5}\right)^2}-\sqrt{\left(\sqrt{5}-\sqrt{3}\right)^2}=\sqrt{3}+\sqrt{5}-\sqrt{5}+\sqrt{3}=2\sqrt{3}\)
l/ \(\sqrt{\dfrac{3\sqrt{5}-1}{2\sqrt{5}+3}}=\sqrt{\dfrac{\left(3\sqrt{5}-1\right)\left(2\sqrt{5}-3\right)}{11}}=\sqrt{\dfrac{33-11\sqrt{5}}{11}}=\sqrt{3-\sqrt{5}}\)
\(\sqrt{\dfrac{\sqrt{5}+11}{7-2\sqrt{5}}}=\sqrt{\dfrac{\left(\sqrt{5}+11\right)\left(7+2\sqrt{5}\right)}{29}}=\sqrt{\dfrac{87+29\sqrt{5}}{29}}=\sqrt{3+\sqrt{5}}\)
\(\sqrt{\dfrac{3\sqrt{5}-1}{2\sqrt{5}+3}}-\sqrt{\dfrac{\sqrt{5}+11}{7-2\sqrt{5}}}=\sqrt{3-\sqrt{5}}-\sqrt{3+\sqrt{5}}=\dfrac{-2\sqrt{5}}{\sqrt{3-\sqrt{5}}+\sqrt{3+\sqrt{5}}}\)

Bài 5:
a: Xét (O) có
CA là tiếp tuyến
CM là tiếp tuyến
Do đó: CA=CM
Xét (O) có
DM là tiếp tuyến
DB là tiếp tuyến
Do đó: DM=DB
CD=CM+MD
nên CD=CA+DB
b: Ta có: CA=CM
OA=OM
Do đó: CO là đường trung trực của AM
=>CO vuông góc với AM tại P
Ta có: DM=DB
OM=OB
Do đó: OD là đường trung trực của MB
=>OD vuông góc với MB tại Q
Xét (O) có
ΔAMB nội tiếp
AB là đường kính
Do đó: ΔAMB vuông tại M
Xét tứ giác MPOQ có \(\widehat{MPO}=\widehat{MQO}=\widehat{PMQ}=90^0\)
nên MPOQ là hình chữ nhật