
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



bạn tự vẽ hình nha
giải
a) K là trung điểm EM
H là trung điểm ED
=> KH là đường trung bình của \(\Delta\) EMD ( đpcm)
b) KH là đường trung bình \(\Delta EMD\)
\(\Rightarrow\) KH = \(\dfrac{1}{2}MD\)
\(\Rightarrow MD=2.KH\Rightarrow MD=2.20=40\) ( cm)
c) KH là đường trung bình \(\Delta EMD\)
\(\Rightarrow\) KH // MD (1)
\(\Delta EMD\) cân \(\Rightarrow\) \(\widehat{M}=\widehat{D}\) (2)
từ (1) và (2) tứ giác KHDM là hình thang cân ( đpcm )
a: Xét ΔEMD có
K là trung điểm của EM
H là trung điểm của ED
Do đó: KH là đường trung bình của ΔEMD
b: \(MD=2\cdot KH=2\cdot20=40\left(cm\right)\)
c: Xét tứ giác MKHD có HK//MD
nên MKHD là hình thang
mà \(\widehat{M}=\widehat{D}\)
nên MKHD là hình thang cân

Bài 2:
a: Xét tứ giác AMND có
AM//ND
AM=ND
Do đó: AMND là hình bình hành
b: Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành

-Gọi x (đồng) là giá niêm yết của chai nước rửa tay sát khuẩn (x>0).
a là số chai nước rửa tay nhiều nhất có thể mua đc sau khi khuyến mãi
(a là số tự nhiên khác 0).
-Số tiền An mang theo là: \(9x\left(đồng\right)\)
-Giá tiền của chai nước rửa tay sát khuẩn sau khi khuyến mãi là:
\(\left[x.\left(100\%-20\%\right)\right]=\dfrac{4}{5}x\left(đồng\right)\)
-Từ đề bài ta có BĐT sau:
\(9x\ge x+a.\dfrac{4}{5}x\).
\(\Leftrightarrow9x-x-a.\dfrac{4}{5}x\ge0\)
\(\Leftrightarrow\left(8-\dfrac{4}{5}a\right)x\ge0\)
Vì \(x>0\) nên BĐT đã cho tương đương:
\(8-\dfrac{4}{5}a\ge0\)
\(\Leftrightarrow a\le10\).
Mà a là số chai nước rửa tay nhiều nhất có thể mua đc sau khi khuyến mãi.
\(\Rightarrow a=10\)
-Vậy bạn An có thể mua được 10 chai nước theo chương trình khuyến mãi trên.




\(X^2-X+Y^2+Y+\frac{1}{2}=0\)
<=> \(\left(X^2-2X\frac{1}{2}+\frac{1}{4}\right)+\left(Y^2+2Y\frac{1}{2}+\frac{1}{4}\right)=0\)
<=>\(\left(X-\frac{1}{2}\right)^2+\left(Y+\frac{1}{2}\right)^2=0\)
Vì \(\left(X-\frac{1}{2}\right)^2\ge0\forall X\) , ,\(\left(Y+\frac{1}{2}\right)^2\ge0\forall Y\)
=> \(VT\ge0\forall X;Y\)
mà VT = 0
Từ 2 điều trên => \(\hept{\begin{cases}\left(X-\frac{1}{2}\right)^2=0\\\left(Y+\frac{1}{2}\right)^2=0\end{cases}}\)
<=>\(\hept{\begin{cases}X-\frac{1}{2}=0\\Y+\frac{1}{2}=0\end{cases}}\)
<=>\(\hept{\begin{cases}X=\frac{1}{2}\\Y=-\frac{1}{2}\end{cases}}\)
kết luận:
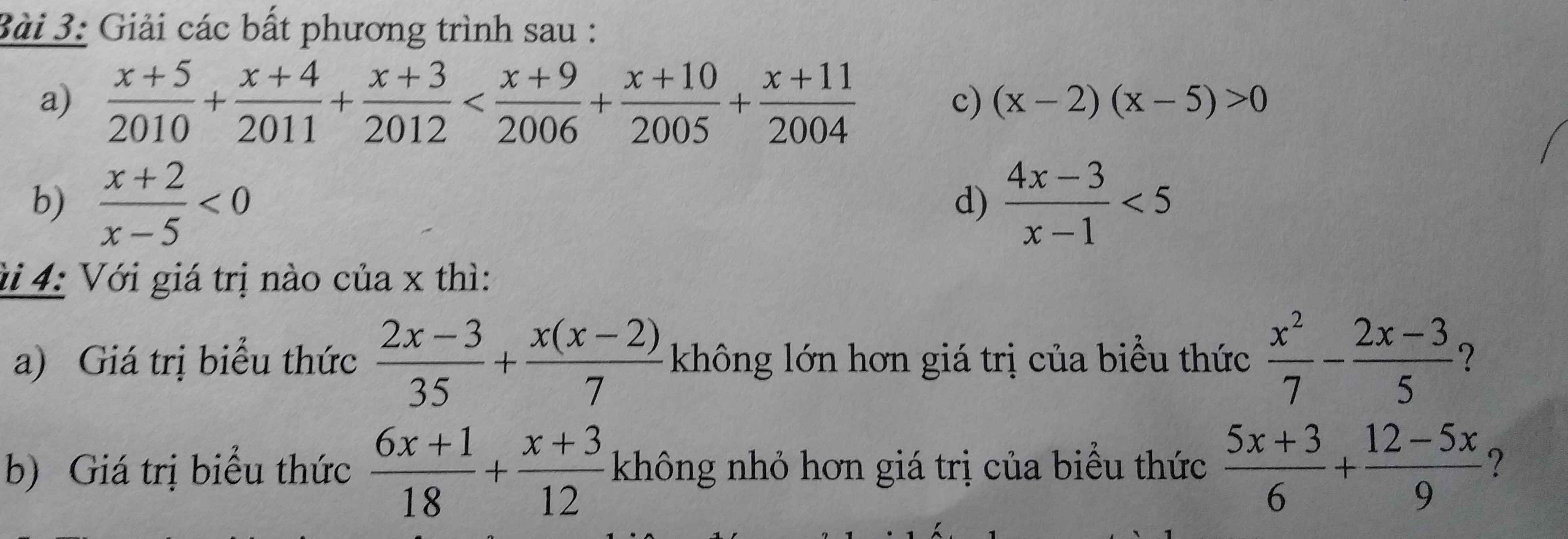





3
a: =>\(\left(\dfrac{x+5}{2010}+1\right)+\left(\dfrac{x+4}{2011}+1\right)+\left(\dfrac{x+3}{2012}+1\right)< \left(\dfrac{x+9}{2006}+1\right)+\left(\dfrac{x+10}{2005}+1\right)+\left(\dfrac{x+11}{2004}+1\right)\)
=>x+2015<0
=>x<-2015
b: =>x+2>0 và x-5<0
=>-2<x<5
c: =>x-5>0 hoặc x-2<0
=>x<2 hoặc x>5
d: =>(4x-3-5x+5)/(x-1)<0
=>(-x+2)/(x-1)<0
=>(x-2)/(x-1)>0
=>x>2 hoặc x<1