NB
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
5 tháng 2 2022
Bài 4:
a: Xét ΔBDC vuông tại D có \(BC^2=BD^2+DC^2\)
nên BC=10(cm)
b: Xét ΔABD vuông tại D và ΔACE vuông tại E có
AB=AC
\(\widehat{EAC}\) chung
Do đó: ΔABD=ΔACE
c: Ta có: ΔABD=ΔACE
nên AD=AE
hay ΔADE cân tại A
Xét ΔABC có
AE/AB=AD/AC
nên DE//BC
d: Xét ΔDBC vuông tại D và ΔDKC vuông tại D có
DB=DK
DC chung
Do đó: ΔDBC=ΔDKC
Suy ra: \(\widehat{DBC}=\widehat{DKC}\left(1\right)\)
Xét ΔEBC vuông tại E và ΔDCB vuông tại D có
BC chung
EC=DB
Do đó: ΔEBC=ΔDCB
Suy ra: \(\widehat{ECB}=\widehat{DBC}\left(2\right)\)
Từ (1) và (2) suy ra \(\widehat{ECB}=\widehat{DKC}\)
TV
0
8 tháng 11 2019
\(B=|2014-2x|+|2016-2x|\)
\(=|2014-2x|+|2x-2016|\ge|2014-2x+2x-2016|\)
Hay \(B\ge2\)
Dấu"="xảy ra \(\Leftrightarrow\left(2014-2x\right)\left(2x-2016\right)\ge0\)
\(\Leftrightarrow\hept{\begin{cases}2014-2x\ge0\\2x-2016\ge0\end{cases}}\)hoặc \(\hept{\begin{cases}2014-2x< 0\\2x-2016< 0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}2x\le2014\\2x\ge2016\end{cases}\left(loai\right)}\)hoặc\(\hept{\begin{cases}2x>2014\\2x< 2016\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x>1007\\x< 1008\end{cases}}\)
\(\Leftrightarrow1007< x< 1008\)
Vậy \(B_{min}=2\)\(\Leftrightarrow1007< x< 1008\)
IC
1
5 tháng 11 2021
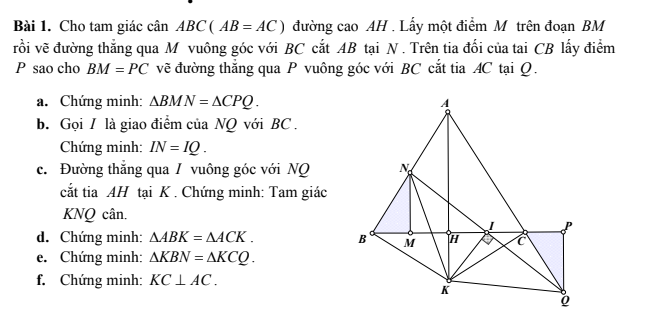
a, Vì tam giác ABC cân tại A nên \(\widehat{NBM}=\widehat{ACB}\)
Mà \(\widehat{ACB}=\widehat{PCQ}\left(đối.đỉnh\right)\Rightarrow\widehat{NBM}=\widehat{PCQ}\)
Mà \(\widehat{NMB}=\widehat{CPQ}=90^0;BM=PC\)
Do đó \(\Delta BMN=\Delta CPQ\left(g.c.g\right)\)
b, Vì \(BM//PQ\left(\perp BP\right)\) nên \(\widehat{MNI}=\widehat{IQP}\)
Mà \(\widehat{NMI}=\widehat{IPQ}=90^0;MN=PQ\left(\Delta BMN=\Delta CPQ\right)\)
Do đó \(\Delta IMN=\Delta IPQ\left(g.c.g\right)\)
\(\Rightarrow IN=IQ\)
c, Vì IK là đường cao cũng là trung tuyến tam giác KNQ nên tam giác KNQ cân tại K
9 tháng 12 2019
Ta có: \(x^2\ge0;\left|x+y\right|\ge0;\forall x,y\)
=> \(M=2015+3\left(x^2+1\right)^{2016}+\left|x+y\right|^{2017}\)
\(\ge2015+3\left(0+1\right)^{2016}+0^{2017}=2018\)
Dấu "=" xảy ra khi và chỉ khi: \(\hept{\begin{cases}x^2=0\\\left|x+y\right|=0\end{cases}\Leftrightarrow x=y=0}\)
Vậy gtnn của M = 2018 đạt tại x = y = 0.
6 tháng 3 2020
Đặt \(\frac{x}{a}=\frac{y}{b}=\frac{z}{c}=k\)
\(=>\hept{\begin{cases}x=ak\\y=bk\\z=ck\end{cases}}\)
Thay vào ta có :
\(\frac{bx-cy}{a}=\frac{cx-az}{b}=\frac{ay-bx}{c}\)
\(< =>\frac{bak-cbk}{a}=\frac{cak-ack}{b}=\frac{abk-bak}{c}\)
\(< =>\frac{a-c}{a}=0=0\)
Vậy ta cm đc khi c=a
HN
1
31 tháng 10 2015
Ta có:
\(2^{2014}-2^{2012}=2^{2012}.\left(4-1\right)=2^{2011}.2.3=2^{2011}.6\) chia hết cho 6
NT
1
9 tháng 7 2016
/ x + 2 / > 7
Th1 : \(x+2\ge0=>x\ge-2\)
PT trở thành :
\(x+2>7\)
\(=>x>5\)
TH2 : \(x+2< 0=>x< -2\)
Pt trở thành :
\(-x-2>7\)
\(=>-x=9=>x>-9\)
b) Th1 : \(x-1\ge0=>x\ge1\)
Ta có : \(x-1< 3=>x< 4\)
Th2 : \(x-1< 0=>x< 1\)
Ta có : \(-x+1< 3=>-x< 2=>x< -2\)