
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a/ \(\left(x-3\right)^2+6\left(x-3\right)+9\)
\(=\left(x-3\right)^2+2.\left(x-3\right).3+3^2\)
\(=\left(x-3+3\right)^2=x^2\)
==========
b/ \(\left(x+2021\right)^2+2\left(x+2021\right)\left(x-2021\right)+\left(x-2021\right)^2\)
\(=\left(x+2021+x-2021\right)^2=4x^2\)
===========
c/ \(2022^2-2.2021.2022+2021^2\)
\(=\left(2022-2021\right)^2=1\)
==========
d/ \(\left(x+44\right)^2-88\left(x+44\right)+1936\)
\(=\left(x+44\right)^2-2.\left(x+44\right).44+44^2\)
\(=\left(x+44-44\right)^2=x^2\)
d: Ta có: \(\left(x+44\right)^2-88\left(x+44\right)+1936\)
\(=\left(x+44-44\right)^2\)
\(=x^2\)

Bài 6:
a: Xét tứ giác AECH có
M là trung điểm của AC
M là trung điểm của HE
Do đó: AECH là hình bình hành
mà \(\widehat{AHC}=90^0\)
nên AECH là hình chữ nhật


a: BC=căn 6^2+8^2=10cm
bD là phân giác
=>AD/AB=CD/BC
=>AD/3=CD/5=(AD+CD)/(3+5)=8/8=1
=>AD=3cm; CD=5cm
b: Xét ΔBHA vuông tại H và ΔBAC vuông tại A có
góc B chung
=>ΔBHA đồng dạng với ΔBAC
=>BH/BA=BA/BC
=>BH*BC=BA^2
c: Xét ΔBHA có BI là phân giác
nên IH/IA=BH/BA
=>IH/IA=BA/BC=AD/DC

\(2b,=\left(2x^3-4x^2-4x^2+8x-2x+4-9\right):\left(2x-4\right)\\ =\left[\left(2x-4\right)\left(x^2-2x-2\right)-9\right]:\left(2x-4\right)\\ =x^2-2x-2\left(\text{ dư -9}\right)\)



a: Xét ΔADH vuông tại H và ΔBCI vuông tại I có
AD=BC
\(\widehat{D}=\widehat{C}\)
Do đó: ΔADH=ΔBCI
Suy ra: DH=CI


 đây bạn😀
đây bạn😀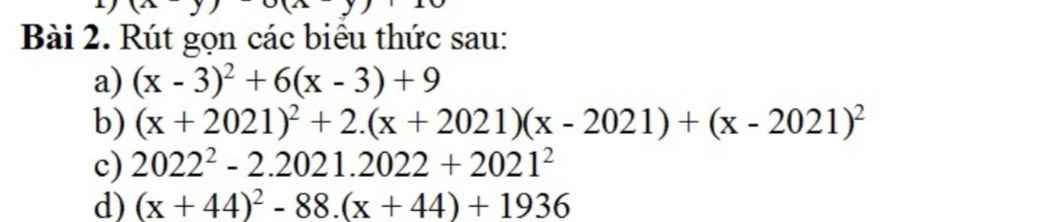



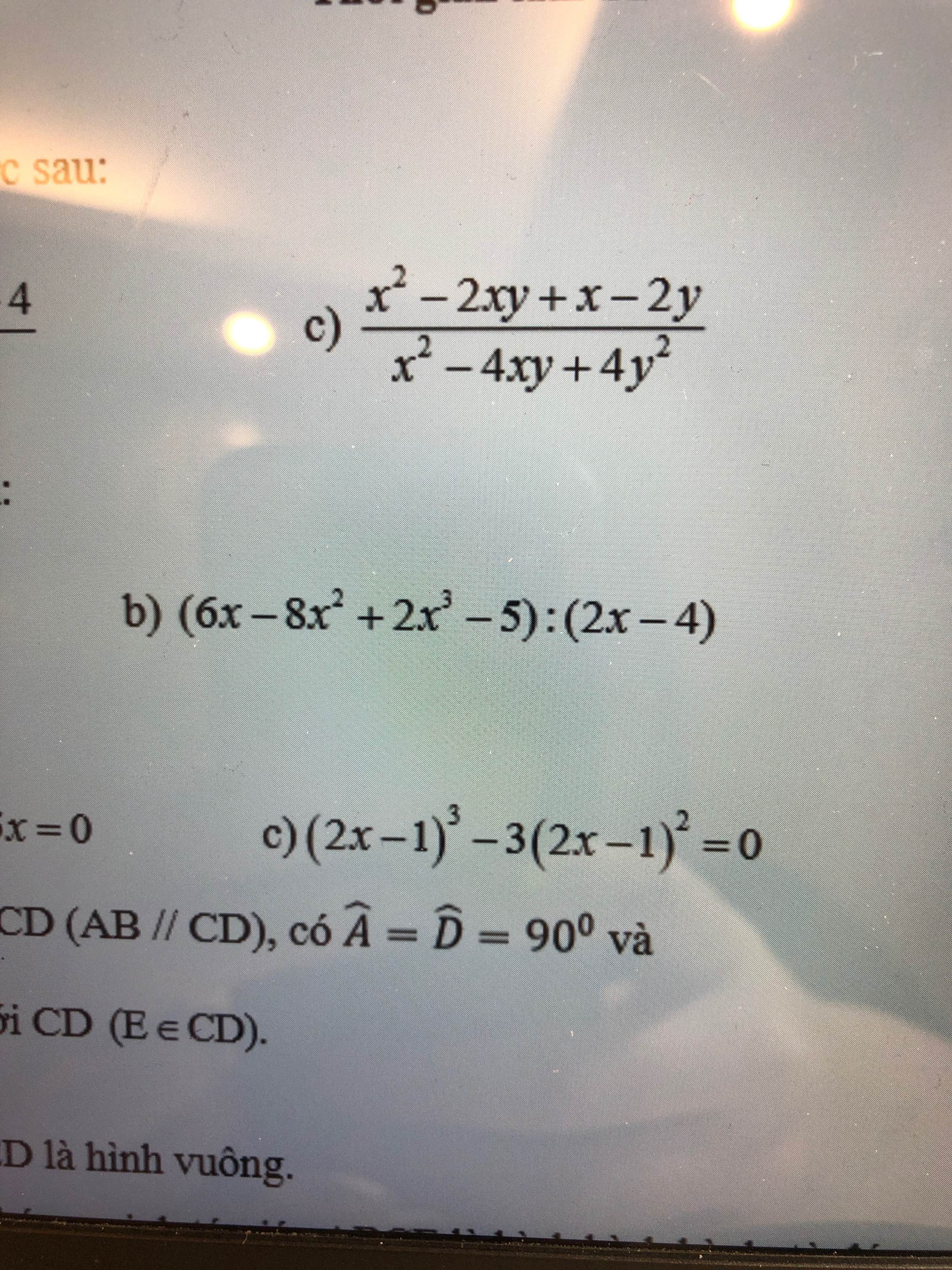


 Giúp mình với mn ơi:(
Giúp mình với mn ơi:(