Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a. Chu vi là \(\left(12+5\right).2=34\left(m\right)\)
Diện tích là \(12.5=60\left(m^2\right)=600000\left(cm^2\right)\)
b. Cần lát \(600000:\left(40.40\right)=375\) viên gạch

\(\Leftrightarrow164-4\left(x-5\right)=80\\ \Leftrightarrow4\left(x-5\right)=84\\ \Leftrightarrow x-5=21\Leftrightarrow x=26\)



\(B=2+2^2+2^3+2^4+...+2^{99}+2^{100}=2\left(1+2^2+2^3+2^4\right)+...+2^{96}\left(1+2^2+2^3+2^4\right)=2.31+2^6.31+...+2^{96}.31=31\left(2+2^6+...+2^{96}\right)⋮31\)

c: Trường hợp 1: n=2k
\(\Leftrightarrow n\left(n+2017\right)=2k\left(2k+2017\right)⋮2\)
Trường hợp 2: n=2k+1
\(\Leftrightarrow n\left(n+2017\right)=\left(2k+1\right)\left(2k+2018\right)⋮2\)

\(A=7\left(1+7+7^2\right)+...+7^{118}\left(1+7+7^2\right)\)
\(=57\left(1+...+7^{118}\right)⋮57\)

2S = 2 + 2^2 + 2^3 + ...+ 2^64
2S + 1 = 1 + 2 + 2^2 + ... + 2^64
2S - S = 2^64 - 1
Vậy S = 2^64 - 1
\(A=2^2+2^3+...+2^{62}+2^{63}\)
\(2A=2^3+2^4+...+2^{63}+2^{64}\)
\(2A-A=\left(2^3+2^4+...+2^{63}+2^{64}\right)-\left(2^2+2^3+...+2^{62}+2^{63}\right)\)
\(A=2^{64}-2^2\)


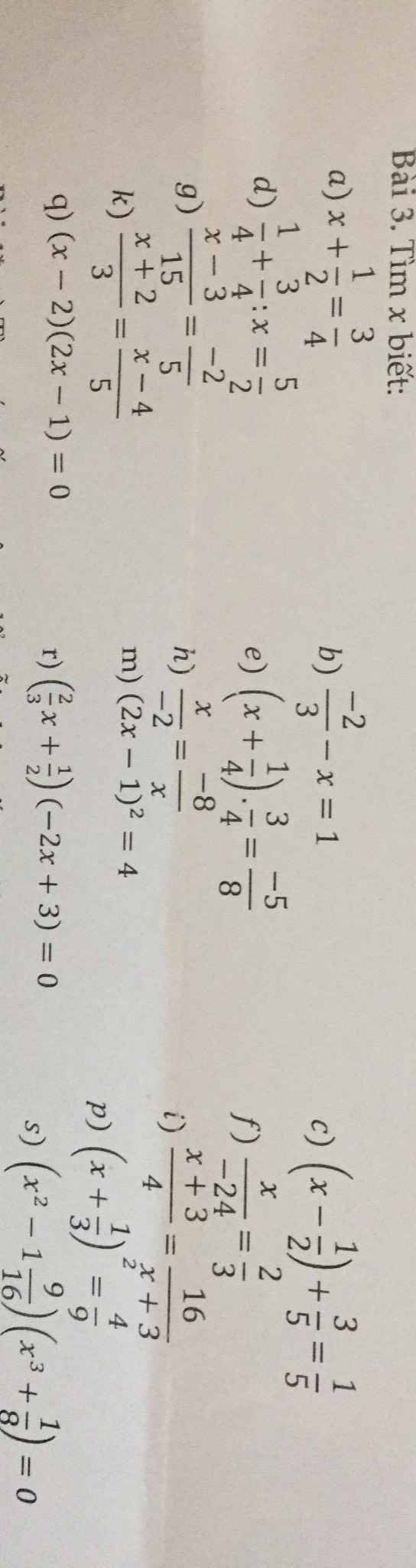
 help me, pls. Sắp đến giờ nộp bài rồi, các bn giúp mình với
help me, pls. Sắp đến giờ nộp bài rồi, các bn giúp mình với
3x x 2 + 15 = 33
<=> 3x = 9
<=> x = 2
3x . 2 + 15 = 33
3x . 2 = 33 - 15 = 18
3x = 18 : 2 = 9 = 32
=> x = 2