
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 2:
\(\dfrac{12}{-24}=\dfrac{12:12}{-24:12}=\dfrac{1}{-2}\)
\(\dfrac{-39}{75}=\dfrac{-39:3}{75:3}=\dfrac{-13}{25}\)
\(\dfrac{132}{-264}=\dfrac{132:132}{-264:132}=\dfrac{1}{-2}\)
Bài 3:
\(\dfrac{1}{-2}=\dfrac{-1}{2};\dfrac{-3}{-5}=\dfrac{3}{5};\dfrac{2}{-7}=\dfrac{-2}{7}\)
Bài 4:
\(15p=\dfrac{1}{4}h;20p=\dfrac{1}{3}h;45p=\dfrac{3}{4}h;50p=\dfrac{5}{6}h\)

Bài 4:
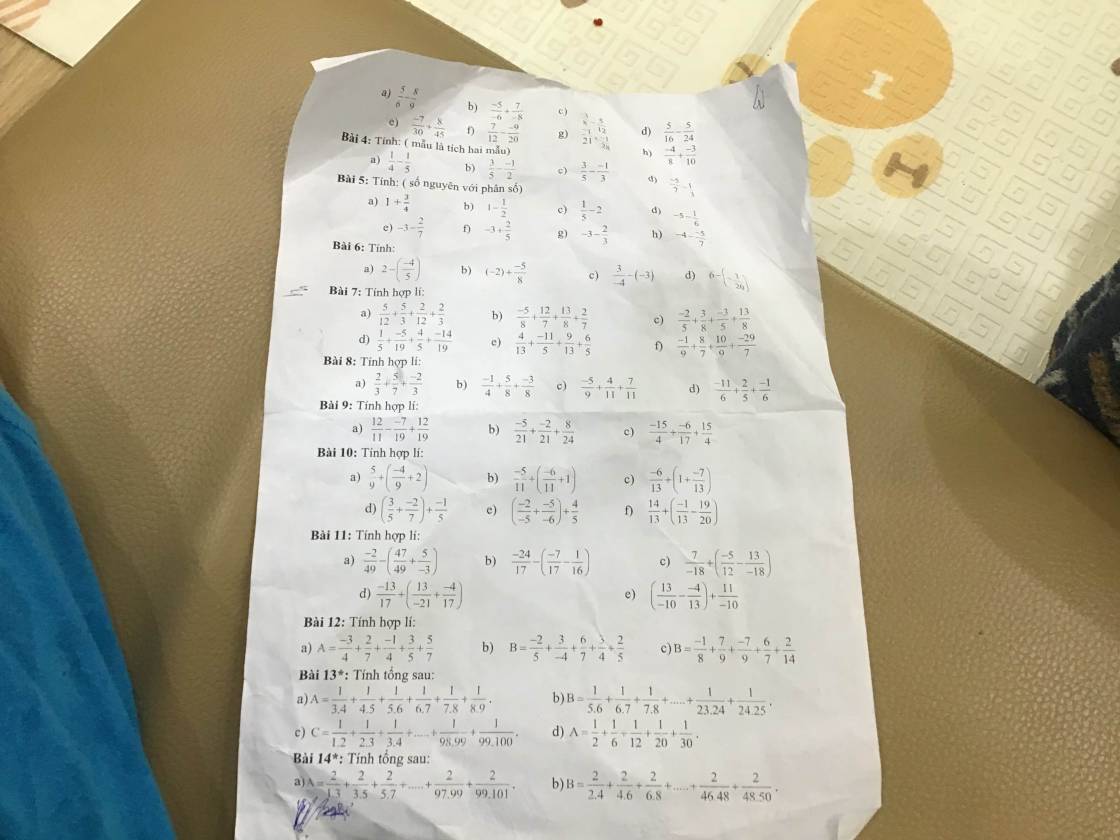
a; \(\dfrac{1}{4}\) - \(\dfrac{1}{5}\) = \(\dfrac{5}{20}\) - \(\dfrac{4}{20}\) = \(\dfrac{1}{20}\)
b; \(\dfrac{3}{5}\) - \(\dfrac{-1}{2}\) = \(\dfrac{6}{10}\) + \(\dfrac{5}{10}\) = \(\dfrac{11}{10}\)
c; \(\dfrac{3}{5}\) - \(\dfrac{-1}{3}\) = \(\dfrac{9}{15}\) + \(\dfrac{5}{15}\) = \(\dfrac{14}{15}\)
d; \(\dfrac{-5}{7}\) - \(\dfrac{1}{3}\)= \(\dfrac{-15}{21}\) - \(\dfrac{7}{21}\)= \(\dfrac{-22}{21}\)
Bài 5
a; 1 + \(\dfrac{3}{4}\) = \(\dfrac{4}{4}\) + \(\dfrac{3}{4}\) = \(\dfrac{7}{4}\) b; 1 - \(\dfrac{1}{2}\) = \(\dfrac{2}{2}\) - \(\dfrac{1}{2}\) = \(\dfrac{1}{2}\)
c; \(\dfrac{1}{5}\) - 2 = \(\dfrac{1}{5}\) - \(\dfrac{10}{5}\) = \(\dfrac{-9}{5}\) d; -5 - \(\dfrac{1}{6}\) = \(\dfrac{-30}{6}\) - \(\dfrac{1}{6}\) = \(\dfrac{-31}{6}\)
e; - 3 - \(\dfrac{2}{7}\)= \(\dfrac{-21}{7}\) - \(\dfrac{2}{7}\)= \(\dfrac{-23}{7}\) f; - 3 + \(\dfrac{2}{5}\) = \(\dfrac{-15}{5}\) + \(\dfrac{2}{5}\)= - \(\dfrac{13}{5}\)
g; - 3 - \(\dfrac{2}{3}\) = \(\dfrac{-9}{3}\) - \(\dfrac{2}{3}\) = \(\dfrac{-11}{3}\) h; - 4 - \(\dfrac{-5}{7}\) = \(\dfrac{-28}{7}\)+ \(\dfrac{5}{7}\) = - \(\dfrac{23}{7}\)

Bài 5:
a. Gọi $d=ƯCLN(n-2, n+1)$
$\Rightarrow n-2\vdots d; n+1\vdots d$
$\Rightarrow (n+1)-(n-2)\vdots d$
$\Rightarrow 3\vdots d\Rightarrow d\in \left\{1; 3\right\}$
Để ps tối giản thì $n-2\not\vdots 3$
$\Leftrightarrow n\neq 3k+2$ với $k$ là số tự nhiên bất kỳ.
b.
Gọi $d=ƯCLN(n+5, n-2)$
$\Rightarrow n+5\vdots d; n-2\vdots d$
$\Rightarrow (n+5)-(n-2)\vdots d$
$\Rightarrow 7\vdots d$
$\Rightarrow d\in \left\{1; 7\right\}$
Để ps tối giản thì $n-2\not\vdots 7$
$\Rightarrow n\neq 7k+2$ với $k$ là số tự nhiên bất kỳ.

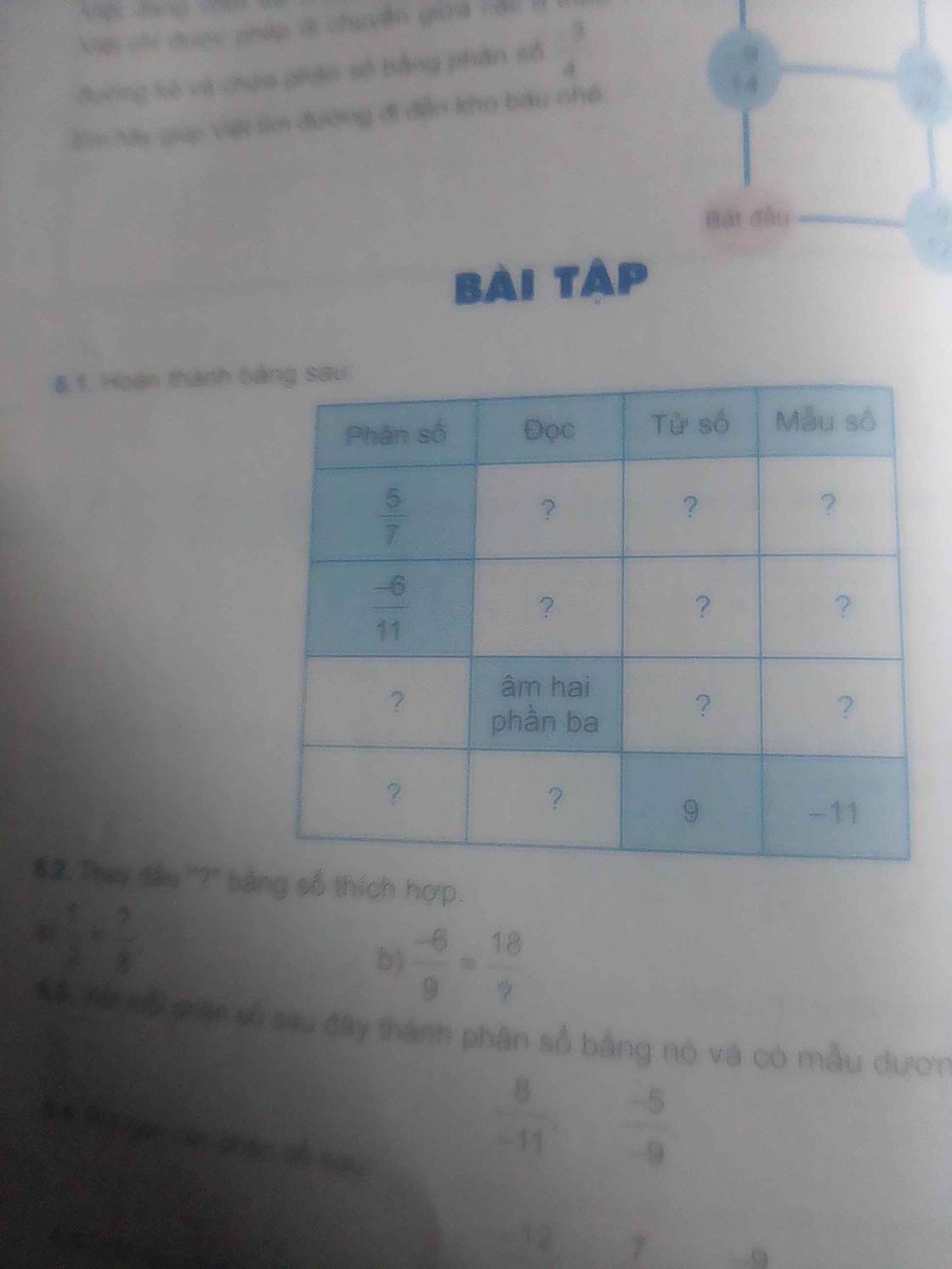
| Phân số | Đọc | Tử Số | Mẫu số |
| \(\dfrac{5}{7}\) | Năm phần bẩy | 5 | 7 |
| \(\dfrac{-6}{11}\) | âm sáu phần mười một | -6 | 11 |
| \(\dfrac{-2}{13}\) | âm hai phần ba | -2 | 13 |
| \(\dfrac{9}{-11}\) | chín phần âm mười một | 9 | -11 |


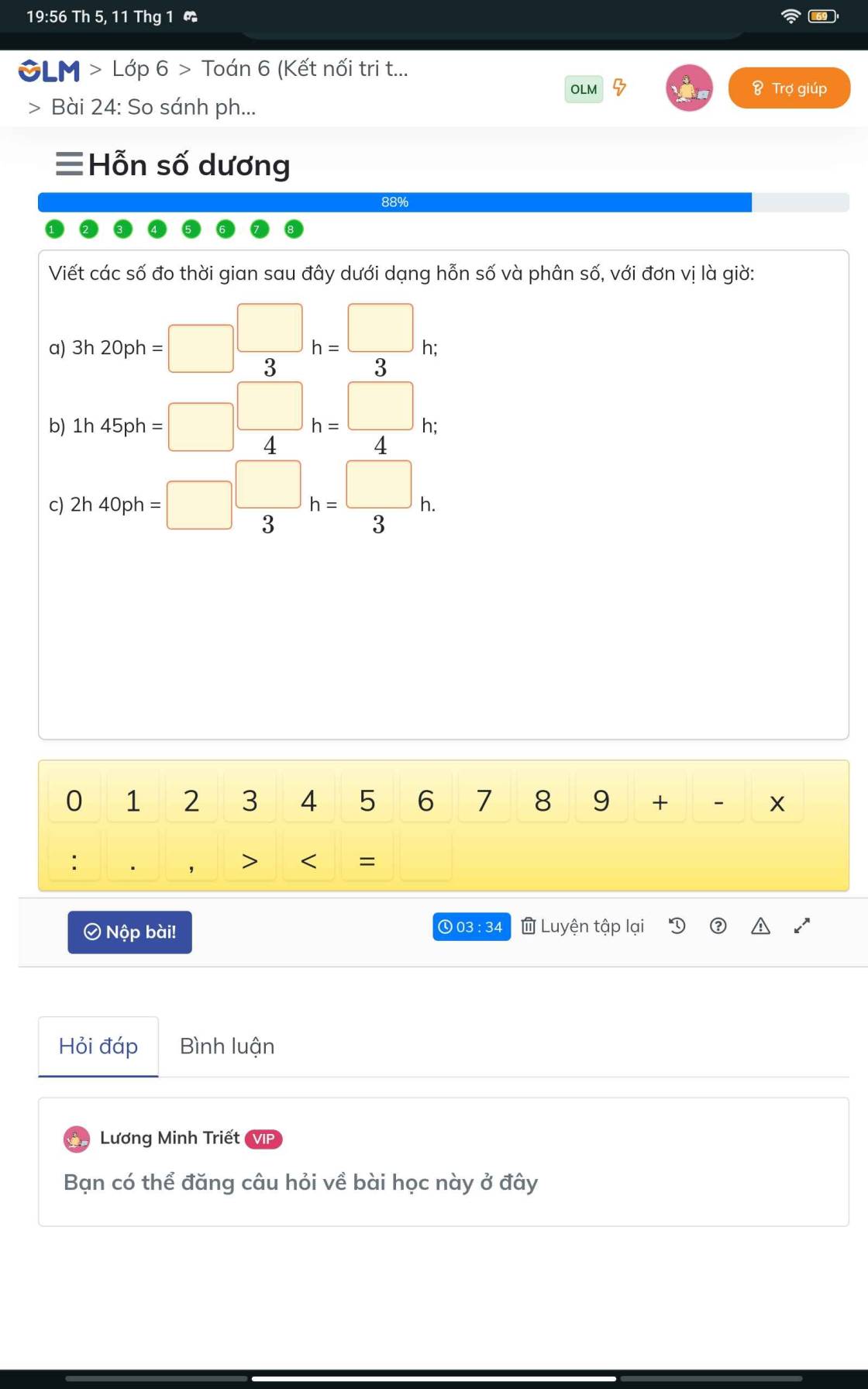
a) 3h 20ph = 3 và 1/3 = 10/3
b) 1h 45 ph = 1 và 3/4 = 7/4
c) 2h 40 ph = 2 và 2/3 = 8/3

\(a,-\dfrac{9}{4}< 0;\dfrac{1}{3}>0.Nên:-\dfrac{9}{4}< \dfrac{1}{3}\\ b,-\dfrac{8}{3}< -2;\dfrac{4}{-7}>-1.Nên:-\dfrac{8}{3}< -2< -1< \dfrac{4}{-7}\\ Vậy:-\dfrac{8}{3}< \dfrac{4}{-7}\\ c,\dfrac{9}{-5}< -1;\dfrac{7}{-10}>-1.Nên:\dfrac{9}{-5}< -1< \dfrac{7}{-10}.Vậy:\dfrac{9}{-5}< \dfrac{7}{-10}\\ d,\dfrac{3}{14}>0;-\dfrac{6}{14}< 0.Nên:\dfrac{3}{14}>0>-\dfrac{6}{14}.Vậy:\dfrac{3}{14}>-\dfrac{6}{14}\\ e,\dfrac{7}{-12}=\dfrac{7.3}{-12.3}=\dfrac{21}{-36};\dfrac{11}{-18}=\dfrac{11.2}{-18.2}=\dfrac{22}{-36}\\ Vì:\dfrac{21}{-36}>\dfrac{22}{-36}.Nên:\dfrac{7}{-12}>\dfrac{11}{-18}\)
\(f,-\dfrac{4}{7}< -\dfrac{1}{2};-\dfrac{4}{10}>\dfrac{-1}{2}.Nên:-\dfrac{4}{7}< -\dfrac{1}{2}< -\dfrac{4}{10}.Vậy:-\dfrac{4}{7}< -\dfrac{4}{10}\\ g,-\dfrac{8}{15}< -\dfrac{1}{2};\dfrac{5}{-24}>-\dfrac{1}{2}.Nên:-\dfrac{8}{15}< -\dfrac{1}{2}< \dfrac{5}{-24}.Vậy:-\dfrac{8}{15}< \dfrac{5}{-24}\\ h,\dfrac{69}{-230}=\dfrac{69:23}{-230:23}=\dfrac{3}{-10};\dfrac{-39}{143}=\dfrac{-39:13}{143:13}=\dfrac{-3}{11}\\ Vì:\dfrac{-3}{10}< -\dfrac{3}{11}.Vậy:\dfrac{69}{-230}< \dfrac{-39}{143}\\ i,\dfrac{7}{41}=1-\dfrac{34}{41};\dfrac{13}{47}=1-\dfrac{34}{47}\\ Vì:\dfrac{34}{41}>\dfrac{34}{47}.Nên:1-\dfrac{34}{41}< 1-\dfrac{34}{47}.Vậy:\dfrac{7}{41}< \dfrac{13}{47}\)






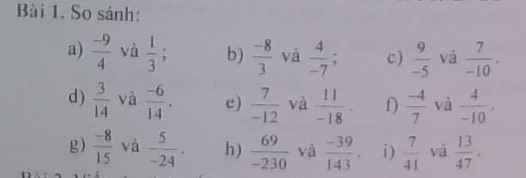
Bài 22:
a. Sai. Hình thoi có 4 cạnh bằng nhau
b. Sai.Hình bình hành có hai đường chéo cắt nhau tại trung điểm mỗi đường.
c. Đúng
d. Đúng
e. Sai. Không phải hình nào cũng có trục đối xứng.
f. Đúng
g. Đúng
i. Sai. Hình chữ nhật có hai đường chéo bằng nhau
k. Sai. Hình lục giác có 3 đường chéo chính.
l. Sai. Hình lúc giác đều có 6 cạnh bằng nhau, 6 góc ở đỉnh bằng nhau.
Bài 23:
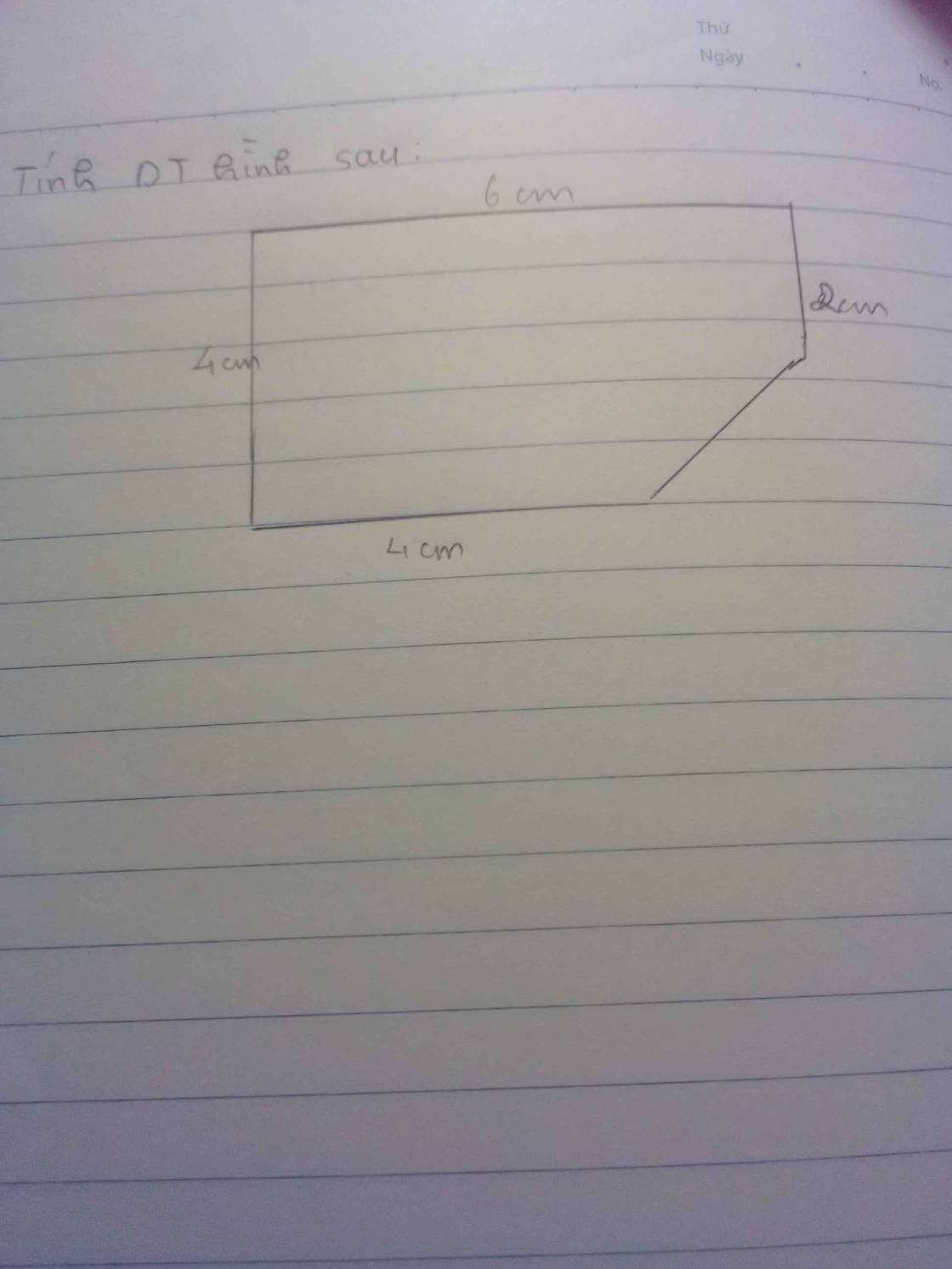
a. Khi chiều rộng bằng chiều dài, thì mảnh đất trở thành hình vuông có độ dài cạnh 10 m
Diện tích mảnh đất trồng lạc: $10\times 10=100$ (m2)
b. Chiều dài của bờ rào là:
$2\times (10+10)=40$ (m)