K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DX
0
DX
0
22 tháng 1
Bài 2:
Gọi độ dài quãng đường AB là x(km)
(Điều kiện: x>0)
Thời gian đi từ A đến B là \(\dfrac{x}{25}\left(giờ\right)\)
Thời gian đi từ B về A là \(\dfrac{x}{30}\left(giờ\right)\)
Tổng thời gian cả đi lẫn về là \(3h40p=\dfrac{11}{3}\left(giờ\right)\) nên ta có phương trình:
\(\dfrac{x}{25}+\dfrac{x}{30}=\dfrac{11}{3}\)
=>\(\dfrac{6x+5x}{150}=\dfrac{11}{3}\)
=>\(\dfrac{11x}{150}=\dfrac{11}{3}\)
=>\(x=\dfrac{11}{3}:\dfrac{11}{150}=50\left(nhận\right)\)
Vậy: ĐỘ dài quãng đường AB là 50km
Bài 3:
1:
a: Sửa đề: ΔABC vuông tại A
Xét ΔCHA vuông tại H và ΔCAB vuông tại A có
\(\widehat{ACB}\) chung
Do đó: ΔCHA~ΔCAB
b: Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=3^2+4^2=25\)
=>\(BC=\sqrt{25}=5\left(cm\right)\)
Xét ΔCAB có CD là phân giác
nên \(\dfrac{AD}{AC}=\dfrac{DB}{BC}\)
=>\(\dfrac{AD}{4}=\dfrac{DB}{5}\)
mà AD+DB=AB=3cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AD}{4}=\dfrac{DB}{5}=\dfrac{AD+DB}{4+5}=\dfrac{3}{9}=\dfrac{1}{3}\)
=>\(AD=4\cdot\dfrac{1}{3}=\dfrac{4}{3}\left(cm\right);DB=5\cdot\dfrac{1}{3}=\dfrac{5}{3}\left(cm\right)\)
c: Xét ΔCAH có CI là phân giác
nên \(\dfrac{IH}{AI}=\dfrac{CH}{CA}\left(1\right)\)
Xét ΔCAB có CD là phân giác
nên \(\dfrac{AC}{BC}=\dfrac{AD}{DB}\left(2\right)\)
Ta có: ΔCHA~ΔCAB
=>\(\dfrac{CH}{CA}=\dfrac{CA}{CB}\left(3\right)\)
Từ (1),(2),(3) suy ra \(\dfrac{CA}{CB}=\dfrac{IH}{IA}\)
VT
2
28 tháng 6 2023
b: AD là phân giác
=>DB/AB=DC/AC
=>DB/DC=AB/AC=3/4
=>DB/3=DC/4
mà DB+DC=BC=14
nên DB/3=DC/4=14/7=2
=>DB=6cm; DC=8cm
19 tháng 4 2018
câu vừa nãy mình làm sai nha
nếu x = 1 thì phép tính đó âm mất rùi
nên là bài này không có kết quả
19 tháng 4 2018
Vì x^4= x.x.x.x
4x+3=x.4+3
=>x^4>4x+3
=>x^4-4x+3>0
=>x^4-4x+3 không âm với mọi x
22 tháng 12 2021
a: Thay x=-4 vào B, ta được:
\(B=\dfrac{1-2\cdot\left(-4\right)}{2-\left(-4\right)}=\dfrac{1+8}{2+4}=\dfrac{9}{6}=\dfrac{3}{2}\)
25 tháng 12 2021
a: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
Do đó: AEHF là hình chữ nhật
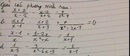
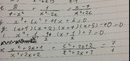
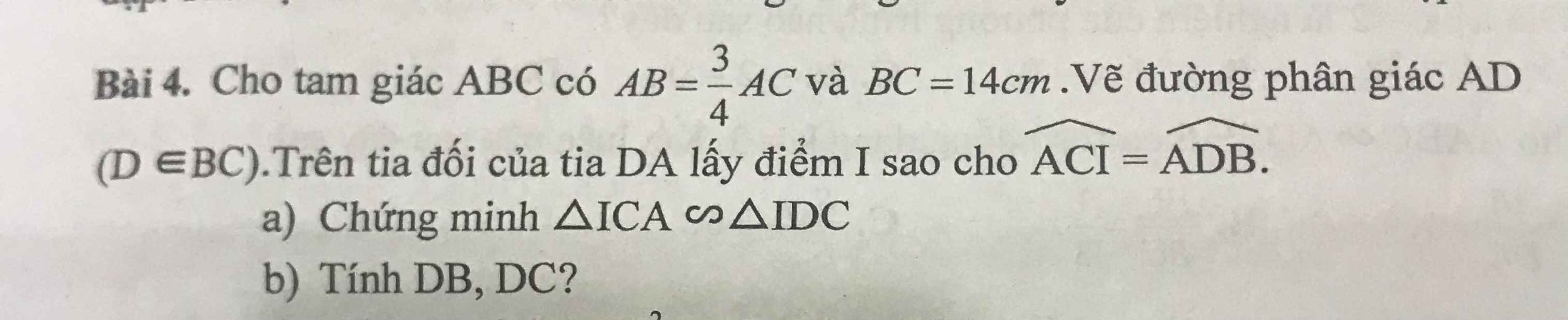
mình làm mẫu 1 câu nhé !
\(\frac{x+2}{x-2}-\frac{x-2}{x+2}=\frac{4}{x^2-4}\)ĐK : \(x\ne\pm2\)
\(\Leftrightarrow\frac{\left(x+2\right)^2}{\left(x-2\right)\left(x+2\right)}-\frac{\left(x-2\right)^2}{\left(x-2\right)\left(x+2\right)}=\frac{4}{\left(x-2\right)\left(x+2\right)}\)
Khử mẫu : \(x^2+2x+1-x^2+2x-1=4\)
\(\Leftrightarrow4x=4\Leftrightarrow x=1\)( tmđk )
Vậy tập nghiệm của phương trình là S = { 1 }
e, \(\frac{2}{4-x^2}+\frac{1}{x^2-2x}=\frac{x-4}{x^2+2x}\)ĐK : \(x\ne0;\pm2\)
\(\Leftrightarrow\frac{2}{\left(2-x\right)\left(x+2\right)}+\frac{1}{x\left(x-2\right)}-\frac{x-4}{x\left(x+2\right)}=0\)
\(\Leftrightarrow\frac{2x}{x\left(2-x\right)\left(x+2\right)}-\frac{x+2}{x\left(2-x\right)\left(x+2\right)}-\frac{\left(x-4\right)\left(x-2\right)}{x\left(x-2\right)\left(x+2\right)}=0\)
Khử mẫu : \(2x-x-2-\left(x^2-2x-4x+4\right)=0\)
\(\Leftrightarrow x-2-x^2+6x-4=0\)
\(\Leftrightarrow-x^2+7x-6=0\Leftrightarrow-\left(x-6\right)\left(x-1\right)=0\Leftrightarrow x=6;1\)
Vậy tập nghiệm của phương trình là S = { 1 ; 6 }