GIÚP MÌNH VỚI. GẤP LẮM RỒI
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
1
26 tháng 2 2022
a, \(2y^2\left(8y^6\right)y=16y^9\)
b, \(=\dfrac{3}{4}x^3y^4\)
c, \(=10x^3y^4z^8\)
d, \(=\left(\dfrac{3}{4}x^2y^3\right)\left(\dfrac{12}{5}x^4\right)=\dfrac{9}{5}x^6y^3\)
e, \(=-\dfrac{5}{4}x^5y^{10}\)
f, \(=120x^4y^6z^4\)
4 tháng 12 2021
a: Xét ΔABH vuông tại H và ΔMBH vuông tại H có
HB chung
HA=HM
Do đó: ΔABH=ΔMBH
2D
Mn giải giúp mình với mình cần gấp lắm hôm nay mình pgair nộp rồi
3
14 tháng 10 2021
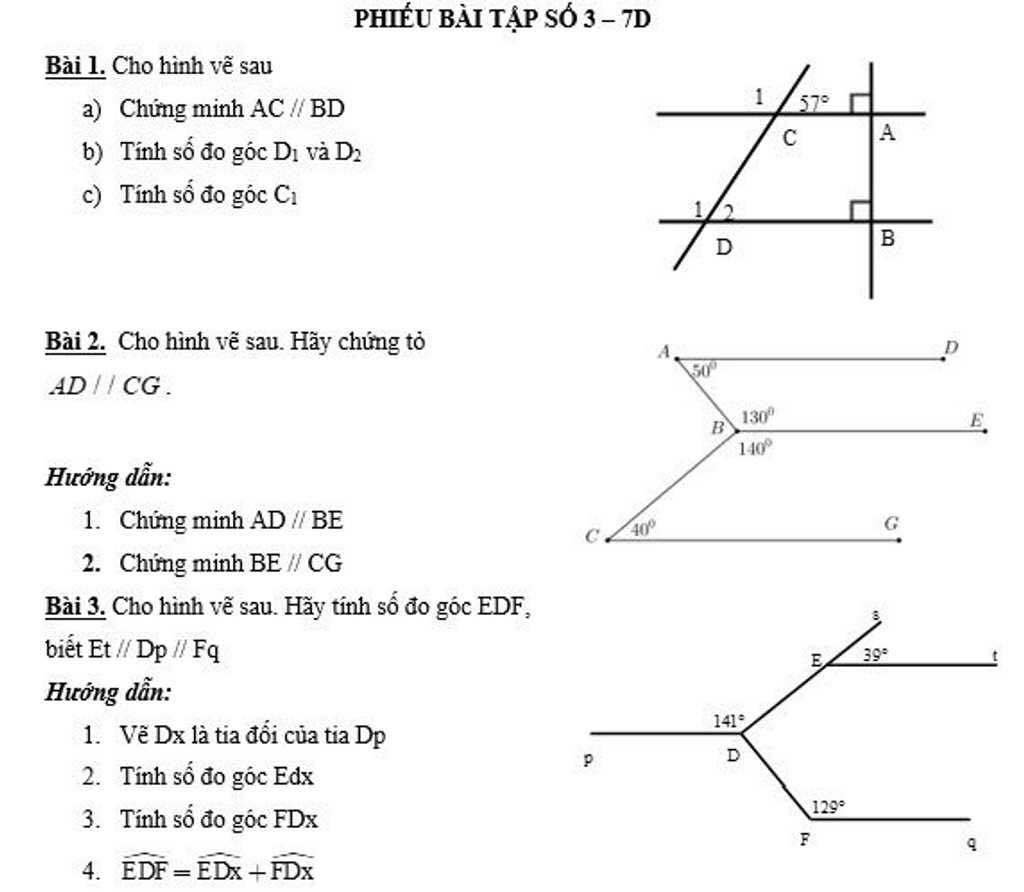
\(1,\\ a,\left\{{}\begin{matrix}AC\perp AB\\BD\perp AB\end{matrix}\right.\Rightarrow AC//BD\\ b,AC//BD\Rightarrow\widehat{D_2}=\widehat{C_1}=57^0\left(đồng.vị\right)\\ \widehat{D_2}+\widehat{D_1}=180^0\left(kề.bù\right)\Rightarrow\widehat{D_1}=180^0-57^0=123^0\\ c,AC//BD\Rightarrow\widehat{D_1}=\widehat{C_1}=123^0\left(đồng.vị\right)\)
14 tháng 10 2021
\(2,\\ \widehat{DAB}+\widehat{ABE}=50^0+130^0=180^0\)
Mà 2 góc này ở vị trí TCP nên AD//BE (1)
\(\widehat{EBC}+\widehat{BCG}=140^0+40^0=180^0\)
Mà 2 góc này ở vị trí TCP nên BE//CG (2)
Từ (1)(2) ta được AD//CG
IC
1
5 tháng 11 2021
a, Vì tam giác ABC cân tại A nên \(\widehat{NBM}=\widehat{ACB}\)
Mà \(\widehat{ACB}=\widehat{PCQ}\left(đối.đỉnh\right)\Rightarrow\widehat{NBM}=\widehat{PCQ}\)
Mà \(\widehat{NMB}=\widehat{CPQ}=90^0;BM=PC\)
Do đó \(\Delta BMN=\Delta CPQ\left(g.c.g\right)\)
b, Vì \(BM//PQ\left(\perp BP\right)\) nên \(\widehat{MNI}=\widehat{IQP}\)
Mà \(\widehat{NMI}=\widehat{IPQ}=90^0;MN=PQ\left(\Delta BMN=\Delta CPQ\right)\)
Do đó \(\Delta IMN=\Delta IPQ\left(g.c.g\right)\)
\(\Rightarrow IN=IQ\)
c, Vì IK là đường cao cũng là trung tuyến tam giác KNQ nên tam giác KNQ cân tại K
N
0
N
0
25 tháng 7 2021
a) Xét ΔNMD và ΔNED có
NM=NE(gt)
\(\widehat{MND}=\widehat{END}\)(ND là tia phân giác của \(\widehat{NME}\))
ND chung
Do đó: ΔNMD=ΔNED(c-g-c)
Suy ra: \(\widehat{NMD}=\widehat{NED}\)(hai góc tương ứng)
mà \(\widehat{NMD}=90^0\)(gt)
nên \(\widehat{NED}=90^0\)
hay DE\(\perp\)NP
b) Ta có: NM=NE(gt)
nên N nằm trên đường trung trực của ME(1)
Ta có: DM=DE(ΔNMD=ΔNED)
nên D nằm trên đường trung trực của ME(2)
Từ (1) và (2) suy ra ND là đường trung trực của ME
18 tháng 9 2021
a) \(\left(3x^2+5x-3\right)+\left(x-3x^2-3\right)=0\)
\(\Leftrightarrow6x-6=0\)
\(\Leftrightarrow6x=6\Leftrightarrow x=1\)
b) \(\left(3x^2-5x\right)-\left(3x^2+x-12\right)=0\)
\(\Leftrightarrow3x^2-5x-3x^2-x+12=0\)
\(\Leftrightarrow-6x=-12\Leftrightarrow x=2\)
N
0