
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bạn ơi, làm như vậy thì quá ngắn rồi ạ, với lại bạn làm thiếu mất đề bài của mình rồi

Bài 1:
a: Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=3.6\left(cm\right)\\CH=6.4\left(cm\right)\end{matrix}\right.\)
b: Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HF là đường cao ứng với cạnh huyền AB, ta được:
\(AF\cdot AB=AH^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HE là đường cao ứng với cạnh huyền AC, ta được:
\(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AF\cdot AB=AE\cdot AC\)

Lời giải:
Đặt \(\sqrt[3]{5\sqrt{2}+7}=m; \sqrt[3]{5\sqrt{2}-7}=n\)
\(m^3-n^3=14\)
\(mn=1\)
\((a+b+c)^3=(m-n)^3=m^3-3mn(m-n)-n^3=14-3(m-n)\)
\(\Leftrightarrow (a+b+c)^3=14-3(a+b+c)\)
\(\Leftrightarrow (a+b+c)^3+3(a+b+c)-14=0\)
\(\Leftrightarrow (a+b+c)^2[(a+b+c)-2]+2(a+b+c)(a+b+c-2)+7(a+b+c-2)=0\)
\(\Leftrightarrow (a+b+c-2)[(a+b+c)^2+2(a+b+c)+7]=0\)
Dễ thấy biểu thức trong ngoặc vuông $>0$ nên $a+b+c-2=0$
$\Leftrightarrow a+b+c=2$
$ab+bc+ac=\frac{(a+b+c)^2-(a^2+b^2+c^2)}{2}=\frac{2^2-1}{2}=\frac{3}{2}$

a: Khi x<0 thì hàm số đồng biến
b: PTHĐGĐ là:
-x^2=2x-3
=>-x^2-2x+3=0
=>x^2+2x-3=0
=>(x+3)(x-1)=0
=>x=1 hoặc x=-3
=>y=-1 hoặc y=-9
c: Thay y=-4vào (P),ta được:
x^2=4
=>x=2 hoặc x=-2


a) \(\Leftrightarrow A=\dfrac{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}{\sqrt{x}\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}-\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(\Leftrightarrow A=\dfrac{x+2\sqrt{x}-3-x+2\sqrt{x}+3}{\sqrt{x}\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(\Leftrightarrow A=\dfrac{4\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}=\dfrac{4}{x-1}\)
b) \(A=7\) \(\Leftrightarrow\dfrac{4}{x-1}=7\)
\(\Leftrightarrow7x-7=4\) \(\Leftrightarrow7x=11\Leftrightarrow x=\dfrac{11}{7}\left(TM\right)\)
\(a,A=\dfrac{x+2\sqrt{x}-3-x+2\sqrt{x}+3}{\sqrt{x}\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}=\dfrac{4\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{4}{x-1}\\ b,A=7\Leftrightarrow x-1=\dfrac{4}{7}\Leftrightarrow x=\dfrac{11}{7}\left(tm\right)\)

Lời giải:
a. ĐKXĐ: $x>0; x\neq 4$
b.
\(M=\sqrt{x}.\left[\frac{1}{\sqrt{x}-2}+\frac{1}{\sqrt{x}+2}\right].\frac{x-4}{2\sqrt{x}}\)
\(=\frac{2\sqrt{x}}{(\sqrt{x}-2)(\sqrt{x}+2)}.\frac{x-4}{2}=\frac{2\sqrt{x}}{x-4}.\frac{x-4}{2}=\sqrt{x}\)
c. Để $M>3\Leftrightarrow \sqrt{x}>3\Leftrightarrow x>9$
Kết hợp đkxđ suy ra $x>9$ thì $M>3$




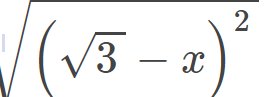
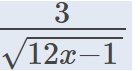 GIÚP MÌNH VỚI Ạ MÌNH CẦN GẤP Ạ
GIÚP MÌNH VỚI Ạ MÌNH CẦN GẤP Ạ




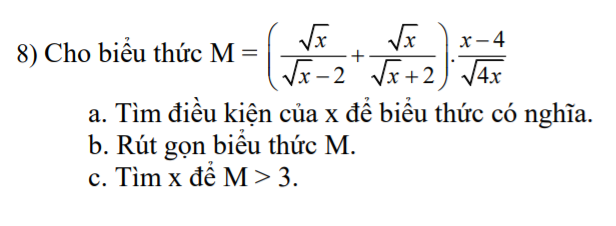

Điều kiện xác định : \(1\ge a\ge0\)
a, Ta có : \(\frac{\sqrt{1+a}}{\sqrt{1+a}-\sqrt{1-a}}+\frac{1-a}{\sqrt{1-a^2}-1+a}=\frac{\sqrt{1+a}+\sqrt{1-a}}{\sqrt{1+a}-\sqrt{1-a}}=\frac{1+\sqrt{1-a^2}}{a}\)
\(\sqrt{\frac{1}{a^2}-1}-\frac{1}{a}=\sqrt{\frac{1-a^2}{a^2}}-\frac{1}{a}=\frac{\sqrt{1-a^2}-1}{a}\)
\(\sqrt{a^2-2a+1}=\sqrt{\left(a-1\right)^2}=a-1\)
Suy ra \(Q=\frac{1+\sqrt{1-a^2}}{a}.\frac{\sqrt{1-a^2}-1}{a}.\left(a-1\right)=\frac{1-a^2-1}{a^2}.\left(a-1\right)=-1.\left(a-1\right)=1-a\)
b, Xét hiệu \(Q^3-Q=-2a+3a^2-a^3=-a\left(a^2-3a+2\right)=a\left(a-1\right)\left(2-a\right)\):vv
phải xét th a = 1 với a khác 1 nhé :)
gợi ý nè : a = 1 thì = nhau mà a khác 1 thì q^3 > q nhé
Tự làm 1 xíu nhé