
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
Đặt \(\sqrt[3]{5\sqrt{2}+7}=m; \sqrt[3]{5\sqrt{2}-7}=n\)
\(m^3-n^3=14\)
\(mn=1\)
\((a+b+c)^3=(m-n)^3=m^3-3mn(m-n)-n^3=14-3(m-n)\)
\(\Leftrightarrow (a+b+c)^3=14-3(a+b+c)\)
\(\Leftrightarrow (a+b+c)^3+3(a+b+c)-14=0\)
\(\Leftrightarrow (a+b+c)^2[(a+b+c)-2]+2(a+b+c)(a+b+c-2)+7(a+b+c-2)=0\)
\(\Leftrightarrow (a+b+c-2)[(a+b+c)^2+2(a+b+c)+7]=0\)
Dễ thấy biểu thức trong ngoặc vuông $>0$ nên $a+b+c-2=0$
$\Leftrightarrow a+b+c=2$
$ab+bc+ac=\frac{(a+b+c)^2-(a^2+b^2+c^2)}{2}=\frac{2^2-1}{2}=\frac{3}{2}$


Lời giải:
a. ĐKXĐ: $x>0; x\neq 4$
b.
\(M=\sqrt{x}.\left[\frac{1}{\sqrt{x}-2}+\frac{1}{\sqrt{x}+2}\right].\frac{x-4}{2\sqrt{x}}\)
\(=\frac{2\sqrt{x}}{(\sqrt{x}-2)(\sqrt{x}+2)}.\frac{x-4}{2}=\frac{2\sqrt{x}}{x-4}.\frac{x-4}{2}=\sqrt{x}\)
c. Để $M>3\Leftrightarrow \sqrt{x}>3\Leftrightarrow x>9$
Kết hợp đkxđ suy ra $x>9$ thì $M>3$


\(a,=2\sqrt{2}\left(\sqrt{5}-1\right)\sqrt{4+\sqrt{\left(\sqrt{5}-1\right)^2}}\\ =2\sqrt{2}\left(\sqrt{5}-1\right)\sqrt{4+\sqrt{5}-1}\\ =2\left(\sqrt{5}-1\right)\sqrt{6-2\sqrt{5}}\\ =2\left(\sqrt{5}-1\right)\sqrt{\left(\sqrt{5}-1\right)^2}\\ =2\left(\sqrt{5}-1\right)^2=2\left(6-2\sqrt{5}\right)=12-4\sqrt{5}\\ b,=\left(4+\sqrt{15}\right)\left(\sqrt{5}-\sqrt{3}\right)\sqrt{8-2\sqrt{15}}\\ =\left(4+\sqrt{15}\right)\left(\sqrt{5}-\sqrt{3}\right)\sqrt{\left(\sqrt{5}-\sqrt{3}\right)^2}\\ =\left(4+\sqrt{15}\right)\left(\sqrt{5}-\sqrt{3}\right)^2\\ =\left(4+\sqrt{15}\right)\left(8-2\sqrt{15}\right)\\ =32-8\sqrt{15}+8\sqrt{15}-30=2\)



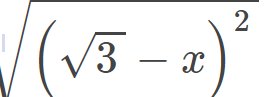
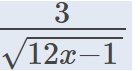 GIÚP MÌNH VỚI Ạ MÌNH CẦN GẤP Ạ
GIÚP MÌNH VỚI Ạ MÌNH CẦN GẤP Ạ
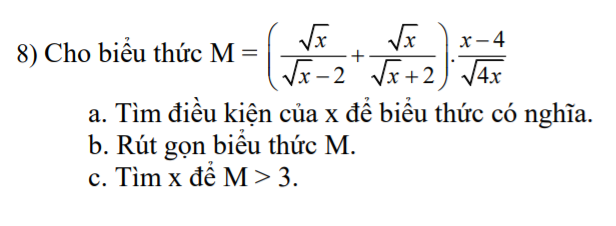








1.
ĐKXĐ: \(x\ge-\dfrac{1}{4}\)
\(\sqrt{x+2}+\sqrt{4x+1}=5\)
\(\Leftrightarrow\sqrt{x+2}-2+\sqrt{4x+1}-3=0\)
\(\Leftrightarrow\dfrac{x-2}{\sqrt{x+2}+2}+\dfrac{4\left(x-2\right)}{\sqrt{4x+1}+3}=0\)
\(\Leftrightarrow\left(x-2\right)\left(\dfrac{1}{\sqrt{x+2}+2}+\dfrac{4}{\sqrt{4x+1}+3}\right)=0\)
\(\Leftrightarrow x-2=0\) (do \(\dfrac{1}{\sqrt{x+2}+2}+\dfrac{4}{\sqrt{4x+1}+3}>0\))
\(\Leftrightarrow x=2\)
2.
\(\Leftrightarrow10x^2-5x-3-\sqrt{6x^2-3x+1}=0\)
\(\Leftrightarrow5\left(2x^2-x\right)-3-\sqrt{6x^2-3x+1}=0\)
Đặt \(\sqrt{6x^2-3x+1}=t>0\)
\(\Rightarrow6x^2-3x+1=t^2\Rightarrow3\left(2x^2-x\right)=t^2-1\)
\(\Rightarrow2x^2-x=\dfrac{t^2-1}{3}\)
Phương trình trở thành:
\(5.\dfrac{t^2-1}{3}-3-t=0\)
\(\Leftrightarrow5t^2-3t-14=0\Rightarrow\left[{}\begin{matrix}t=2\\t=-\dfrac{7}{5}\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow\sqrt{6x^2-3x+1}=2\)
\(\Leftrightarrow6x^2-3x+1=4\)
\(\Leftrightarrow2x^2-x-1=0\Rightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{1}{2}\end{matrix}\right.\)