
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a: \(VT=\left(\dfrac{\sqrt{7}\left(\sqrt{2}-1\right)}{2\left(\sqrt{2}-1\right)}+\dfrac{\sqrt{5}\left(\sqrt{3}-1\right)}{2\left(\sqrt{3}-1\right)}\right)\cdot\left(\sqrt{7}-\sqrt{5}\right)\)
\(=\left(\dfrac{\sqrt{7}+\sqrt{5}}{2}\right)\cdot\left(\sqrt{7}-\sqrt{5}\right)=\dfrac{7-5}{2}=\dfrac{2}{2}=1\)
=VP
b: \(VT=3-\sqrt{5}+2\left(\sqrt{5}+1\right)-\left|\sqrt{5}-2\right|\)
=3-căn 5+2căn 5+2-căn 5+2
=3+2+2=7
=VP

5:
a: =>2x+3=3+2căn 2
=>2x=2căn 2
=>x=căn 2
b: =>10+căn 3x=10+4căn 6
=>căn 3x=4căn 6=căn 96
=>3x=96
=>x=32
c: =>3x-2=7-4căn 3
=>3x=9-4căn 3
=>x=3-4/3*căn 3
a: =>\(2\cdot\sqrt{x-5}+\sqrt{x-5}-\sqrt{x-5}=4\)
=>2*căn x-5=4
=>căn x-5=2
=>x-5=4
=>x=9

Q = \(\dfrac{3\sqrt{x}}{x+1}\) (x \(\ge\) 0; x \(\ne\) 4)
Áp dụng BĐT Cô-si cho 2 số không âm x và 1 ta được:
\(\dfrac{x+1}{2}\ge\sqrt{x}\) (1)
\(\Leftrightarrow\) \(\dfrac{3\cdot\dfrac{x+1}{2}}{x+1}\ge\dfrac{3\sqrt{x}}{x+1}\) (x + 1 > 0 với mọi x \(\ge\) 0)
\(\Leftrightarrow\) \(\dfrac{6}{2\left(x+1\right)}\ge\dfrac{3\sqrt{x}}{x+1}\)
\(\Leftrightarrow\) \(\dfrac{3}{x+1}\ge\dfrac{3\sqrt{x}}{x+1}\) (*)
Dấu "=" xảy ra \(\Leftrightarrow\) x = 1 (TM)
Khi đó: \(\dfrac{3\sqrt{x}}{x+1}\le\dfrac{3}{1+1}=\dfrac{3}{2}\)
Vậy QMax = \(\dfrac{3}{2}\) khi và chỉ khi x = 1
Chúc bn học tốt!

1) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot10=6\cdot8=48\)
hay AH=4,8(cm)




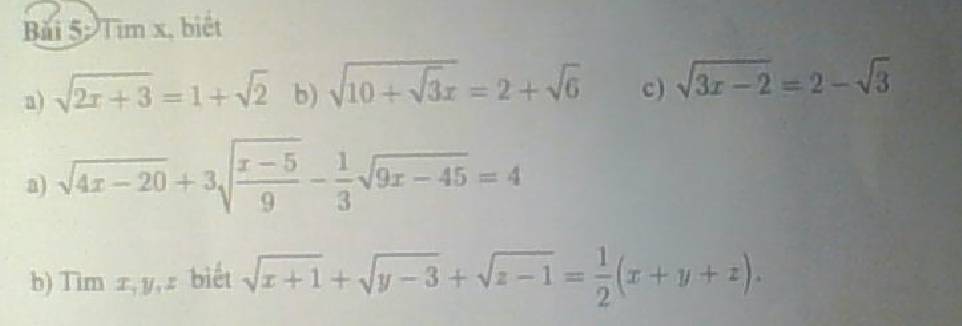



 Mn giúp mình bài 3 với ạ. Mình đang cần gấp lắm. Mình cảm ơn nhiều !
Mn giúp mình bài 3 với ạ. Mình đang cần gấp lắm. Mình cảm ơn nhiều !
Lời giải:
Đặt \(\sqrt[3]{5\sqrt{2}+7}=m; \sqrt[3]{5\sqrt{2}-7}=n\)
\(m^3-n^3=14\)
\(mn=1\)
\((a+b+c)^3=(m-n)^3=m^3-3mn(m-n)-n^3=14-3(m-n)\)
\(\Leftrightarrow (a+b+c)^3=14-3(a+b+c)\)
\(\Leftrightarrow (a+b+c)^3+3(a+b+c)-14=0\)
\(\Leftrightarrow (a+b+c)^2[(a+b+c)-2]+2(a+b+c)(a+b+c-2)+7(a+b+c-2)=0\)
\(\Leftrightarrow (a+b+c-2)[(a+b+c)^2+2(a+b+c)+7]=0\)
Dễ thấy biểu thức trong ngoặc vuông $>0$ nên $a+b+c-2=0$
$\Leftrightarrow a+b+c=2$
$ab+bc+ac=\frac{(a+b+c)^2-(a^2+b^2+c^2)}{2}=\frac{2^2-1}{2}=\frac{3}{2}$