
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


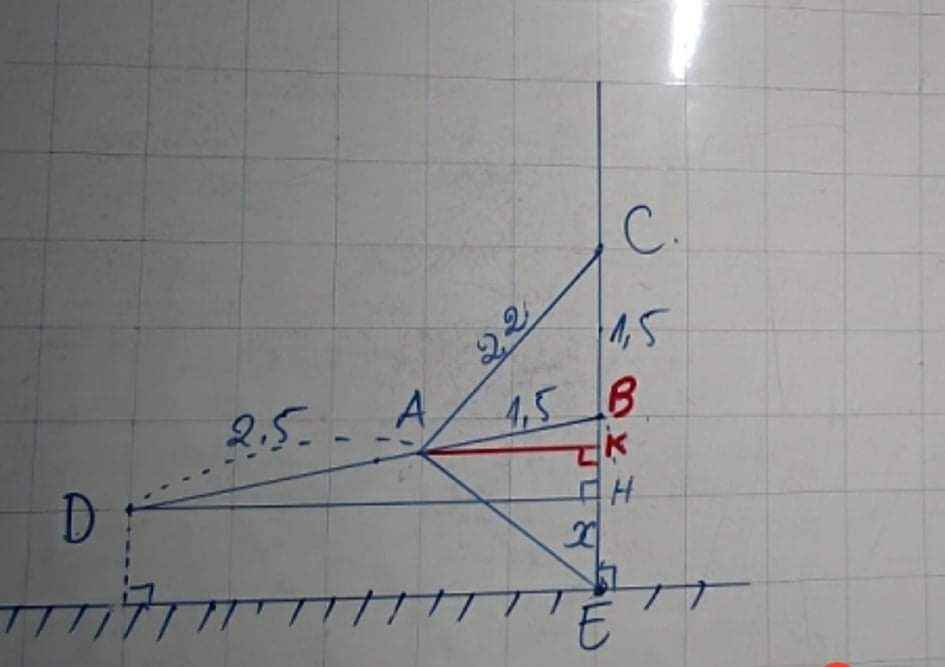
C A B E D H K
Gọi DH là khoảng cách thấp nhất từ máy bay đến mặt đất, khi đó AC có độ dài lớn nhất là 2,2m. Dựng hình chữ nhật DHEK => DH = EK
Do BA = BE = BC = 1,5m cố định nên tam giác ACE vuông tại A
Xét tam giác ACE vuông tại A có cos\(\widehat{ECA}\) = \(\dfrac{CA}{CE}=\dfrac{2,2}{3}\) => \(\widehat{ECA}\) \(\approx\) 42o50'
BA = BC => tam giác ABC cân tại B => \(\widehat{BAC}=\widehat{BCA}\) = \(\widehat{ECA}\) \(\approx\) 42o50'
=> \(\widehat{DBK}\) = \(\widehat{BAC}+\widehat{BCA}\) = 2.\(\widehat{BCA}\) = 85o40'
Xét tam giác DBK vuông tại D có: BK = BD. cos\(\widehat{DBK}\)
= 4.cos85o40' \(\approx\) 0,3022
=> DH = KE \(\approx\) 1,5 - 0,3022 \(\approx\)1,2 (m)

\(g,ĐK:x\ge0\\ PT\Leftrightarrow10\sqrt{x}+8\sqrt{x}-11\sqrt{x}=21\\ \Leftrightarrow\sqrt{x}=3\Leftrightarrow x=9\left(tm\right)\\ h,ĐK:x\ge0\\ PT\Leftrightarrow6\sqrt{3x}+2\sqrt{3x}-3\sqrt{3x}=15\\ \Leftrightarrow\sqrt{3x}=5\Leftrightarrow3x=25\Leftrightarrow x=\dfrac{25}{3}\left(tm\right)\\ i,ĐK:x\ge0\\ PT\Leftrightarrow12\sqrt{x}-21-2\sqrt{x}+10=6\sqrt{x}-12\\ \Leftrightarrow4\sqrt{x}=-1\Leftrightarrow\sqrt{x}=-\dfrac{1}{4}\Leftrightarrow x\in\varnothing\\ j,ĐK:x\ge2\\ PT\Leftrightarrow6\sqrt{x-2}-15\cdot\dfrac{1}{5}\sqrt{x-2}=20+4\sqrt{x-2}\\ \Leftrightarrow\sqrt{x-2}=-20\Leftrightarrow x\in\varnothing\)
\(k,ĐK:x\ge3\\ PT\Leftrightarrow6\sqrt{x-3}-\dfrac{1}{5}\cdot5\sqrt{x-3}-\dfrac{1}{7}\cdot7\sqrt{x-3}=20\\ \Leftrightarrow4\sqrt{x-3}=20\Leftrightarrow\sqrt{x-3}=5\\ \Leftrightarrow x-3=25\Leftrightarrow x=28\left(tm\right)\\ l,ĐK:x\ge5\\ PT\Leftrightarrow2\sqrt{x-5}+\sqrt{x-5}-\dfrac{1}{3}\cdot3\sqrt{x-5}=4\\ \Leftrightarrow2\sqrt{x-5}=4\Leftrightarrow\sqrt{x-5}=2\\ \Leftrightarrow x-5=4\Leftrightarrow x=9\left(tm\right)\)

Lời giải:
Đặt \(\sqrt[3]{5\sqrt{2}+7}=m; \sqrt[3]{5\sqrt{2}-7}=n\)
\(m^3-n^3=14\)
\(mn=1\)
\((a+b+c)^3=(m-n)^3=m^3-3mn(m-n)-n^3=14-3(m-n)\)
\(\Leftrightarrow (a+b+c)^3=14-3(a+b+c)\)
\(\Leftrightarrow (a+b+c)^3+3(a+b+c)-14=0\)
\(\Leftrightarrow (a+b+c)^2[(a+b+c)-2]+2(a+b+c)(a+b+c-2)+7(a+b+c-2)=0\)
\(\Leftrightarrow (a+b+c-2)[(a+b+c)^2+2(a+b+c)+7]=0\)
Dễ thấy biểu thức trong ngoặc vuông $>0$ nên $a+b+c-2=0$
$\Leftrightarrow a+b+c=2$
$ab+bc+ac=\frac{(a+b+c)^2-(a^2+b^2+c^2)}{2}=\frac{2^2-1}{2}=\frac{3}{2}$

a: Ta có: BC⊥BA tại B
nên BC là tiếp tuyến của (A;AB)
b: Xét (A) có
CB là tiếp tuyến
CD là tiếp tuyến
Do đó: CB=CD
hay C nằm trên đường trung trực của BD(1)
Ta có: AB=AD
nên A nằm trên đường trung trực của BD(2)
Từ (1) và (2) suy ra AC là đường trung trực của BD
hay AC\(\perp\)BD
Giúp mình luôn câu c d được không:((( sắp hết h rồi mà không bt làm

Q = \(\dfrac{3\sqrt{x}}{x+1}\) (x \(\ge\) 0; x \(\ne\) 4)
Áp dụng BĐT Cô-si cho 2 số không âm x và 1 ta được:
\(\dfrac{x+1}{2}\ge\sqrt{x}\) (1)
\(\Leftrightarrow\) \(\dfrac{3\cdot\dfrac{x+1}{2}}{x+1}\ge\dfrac{3\sqrt{x}}{x+1}\) (x + 1 > 0 với mọi x \(\ge\) 0)
\(\Leftrightarrow\) \(\dfrac{6}{2\left(x+1\right)}\ge\dfrac{3\sqrt{x}}{x+1}\)
\(\Leftrightarrow\) \(\dfrac{3}{x+1}\ge\dfrac{3\sqrt{x}}{x+1}\) (*)
Dấu "=" xảy ra \(\Leftrightarrow\) x = 1 (TM)
Khi đó: \(\dfrac{3\sqrt{x}}{x+1}\le\dfrac{3}{1+1}=\dfrac{3}{2}\)
Vậy QMax = \(\dfrac{3}{2}\) khi và chỉ khi x = 1
Chúc bn học tốt!


a: \(VT=\left(\dfrac{\sqrt{7}\left(\sqrt{2}-1\right)}{2\left(\sqrt{2}-1\right)}+\dfrac{\sqrt{5}\left(\sqrt{3}-1\right)}{2\left(\sqrt{3}-1\right)}\right)\cdot\left(\sqrt{7}-\sqrt{5}\right)\)
\(=\left(\dfrac{\sqrt{7}+\sqrt{5}}{2}\right)\cdot\left(\sqrt{7}-\sqrt{5}\right)=\dfrac{7-5}{2}=\dfrac{2}{2}=1\)
=VP
b: \(VT=3-\sqrt{5}+2\left(\sqrt{5}+1\right)-\left|\sqrt{5}-2\right|\)
=3-căn 5+2căn 5+2-căn 5+2
=3+2+2=7
=VP

5:
a: =>2x+3=3+2căn 2
=>2x=2căn 2
=>x=căn 2
b: =>10+căn 3x=10+4căn 6
=>căn 3x=4căn 6=căn 96
=>3x=96
=>x=32
c: =>3x-2=7-4căn 3
=>3x=9-4căn 3
=>x=3-4/3*căn 3
a: =>\(2\cdot\sqrt{x-5}+\sqrt{x-5}-\sqrt{x-5}=4\)
=>2*căn x-5=4
=>căn x-5=2
=>x-5=4
=>x=9

a: Xét ΔSBM và ΔSNB có
\(\widehat{SBM}=\widehat{SNB}\)
\(\widehat{BSM}\) chung
Do đó: ΔSBM\(\sim\)ΔSNB
Suy ra: SB/SN=SM/SB
hay \(SB^2=SM\cdot SN\)
b: Xét (O) có
SA là tiếp tuyến
SB là tiếp tuyến
Do đó: SA=SB
mà OA=OB
nên SO là đường trung trực của AB
=>SO⊥AB
Xét ΔOBS vuông tại B có BH là đường cao
nên \(SH\cdot SO=SB^2=SM\cdot SN\)


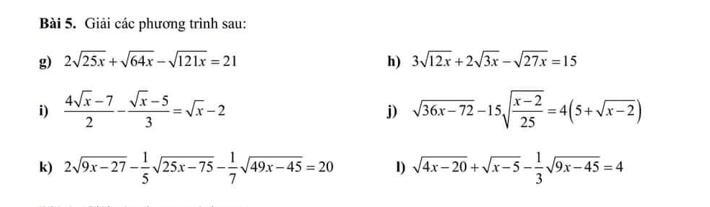



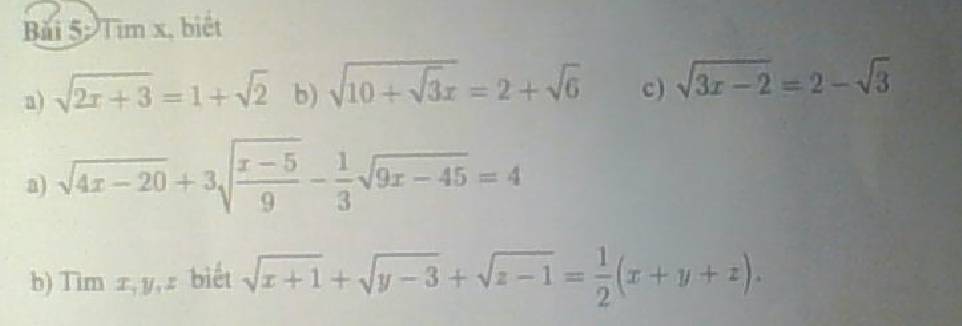


Câu 1 :
a, \(A=\left(\frac{1}{\sqrt{a}-1}+\frac{1}{\sqrt{a}+1}\right).\frac{1}{\sqrt{a}}\)
\(=\left(\frac{\sqrt{a}+1}{a-1}+\frac{\sqrt{a}-1}{a-1}\right).\frac{1}{\sqrt{a}}=\frac{2\sqrt{a}}{a-1}.\frac{1}{\sqrt{a}}=\frac{2}{a-1}\)
b, Ta có :A = 1 hay \(\frac{2}{a-1}=1\Leftrightarrow a-1=2\Leftrightarrow a=3\)( tmđkxđ )
Câu 3 :
\(\hept{\begin{cases}2x-3y=1\left(1\right)\\3x+y=7\left(2\right)\end{cases}}\)Ta có : \(y=7-3x\)(k)
Thay vào phương trình 1 ta được :
\(2x-3\left(7-3x\right)=1\)
\(\Leftrightarrow2x-21+9x=1\Leftrightarrow11x=22\Leftrightarrow x=2\)
Thay vào (k) ta được : \(y=7-3.2=7-6=1\)
Vậy \(\left\{x;y\right\}=\left\{2;1\right\}\)