
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{5}=\dfrac{b}{2}=\dfrac{2a-3b}{2\cdot5-3\cdot2}=\dfrac{12}{4}=3\)
Do đó: a=15; b=6
d) Áp dụng t/c dtsbn:
\(\dfrac{a}{5}=\dfrac{b}{2}=\dfrac{2a}{10}=\dfrac{3b}{6}=\dfrac{2a-3b}{10-6}=\dfrac{12}{4}=3\)
\(\Rightarrow\left\{{}\begin{matrix}a=3.5=15\\b=3.2=6\end{matrix}\right.\)
f) \(\Rightarrow\dfrac{x}{5}=\dfrac{y}{3}=-\dfrac{z}{2}\)
Áp dụng t/c dtsbn:
\(\dfrac{x}{5}=\dfrac{y}{3}=\dfrac{-z}{2}=\dfrac{x+y-z}{5+3+2}=\dfrac{2}{10}=\dfrac{1}{5}\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{1}{5}.5=1\\y=\dfrac{1}{5}.3=\dfrac{3}{5}\\z=\dfrac{1}{5}.\left(-2\right)=-\dfrac{2}{5}\end{matrix}\right.\)
g) \(\dfrac{x}{4}=\dfrac{y}{5}=k\)\(\Rightarrow\left\{{}\begin{matrix}x=4k\\y=5k\end{matrix}\right.\)
\(\Rightarrow xy=20k^2=500\Rightarrow k=\pm5\)
\(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=20\\y=25\end{matrix}\right.\\\left\{{}\begin{matrix}x=-20\\y=-25\end{matrix}\right.\end{matrix}\right.\)

4:
a: \(\dfrac{31}{23}-\left(\dfrac{7}{32}+\dfrac{8}{23}\right)\)
\(=\dfrac{31}{23}-\dfrac{7}{32}-\dfrac{8}{23}\)
\(=1-\dfrac{7}{32}=\dfrac{25}{32}\)
b: \(\left(\dfrac{1}{3}+\dfrac{12}{67}+\dfrac{13}{41}\right)-\left(\dfrac{79}{67}-\dfrac{28}{41}\right)\)
\(=\dfrac{1}{3}+\dfrac{12}{67}+\dfrac{13}{41}-\dfrac{79}{67}+\dfrac{28}{41}\)
\(=\dfrac{1}{3}+1-1=\dfrac{1}{3}\)
c: \(\left(-30,75\right)+\left(\dfrac{31}{10}-69,25\right)-\left(-6,9\right)\)
\(=-30,75+3,1-69,25+6,9\)
=10-100
=-90
d: \(\left(-34,5\right)\cdot\dfrac{11}{25}-65,5\cdot\dfrac{11}{25}\)
\(=\dfrac{11}{25}\left(-34,5-65,5\right)\)
\(=\dfrac{11}{25}\cdot\left(-100\right)=-44\)
Bài 1:
a: \(\dfrac{1}{6}-0,4\cdot\dfrac{5}{8}+\dfrac{1}{2}\)
\(=\dfrac{1}{6}-\dfrac{2}{5}\cdot\dfrac{5}{8}+\dfrac{1}{2}\)
\(=\dfrac{1}{6}-\dfrac{1}{4}+\dfrac{1}{2}=\dfrac{2-3+6}{12}=\dfrac{5}{12}\)
b: \(\left(-\dfrac{2}{3}\right)^2+\dfrac{1}{6}-\left(-0,5\right)^3\)
\(=\dfrac{4}{9}+\dfrac{1}{6}+\dfrac{1}{8}\)
\(=\dfrac{32+12+9}{72}=\dfrac{53}{72}\)


2:
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
b: BA=BE
DA=DE
=>BD là trung trực của AE
c: DA=DE
DE<DC
=>DA<DC
4:
a: ΔABC cân tại A có AI là phân giác
nên AI vuông góc BC tại I
b: Xét ΔABC có
CM,AI là trung tuyến
CM cắt AI tại G
=>G là trọng tâm
=>BG là trung tuyến của ΔABC
c: BI=CI=9cm
=>AI=căn 15^2-9^2=12cm
=>GI=1/3*12=4cm



a: Xét ΔABE và ΔADC có
AB=AD
\(\widehat{BAE}=\widehat{DAC}\)
AE=AC
Do đó: ΔABE=ΔADC

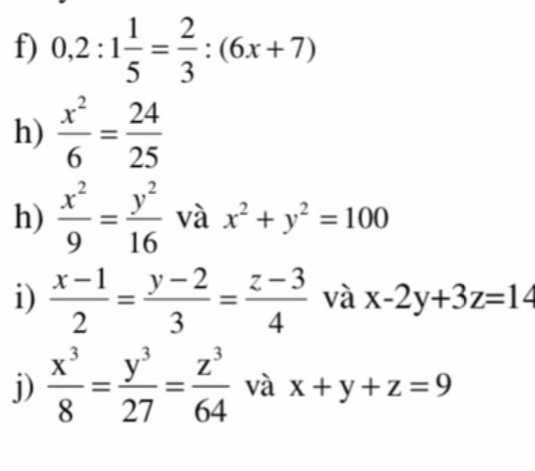
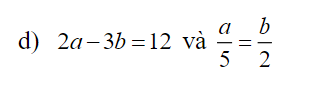
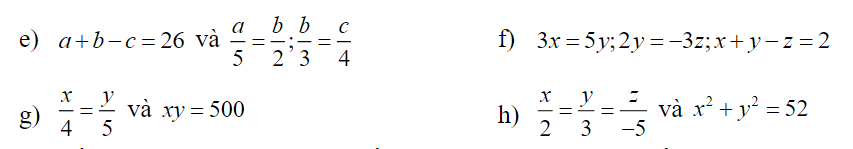



 GIÚP MÌNH VỚI Ạ MÌNH ĐANG CẦN GẤP Ạ MINH CẢM ƠN RẤT NHIỀU
GIÚP MÌNH VỚI Ạ MÌNH ĐANG CẦN GẤP Ạ MINH CẢM ƠN RẤT NHIỀU

h: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x^2}{9}=\dfrac{y^2}{16}=\dfrac{x^2+y^2}{9+16}=\dfrac{100}{25}=4\)
Do đó: \(\left\{{}\begin{matrix}x\in\left\{6;-6\right\}\\y\in\left\{8;-8\right\}\end{matrix}\right.\)