
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





1: Xét ΔCEH vuông tại E và ΔCAB vuông tại A có
góc C chung
=>ΔCEH đồng dạng vớiΔCAB
2: góc HEB+góc HAB=180 độ
=>HEBA nội tiếp
=>góc HBC=góc EAC
3: Xét ΔIHE và ΔIAB có
góc IHE=góc IAB
góc HIE=góc AIB
=>ΔIHE đồng dạng với ΔIAB
=>HE/AB=IH/IA
=>HE*IA=IH*AB


3.(⅓x - ¼)² = ⅓
=> (\(\dfrac{1}{3x}\)- \(\dfrac{1}{4}\) )2 = \(\dfrac{1}{9}\)
=>\(\left[{}\begin{matrix}\dfrac{1}{3x}-\dfrac{1}{4}=\dfrac{-1}{3}\\\dfrac{1}{3x}-\dfrac{1}{4}=\dfrac{1}{3}\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}\dfrac{1}{3x}=\dfrac{-1}{12}\\\dfrac{1}{3x}=\dfrac{7}{12}\end{matrix}\right.\) => \(\left[{}\begin{matrix}x=-4\\x=\dfrac{12}{21}=\dfrac{4}{7}\end{matrix}\right.\)
Vậy, tập nghiệm x thỏa mãn là S=\(\left\{-4;\dfrac{4}{7}\right\}\)

`(x+3)(x^2-5x+8)=(x+3).x^2`
`<=>(x+3)(x^2-5x+8-x^2)=0`
`<=>(x+3)(8-5x)=0`
`<=>` \(\left[ \begin{array}{l}x+3=0\\8-5x=0\end{array} \right.\)
`<=>` \(\left[ \begin{array}{l}x=\dfrac85\\x=-3\end{array} \right.\)
Vậy `S={-3,8/5}`
`(x+3)(x^2-5x+8)=(x+3).x^2`
`<=>(x+3)(x^2-5x+8-x^2)=0`
`<=>(x+3)(-5x+8)=0`
\(\Leftrightarrow\left[{}\begin{matrix}x+3=0\\-5x+8=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=-3\\x=\dfrac{8}{5}\end{matrix}\right.\)
Vậy `S={-3;8/5}`.

\(\Leftrightarrow2\left(x+1\right)^3=56\Leftrightarrow\left(x+1\right)^3=28\Leftrightarrow\)
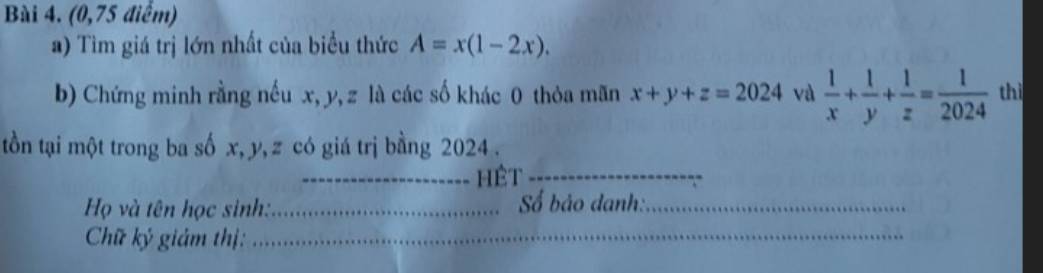









a.
\(A=x\left(1-2x\right)=-2x^2+x=-2\left(x-\dfrac{1}{2}\right)^2+\dfrac{1}{8}\le\dfrac{1}{8}\)
\(A_{max}=\dfrac{1}{8}\) khi \(x=\dfrac{1}{2}\)
b.
\(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=\dfrac{1}{x+y+z}\) (do \(x+y+z=2024\))
\(\Rightarrow\dfrac{x+y}{xy}+\dfrac{1}{z}-\dfrac{1}{x+y+z}=0\)
\(\Rightarrow\dfrac{x+y}{xy}+\dfrac{x+y}{z\left(x+y+z\right)}=0\)
\(\Rightarrow\left(x+y\right)\left(\dfrac{1}{xy}+\dfrac{1}{z\left(x+y+z\right)}\right)=0\)
\(\Rightarrow\left(x+y\right)\left(\dfrac{xy+xz+yz+z^2}{xyz\left(x+y+z\right)}\right)=0\)
\(\Rightarrow\left(x+y\right)\left(\dfrac{x\left(y+z\right)+z\left(y+z\right)}{xyz\left(x+y+z\right)}\right)=0\)
\(\Rightarrow\dfrac{\left(x+y\right)\left(y+z\right)\left(x+z\right)}{xyz\left(x+y+z\right)}=0\)
\(\Rightarrow\left(x+y\right)\left(y+z\right)\left(x+z\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x+y=0\\y+z=0\\x+z=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x+y+z=z\\x+y+z=x\\x+y+z=y\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}2024=z\\2024=x\\2024=y\end{matrix}\right.\) (đpcm)