
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: ĐKXĐ: \(x\notin\left\{10;-10;\sqrt{10};-\sqrt{10}\right\}\)
b: \(A=\dfrac{5x^3+50x+2x^2+20+5x^3-50x-2x^2+20}{\left(x^2-10\right)\left(x^2+10\right)}\cdot\dfrac{x^2-100}{x^2+4}\)
\(=\dfrac{10x^3+40}{\left(x^2-10\right)\left(x^2+10\right)}\cdot\dfrac{x^2-100}{x^2+4}\)

a: Xét tứ giác BHCD có
BH//CD
CH//BD
Do đó: BHCD là hình bình hành

1: Xét tứ giác BHCK có
CH//BK
BH//CK
Do đó: BHCK là hình bình hành
Suy ra: Hai đường chéo BC và HK cắt nhau tại trung điểm của mỗi đường
mà M là trung điểm của BC
nên M là trung điểm của HK
2: Gọi giao điểm của IH và BC là O
Suy ra: IH\(\perp\)BC tại O và O là trung điểm của IH
Xét ΔHIK có
O là trung điểm của HI
M là trung điểm của HK
Do đó: OM là đường trung bình của ΔHIK
Suy ra: OM//IK
hay BC//IK
mà BC\(\perp\)IH
nên IH\(\perp\)IK
Xét ΔHOC vuông tại O và ΔIOC vuông tại O có
OC chung
HO=IO
Do đó: ΔHOC=ΔIOC
Suy ra: CH=CI
mà CH=BK
nên CI=BK
Xét tứ giác BCKI có IK//BC
nên BCKI là hình thang
mà CI=BK
nên BCKI là hình thang cân

a) \(x^2-6x+10=\left(x^2-6x+9\right)+1\)
\(=\left(x-3\right)^2+1\ge1>0\forall x\)
b) \(4x-x^2-5=-\left(x^2-4x+4\right)-1\)
\(=-\left(x-2\right)^2-1\le-1< 0\forall x\)





a, Với x khác -3 ; 3
\(B=\dfrac{6+5x+15+x-3}{\left(x-3\right)\left(x+3\right)}=\dfrac{6x+18}{\left(x-3\right)\left(x+3\right)}=\dfrac{6}{x-3}\)
vậy ta có đpcm
b, Thay x = 4 vào B ta được \(\dfrac{6}{4-3}=6\)
c, \(\Rightarrow x-3\inƯ\left(6\right)=\left\{\pm1;\pm2;\pm3;\pm6\right\}\)
| x-3 | 1 | -1 | 2 | -2 | 3 | -3 | 6 | -6 |
| x | 4 | 2 | 5 | 1 | 6 | 0 | 9 | -3(loại) |

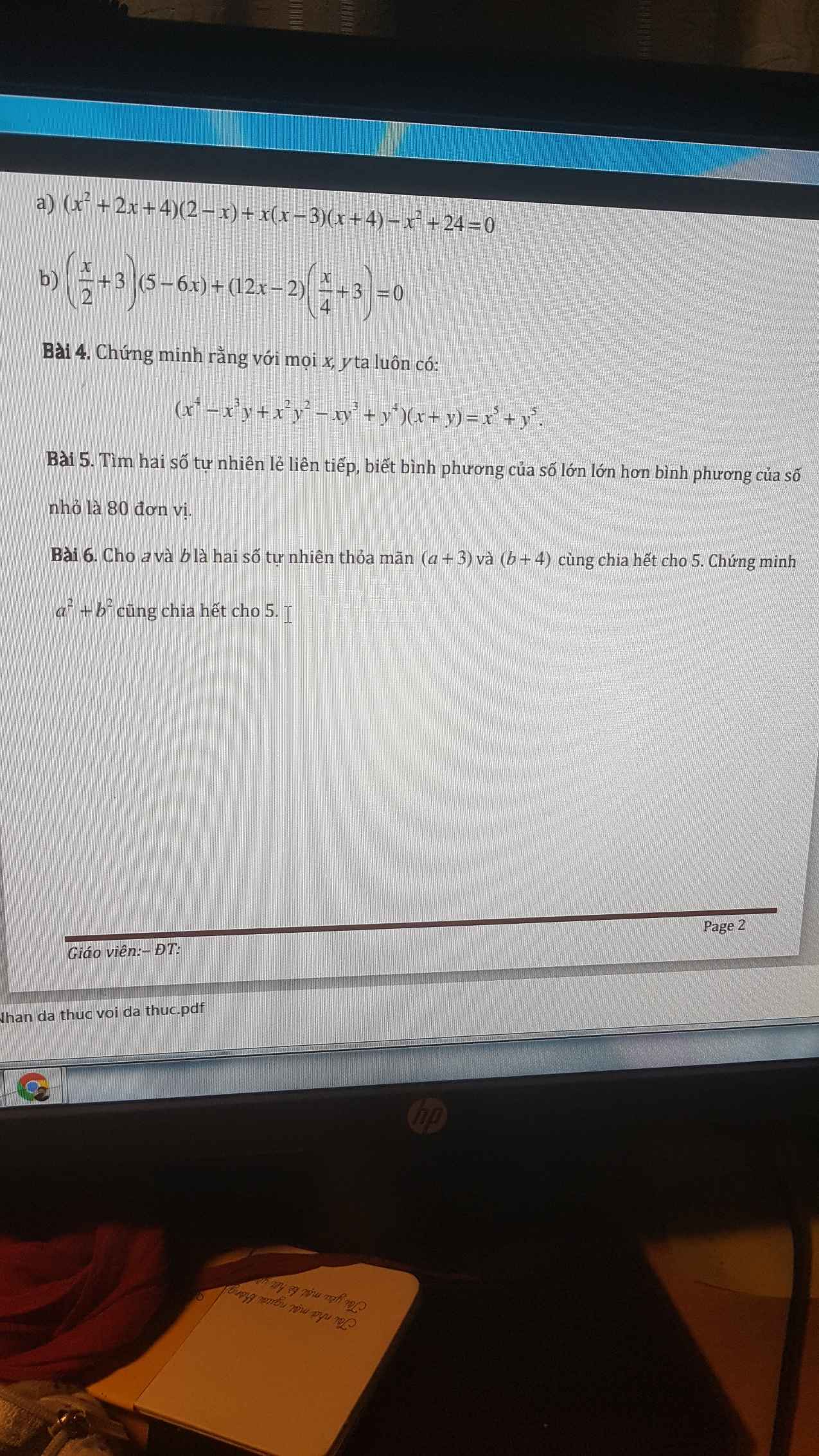
 Các bạn giải giúp mình với ạ, phần a ghi chi tiết bước giải hộ mình nhé. Mình cám ơn ạ! (Mai mình nộp rồi nên nhanh giúp mình ạ T.T)
Các bạn giải giúp mình với ạ, phần a ghi chi tiết bước giải hộ mình nhé. Mình cám ơn ạ! (Mai mình nộp rồi nên nhanh giúp mình ạ T.T)






Trước hết ta sẽ chứng minh: \(\dfrac{x^2}{a}+\dfrac{y^2}{b}\ge\dfrac{\left(x+y\right)^2}{a+b}\)(1)
Ta có (1) tương đương với:
\(x^2b\left(a+b\right)+y^2a\left(a+b\right)\ge\left(x+y\right)^2ab\)
\(\Leftrightarrow\left(xb-ya\right)^2\ge0\) (luôn đúng)
Dấu \(=\) xảy ra khi \(xb=ya\Leftrightarrow\dfrac{x}{a}=\dfrac{y}{b}\).
Áp dụng bất đẳng thức (1) ta có:
\(\dfrac{x^2}{a}+\dfrac{y^2}{b}+\dfrac{z^2}{c}\ge\dfrac{\left(x+y\right)^2}{a+b}+\dfrac{z^2}{c}\ge\dfrac{\left(x+y+z\right)^2}{a+b+c}\)
Dấu \(=\) xảy ra khi \(\dfrac{x}{a}=\dfrac{b}{y}=\dfrac{z}{c}\).