
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



1: A=-1/2*xy^3*4x^2y^2=-2x^3y^5
Bậc là 8
Phần biến là x^3;y^5
Hệ số là -2
2:
a: P(x)=3x+4x^4-2x^3+4x^2-x^4-6
=3x^4-2x^3+4x^2+3x-6
Q(x)=2x^4+4x^2-2x^3+x^4+3
=3x^4-2x^3+4x^2+3
b: A(x)=P(x)-Q(x)
=3x^4-2x^3+4x^2+3x-6-3x^4+2x^3-4x^2-3
=3x-9
A(x)=0
=>3x-9=0
=>x=3


a) Xét ΔOBH và ΔODA có
OB=OD(gt)
\(\widehat{BOH}=\widehat{DOA}\)(hai góc đối đỉnh)
OH=OA(O là trung điểm của HA)
Do đó: ΔOBH=ΔODA(c-g-c)
Suy ra: \(\widehat{OHB}=\widehat{OAD}\)(hai góc tương ứng)
mà \(\widehat{OHB}=90^0\)(gt)
nên \(\widehat{OAD}=90^0\)
hay AH\(\perp\)AD(đpcm)
b) Xét ΔAOE vuông tại A và ΔHOC vuông tại H có
OA=OH(O là trung điểm của AH)
\(\widehat{AOE}=\widehat{HOC}\)(hai góc đối đỉnh)
Do đó: ΔAOE=ΔHOC(Cạnh góc vuông-góc nhọn kề)
Suy ra: AE=HC(hai cạnh tương ứng)(1)
Ta có: ΔAOD=ΔHOB(cmt)
nên AD=HB(Hai cạnh tương ứng)(2)
Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC(ΔABC cân tại A)
AH chung
Do đó: ΔAHB=ΔAHC(Cạnh huyền-cạnh góc vuông)
Suy ra: HB=HC(Hai cạnh tương ứng)(3)
Từ (1), (2) và (3) suy ra AD=AE
mà E,A,D thẳng hàng(gt)
nên A là trung điểm của DE
) Xét ΔOBH và ΔODA có
OB=OD(gt)
ˆBOH=ˆDOABOH^=DOA^(hai góc đối đỉnh)
OH=OA(O là trung điểm của HA)
Do đó: ΔOBH=ΔODA(c-g-c)
Suy ra: ˆOHB=ˆOADOHB^=OAD^(hai góc tương ứng)
mà ˆOHB=900OHB^=900(gt)
nên ˆOAD=900OAD^=900
hay AH⊥⊥AD(đpcm)
b) Xét ΔAOE vuông tại A và ΔHOC vuông tại H có
OA=OH(O là trung điểm của AH)
ˆAOE=ˆHOCAOE^=HOC^(hai góc đối đỉnh)
Do đó: ΔAOE=ΔHOC(Cạnh góc vuông-góc nhọn kề)
Suy ra: AE=HC(hai cạnh tương ứng)(1)
Ta có: ΔAOD=ΔHOB(cmt)
nên AD=HB(Hai cạnh tương ứng)(2)
Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC(ΔABC cân tại A)
AH chung
Do đó: ΔAHB=ΔAHC(Cạnh huyền-cạnh góc vuông)
Suy ra: HB=HC(Hai cạnh tương ứng)(3)
Từ (1), (2) và (3) suy ra AD=AE
mà E,A,D thẳng hàng(gt)
nên A là trung điểm của DE

Bài 3:
a) Ta có: \(A-\left(9x^3+8x^2-2x-7\right)=-9x^3-8x^2+5x+11\)
\(\Leftrightarrow A=-9x^3-8x^2+5x+11+9x^3+8x^2-2x-7\)
\(\Leftrightarrow A=3x+4\)
b) Đặt A(x)=0
nên 3x+4=0
hay \(x=-\dfrac{4}{3}\)
Bạn có biết giải bài hình k giúp mình với 21:00 mình phải nộp rồi

Câu 4:
a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
Câu 1:
\(a,=\dfrac{1}{2}+9\cdot\dfrac{1}{9}-18=\dfrac{1}{2}+1-18=-\dfrac{33}{2}\\ b,=2-1+4\cdot\dfrac{1}{4}+9\cdot\dfrac{1}{9}\cdot9=1+1+9=11\\ c,=-21,3\left(54,6+45,4\right)=-21,3\cdot100=-2130\\ d,B=\left(\dfrac{1}{16}+\dfrac{1}{2}-\dfrac{1}{16}\right):\left(\dfrac{1}{8}-\dfrac{1}{8}+1\right)=\dfrac{1}{2}:1=\dfrac{1}{2}\)

1)
a. Xét tg ABC cân tại A có AC=AB; gACB = g ABC.
Xét tg ACN và tg ABM có:
CN=BM (gt)
AC=AB
gACB=gABC
=> tg ACN = tg ABM (cgc)
=> AN=AM (2 cạnh tg ứng)
H là trung điểm BC nên AH là đường trung tuyến của tg ABC
Mak tg ABC cân => H cũng là đường cao của tg ABC => AH ⊥ BC
b. Vì H là trung đ của BC nên CH=HB=BC/2= 3cm
Áp dụng định lý Py ta go vào tg AHB có:
AB^2=AH^2+HB^2
AH^2= AB^2 - HB^2
AH^2= 5^2 - 3^2 = 16 cm
=> AH= 4 cm
c. Xét tg AMN và tg KMB có:
AM=KM (gt)
MN=BM (gt)
gHMA=gKMB (đối đỉnh)
=> tg AMN = tg KMB (cgc)
d. tg AMN = tg KMB => gMAN=gMKB
=> AN=KB=Am
Mà AB>AM (quan hệ giữ đường xiêng và hình chiếu) nên AB>BK
=> gBKA> gBAK
=> gMAN>gBAM

a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
AB=AC
\(\widehat{BAD}\) chung
Do đó: ΔABD=ΔACE
Suy ra: BD=CE
b: Xét ΔEBC vuông tại E và ΔDCB vuông tại D có
BC chung
EC=DB
Do đó:ΔEBC=ΔDCB
Suy ra: \(\widehat{KCB}=\widehat{KBC}\)
hay ΔKBC cân tại K
d: Xét ΔABK và ΔACK có
AB=AC
BK=CK
AK chung
Do đó: ΔABK=ΔACK
Suy ra: \(\widehat{BAK}=\widehat{CAK}\)
hay AK là tia phân giác của góc BAC
 giúp mình với, mk cần gấp ạ, cảm ơn mn rất nhìu !
giúp mình với, mk cần gấp ạ, cảm ơn mn rất nhìu !
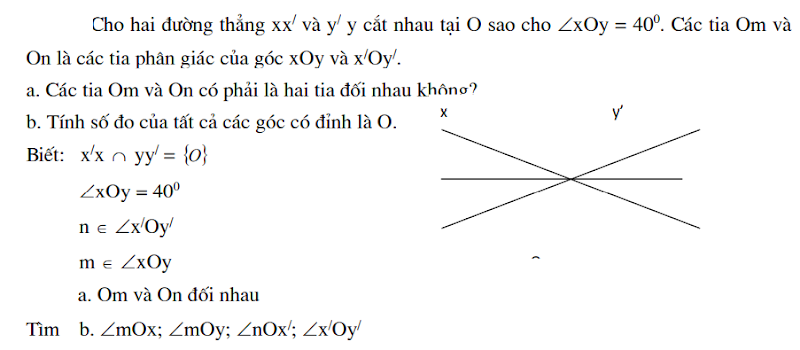 giúp mình vs nha cảm ơn mn nhìu
giúp mình vs nha cảm ơn mn nhìu




\(f\left(-2\right)=-3.\left(-2\right)+5\frac{3}{5}+\frac{-4}{3}+\frac{-3}{5}=9\frac{2}{3}\)
\(f\left(\frac{1}{3}\right)=-3.\frac{1}{3}+5\frac{3}{5}+\frac{-4}{3}+\frac{-3}{5}=2\frac{2}{3}\)
2)\(f\left(x\right)=3x+3\frac{2}{3}=10\)
\(3x=10-3\frac{2}{3}\)
\(x=\frac{19}{3}:3\)
\(x=\frac{19}{9}\)
3)\(\frac{\left(x-2\right)^3}{8}=\frac{-27}{64}?\frac{3}{5}+\frac{-4}{3}+\frac{-3}{5}\)