Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét tứ giác ABCD có:
\(\begin{array}{l} \widehat A + \widehat B + \widehat C + \widehat D = {360^0}\\{85^0} + x + {65^0} + {75^0} = {360^0}\\x = {360^0} - {85^0} - {65^0} - {75^0} = {135^0}\end{array}\)

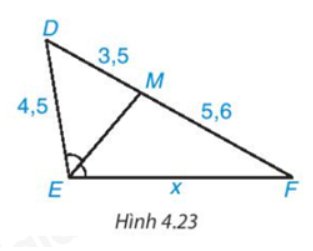
Trong Hình 4.23 có \(\widehat {DME} = \widehat {MEF}\) nên EM là tia phân giác của \(\widehat {{\rm{DEF}}}\).
Áp dụng tính chất đường phân giác của tam giác, ta có:
\(\dfrac{{E{\rm{D}}}}{{EF}} = \dfrac{{M{\rm{D}}}}{{MF}}\) hay \(\dfrac{{4,5}}{x} = \dfrac{{3,5}}{{5,6}}\)
Suy ra: \(x = \dfrac{{5,6.4,5}}{{3,5}} = 7,2\)(đvđd)
Vậy x = 7,2 (đvđd).

với đa thức bậc 2 ax2 + bx + c bạn tách thành ax2 + mx + nx + c sao cho m + n = b và mn = ac
còn 1 phương pháp nữa đó là tìm nghiệm.
nếu đa thức có nghiệm là x1, x2,...xn thì sẽ phân tích đc thành (x - x1)(x - x2)...(x - xn)

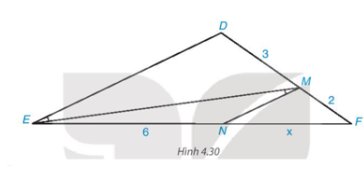
Trong Hình 4.30 có \(\widehat {DEM} = \widehat {EMN}\) mà hai góc này ở vị trí so le trong nên MN // DE.
Áp dụng định lí Thalès vào tam giác DEF có MN // DE, ta có:
\(\dfrac{{MF}}{{M{\rm{D}}}} = \dfrac{{NF}}{{NE}}\) hay \(\dfrac{2}{3} = \dfrac{x}{6}\)
Suy ra \(x = \dfrac{{2.6}}{3} = 4\) (đvđd).
Vậy x = 4 (đvđd).

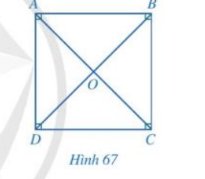
Do tứ giác ABCD là hình vuông \(\Rightarrow\widehat{CAB}=\widehat{DAC}=\dfrac{\widehat{BAD}}{2}=\dfrac{90^o}{2}=45^o\)

a: Xét tứ giác DIHK có
góc DIH=góc DKH=góc KDI=90 độ
nên DIHK là hình chữ nhật
b: Xét tứ giác IHAK có
IH//AK
IH=AK
Do đó: IHAK là hình bình hành
=>B là trung điểm chung của IA và HK
Xét ΔIKA có IC/IK=IB/IA
nên BC//KA
Xét ΔIDA có IB/IA=IM/ID
nên BM//DA
=>B,C,M thẳng hàng
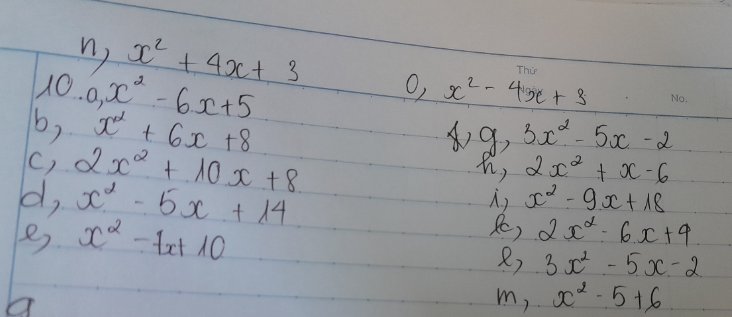






`n)x^2+4x+3`
`=x^2+3x+x+3`
`=x(x+3)+(x+3)`
`=(x+3)(x+1)`
`b)x^2+6x+8`
`=x^2+4x+2x+8`
`=x(x+4)+2(x+4)`
`=(x+4)(x+2)`
`->` tách ra nha bạn
\(10,\\ a,x^2-6x+5\\ =x^2-x-5x+5\\ =x\left(x-1\right)-5\left(x-1\right)\\ =\left(x-1\right)\left(x-5\right)\)
\(b,x^2+6x+8\\ =x^2+4x+2x+8\\ =x\left(x+4\right)+2\left(x+4\right)\\ =\left(x+4\right)\left(x+2\right)\)
\(c,2x^2+10x+8\\ =2\left(x^2+5x+4\right)\)
\(d,x^2-5x+14\)
`->` Có đúng đề không cậu nhỉ ?
\(e,x^2-7x+10\\ =x^2-2x-5x+10\\ =x\left(x-2\right)-5\left(x-2\right)\\ =\left(x-2\right)\left(x-5\right)\)
\(g,3x^2-5x-2\\ =3x^2+x-6x-2\\ =x\left(3x+1\right)-2\left(3x+1\right)\\ =\left(3x+1\right)\left(x-2\right)\)
\(h,2x^2+x-6\\ =2x^2+4x-3x-6\\ =2x\left(x+2\right)-3\left(x+2\right)\\ =\left(x+2\right)\left(2x-3\right)\)
\(i,x^2-9x+18\\ =x^2-3x-6x+18\\ =x\left(x-3\right)-6\left(x-3\right)\\ =\left(x-3\right)\left(x-6\right)\)
\(k,2x^2-6x+9\)
`->` Cậu xem lại đề
\(e,3x^2-5x-2\\=3x^2+x-6x-2\\ =x\left(3x+1\right)-2\left(3x+1\right)\\ =\left(3x+1\right)\left(x-2\right)\)
`m,` \(x^2-5+6\)
`->` Cậu xem lại đề