K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
VN
Võ Ngọc Phương
VIP
4 tháng 9 2023
Câu 1:
\(\sqrt{16}=4\)
\(\sqrt{36}=6\)
\(\sqrt{81}=9\)
\(\sqrt{144}=12\)
\(\sqrt{625}=25\)
\(\sqrt{\dfrac{4}{9}}=\dfrac{2}{3}\)
\(\sqrt{\dfrac{36}{25}}=\dfrac{6}{5}\)
\(\sqrt{\dfrac{64}{49}}=\dfrac{8}{7}\)
\(\sqrt{\dfrac{169}{400}}=\dfrac{13}{20}\)
\(\sqrt{11\dfrac{1}{9}}=\sqrt{\dfrac{100}{9}}=\dfrac{10}{3}\)
\(\sqrt{1\dfrac{11}{25}}=\sqrt{\dfrac{36}{25}}=\dfrac{6}{5}\)
\(\sqrt{1\dfrac{13}{36}}=\sqrt{\dfrac{49}{36}}=\dfrac{7}{6}\)
Câu 2:
a) \(3.\sqrt{16}-4\sqrt{\dfrac{1}{4}}\)
\(=3.4-4.\dfrac{1}{2}\)
\(=4.\left(3-\dfrac{1}{2}\right)\)
\(=4.\dfrac{5}{2}\)
\(=10\)
b) \(-5\sqrt{\dfrac{9}{16}}+4\sqrt{0,36}-6\sqrt{0,09}\)
\(=-5.\dfrac{3}{4}+4.0,6-6.0,3\)
\(=\dfrac{-15}{4}+\dfrac{12}{5}-\dfrac{9}{5}\)
\(=\dfrac{-75+48-36}{20}=\dfrac{-63}{20}\)
c) \(2.\sqrt{9}-10.\sqrt{\dfrac{1}{25}}\)
\(=2.3-10.\dfrac{1}{5}\)
\(=6-2\)
\(=4\)
d) \(-3\sqrt{\dfrac{25}{16}}+5\sqrt{0,16}-7\sqrt{0,64}\)
\(=-3.\dfrac{5}{4}+5.0,4-7.0,8\)
\(=\dfrac{-15}{4}+2-\dfrac{28}{5}\)
\(=\dfrac{-75+40-28}{20}=\dfrac{-63}{20}\)
e) \(3\sqrt{25}-27\sqrt{\dfrac{4}{81}}\)
\(=3.5-27.\dfrac{2}{9}\)
\(=15-6\)
\(=9\)
f) \(-21\sqrt{\dfrac{100}{49}}+3\sqrt{0,04}-5\sqrt{0,25}\)
\(=-21.\dfrac{10}{7}+3.0,2-5.0,5\)
\(=-30+\dfrac{3}{5}-\dfrac{5}{2}\)
\(=\dfrac{-300+6-25}{10}=\dfrac{-319}{10}\)
h) \(5\sqrt{9}-4\sqrt{\dfrac{1}{16}}+6\sqrt{25}\)
\(=5.3-4.\dfrac{1}{4}+6.5\)
\(=15-1+30\)
\(=14+30\)
\(=44\)
g) \(10\sqrt{\dfrac{9}{25}}-14\sqrt{\dfrac{36}{49}}+24\sqrt{\dfrac{81}{64}}\)
\(=10.\dfrac{3}{5}-14.\dfrac{6}{7}+24.\dfrac{9}{8}\)
\(=6-12+27\)
\(=\left(-6\right)+27=21\)
Câu 3:
a) \(\sqrt{x}=7\)
\(=>x=49\)
b) \(\sqrt{x}=12\)
\(=>x=144\)
c) \(\sqrt{x}=15\)
\(=>x=225\)
d) \(\sqrt{x}=20\)
\(=>x=400\)
e) \(4\sqrt{x}=8\)
\(\sqrt{x}=8:4\)
\(\sqrt{x}=2\)
\(=>x=4\)
f) \(6\sqrt{x}=3\)
\(\sqrt{x}=\dfrac{3}{6}=\dfrac{1}{2}\)
\(=>x=\dfrac{1}{4}\)
g) \(\sqrt{x-1}=1\)
\(x-1=1\)
\(x=1+1\)
\(=>x=2\)
h) \(\sqrt{x+1}=2\)
\(x+1=4\)
\(x=4-1\)
\(=>x=3\)
i) \(\sqrt{x}-2=7\)
\(\sqrt{x}=7+2\)
\(\sqrt{x}=9\)
\(=>x=81\)
j) \(14-\sqrt{x}=12\)
\(\sqrt{x}=14-12\)
\(\sqrt{x}=2\)
\(=>x=4\)
k) \(12-\sqrt{x-1}=2\)
\(\sqrt{x-1}=12-2\)
\(\sqrt{x-1}=10\)
\(x-1=100\)
\(x=100+1\)
\(=>x=101\)
l) \(\sqrt{x+5}+10=20\)
\(\sqrt{x+5}=20-10\)
\(\sqrt{x+5}=10\)
\(x+5=100\)
\(x=100-5\)
\(=>x=95\)
# Wendy Dang
4 tháng 9 2023
3:
a: ĐKXĐ: x>=0
\(\sqrt{x}=7\)
=>x=7^2=49
b: ĐKXĐ: x>=0
\(\sqrt{x}=12\)
=>x=12^2=144
c: ĐKXĐ: x>=0
\(\sqrt{x}=15\)
=>x=15^2=225
d: ĐKXĐ: x>=0
\(\sqrt{x}=20\)
=>x=20^2=400
e: ĐKXĐ: x>=0
\(4\sqrt{x}=8\)
=>\(\sqrt{x}=2\)
=>x=4
f: ĐKXĐ: x>=0
\(6\cdot\sqrt{x}=3\)
=>\(\sqrt{x}=\dfrac{3}{6}=\dfrac{1}{2}\)
=>x=1/4
g: ĐKXĐ: x>=1
\(\sqrt{x-1}=1\)
=>x-1=1
=>x=2
h: ĐKXĐ: x>=-1
\(\sqrt{x+1}=2\)
=>x+1=4
=>x=3
i: ĐKXĐ: x>=0
\(\sqrt{x}-2=7\)
=>\(\sqrt{x}=9\)
=>x=81
j: ĐKXĐ: x>=0
\(14-\sqrt{x}=12\)
=>\(\sqrt{x}=14-12=2\)
=>x=4
k: ĐKXĐ: x>=1
\(12-\sqrt{x-1}=2\)
=>\(\sqrt{x-1}=10\)
=>x-1=100
=>x=101
i: ĐKXĐ: x>=-5
\(\sqrt{x+5}+10=20\)
=>\(\sqrt{x+5}=10\)
=>x+5=100
=>x=95
NN
1
21 tháng 3 2023
a: Xét ΔABE vuông tai A và ΔHBE vuông tại H có
BE chung
gócABE=gócHBE
=>ΔABE=ΔHBE
b: ΔBAE=ΔBHE
=>BA=BH; EA=EH
=>BE là trung trực của AH
29 tháng 1
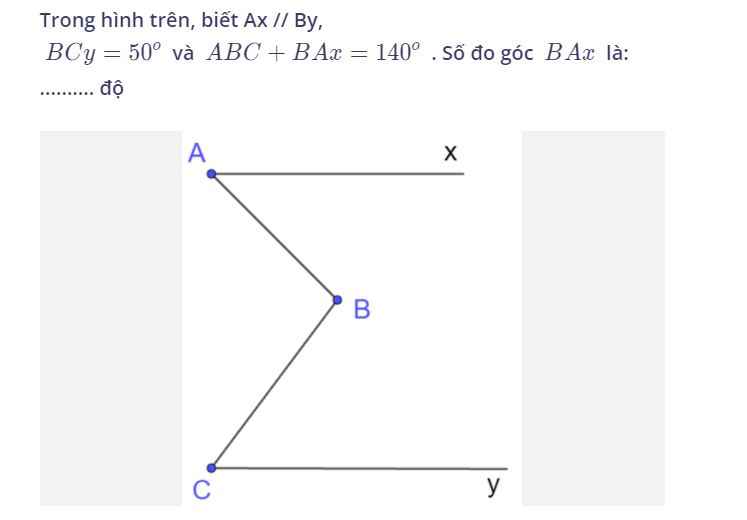
Hai tam giác này bằng nhau khi có thêm 1 trong các điều kiện sau:
AC=MN
BC=NP
\(\widehat{B}=\widehat{P}\)
\(\widehat{C}=\widehat{N}\)
KV
3 tháng 7 2023
3²ˣ⁺¹ + 2.3¹⁸ = 5.3¹⁸
3²ˣ⁺¹ = 5.3¹⁸ - 2.3¹⁸
3²ˣ⁺¹ = 3¹⁸.(5 - 2)
3²ˣ⁺¹ = 3¹⁸.3
3²ˣ⁺¹ = 3¹⁹
⇒ 2x + 1 = 19
2x = 19 - 1
2x = 18
x = 9
NB
1
29 tháng 7 2023
a: BC=căn 6^2+8^2=10cm
b: Xét ΔBAI vuông tại A và ΔBHI vuông tại H có
BI chung
góc ABI=góc HBI
=>ΔBAI=ΔBHI
=>IA=IH
mà IH<IC
nên IA<IC
c: Xét ΔIAK vuông tại A và ΔIHC vuông tại H có
IA=IH
góc AIK=góc HIC
=>ΔIAK=ΔIHC
=>AK=HC
d: Xét ΔBKC có BA/AK=BH/HC
nên AH//KC
25 tháng 6 2021
`B=M-N=3x^2+2xy-3x-7y^2-(2x+3x^2-xy+4y^3-7y^2)`
`=3x^2-3x^2+(2xy+xy)+(-3x-2x)+(-7y^2+7y^2)-4y^3`
`=3xy-5x-4y^3`
Bậc của B là `3`.
25 tháng 6 2021
Ta có: B=M-N
\(=3x^2+2xy-3x-7y^2-2x-3x^2+xy-4y^3+7y^2\)
\(=3xy-5x-4y^3\)
Bậc là 3
21 tháng 8 2021
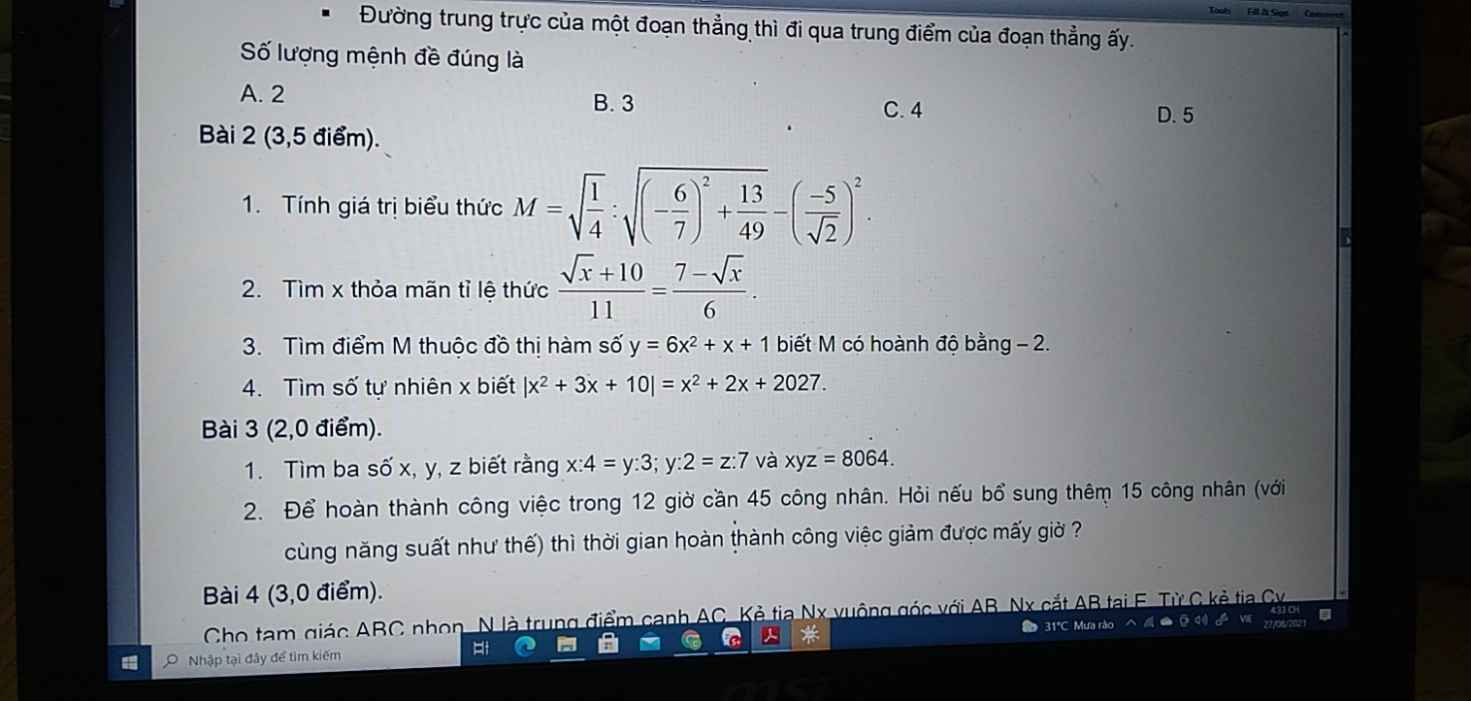
Bài 5:
a: Ta có: \(\left|\dfrac{3}{5}-x\right|\ge0\forall x\)
\(\Leftrightarrow\left|\dfrac{3}{5}-x\right|+\dfrac{1}{9}\ge\dfrac{1}{9}\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{3}{5}\)
b: Ta có: \(\left|x-\dfrac{5}{6}\right|\ge0\forall x\)
\(\Leftrightarrow-\left|x-\dfrac{5}{6}\right|\le0\forall x\)
\(\Leftrightarrow-\left|x-\dfrac{5}{6}\right|+\dfrac{2011}{2012}\le\dfrac{2011}{2012}\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{5}{6}\)
21 tháng 8 2021
Bài 4:
a: Ta có: \(\left|x-\dfrac{1}{3}\right|+4=6\)
\(\Leftrightarrow\left|x-\dfrac{1}{3}\right|=2\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{1}{3}=2\\x-\dfrac{1}{3}=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{7}{3}\\x=-\dfrac{5}{3}\end{matrix}\right.\)
b: Ta có: \(\left|5.6-x\right|=4.6\)
\(\Leftrightarrow\left[{}\begin{matrix}5.6-x=4.6\\5.6-x=-4.6\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=10.2\end{matrix}\right.\)
c: Ta có: \(\left|x\right|+x=\dfrac{2}{3}\)
\(\Leftrightarrow\left|x\right|=\dfrac{2}{3}-x\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}-x\left(x\ge0\right)\\-x=\dfrac{2}{3}-x\left(x< 0\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{2}{3}\\0x=\dfrac{2}{3}\left(loại\right)\end{matrix}\right.\Leftrightarrow x=\dfrac{1}{3}\left(nhận\right)\)
27 tháng 8 2021
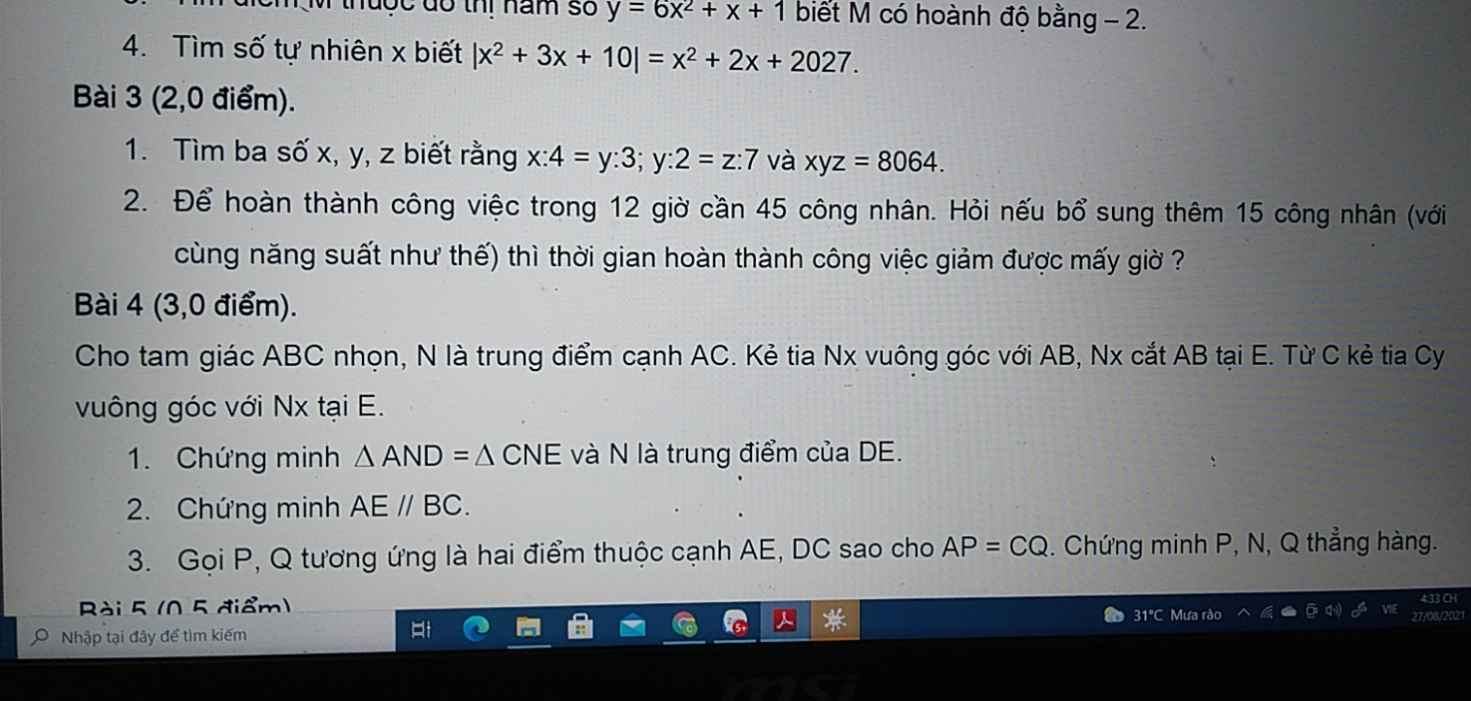
Bài 4:
a: Xét ΔAND vuông tại D và ΔCNE vuông tại E có
ND=NE
\(\widehat{AND}=\widehat{CNE}\)
Do đó: ΔAND=ΔCNE
Suy ra: ND=NE
hay N là trung điểm của DE
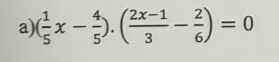
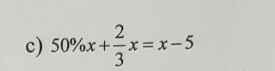
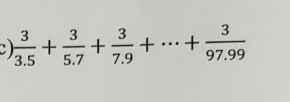
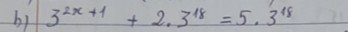
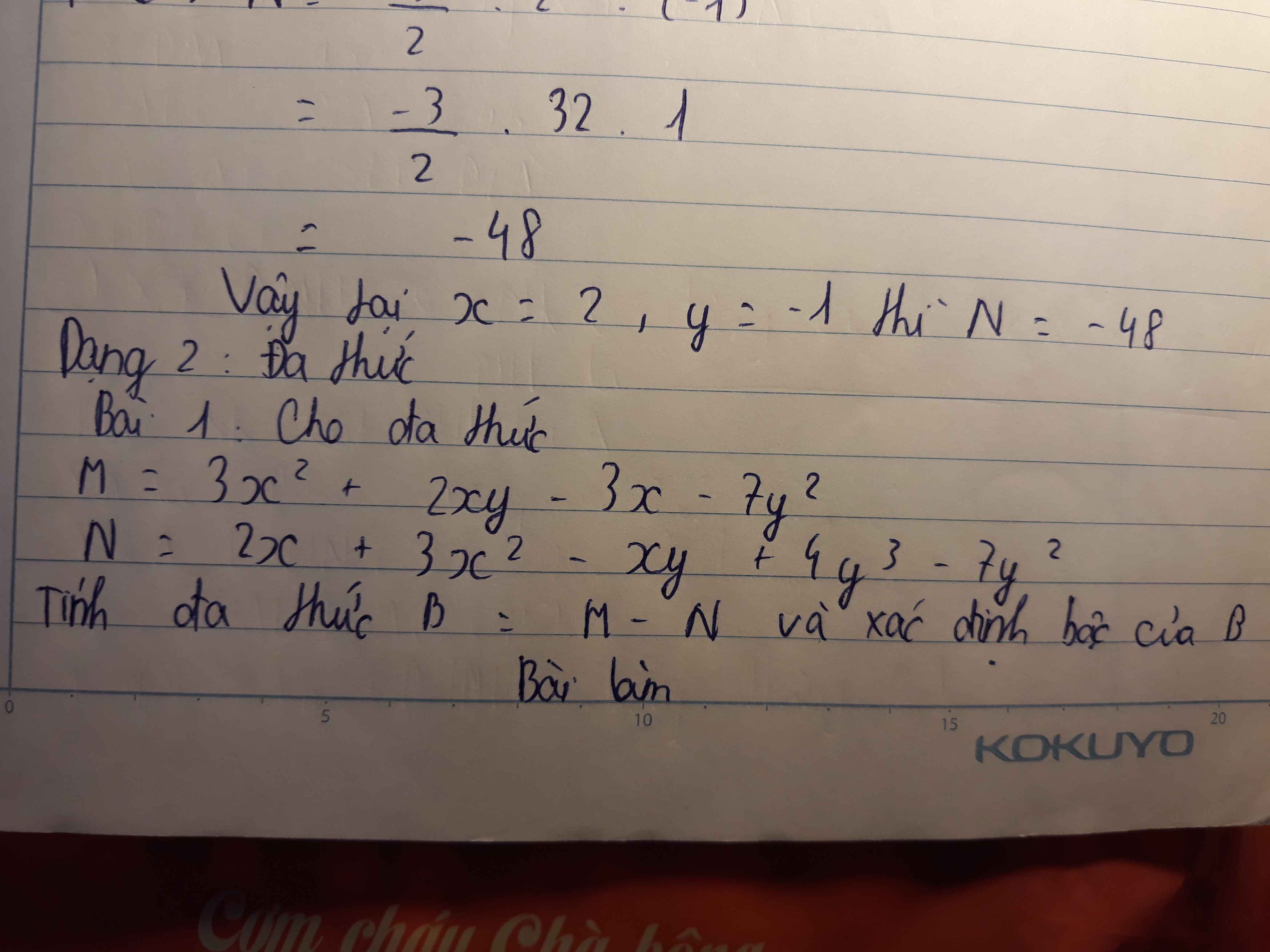
a) `(1/5x-4/5)((2x-1)/3-2/6)=0`
`[(1/5 x-4/5=0),(2/3 x -1/3 -1/3=0):}`
`[(x=4),(x=1):}`
.
c) `50% x+2/3 x=x-5`
`1/2 x+2/3 x= x-5`
`(1/2+2/3-1)x=-5`
`1/6 x=-5`
`x=-30`
.
`A=3/(3.5)+3/(5.7)+....+3/(97.99)`
`=> 2/3 A = 2/(3.5)+2/(5.7)+....+2/(97.99)`
`=1/3-1/5+1/5-1/7+...+1/97-1/99`
`=1/3-1/99`
`=32/99`
`=> A=16/33`