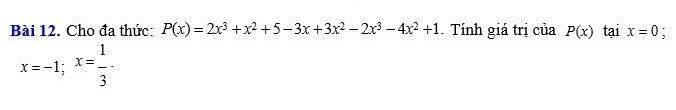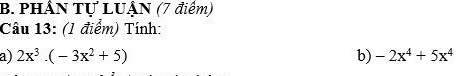Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


d. \(\dfrac{x-2}{x-1}=\dfrac{x+4}{x+7}\)
\(\Rightarrow\left(x-2\right)\left(x+7\right)=\left(x-1\right)\left(x+4\right)\)
\(\Rightarrow x^2+5x-14=x^2+3x-4\)
\(\Rightarrow x^2+5x-x^2-3x=-4+14\)
\(\Rightarrow2x=10\) \(\Rightarrow x=\dfrac{10}{3}\) \(\Rightarrow x=5\)
\(\dfrac{x-2}{x-1}=\dfrac{x+4}{x+7}\)
⇔ \(\dfrac{\left(x-2\right)\left(x+7\right)}{\left(x-1\right)\left(x+7\right)}=\dfrac{\left(x+4\right)\left(x-1\right)}{\left(x+7\right)\left(x-1\right)}\)
⇔ (x - 2)(x + 7) = (x + 4)(x - 1)
⇔ x2 + 7x - 2x - 14 = x2 - x + 4x - 4
⇔ x2 - x2 + 7x - 2x + x - 4x = 14 - 4
⇔ 2x = 10
⇔ x = 10/2 = 5

Đặt E(x)=0
\(\Leftrightarrow2x^2-3x=0\)
\(\Leftrightarrow x\left(2x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\2x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\2x=3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{3}{2}\end{matrix}\right.\)
Vậy: \(S=\left\{0;\dfrac{3}{2}\right\}\)
Đặt E(x)=0
⇔2x2−3x=0⇔2x2−3x=0
⇔x(2x−3)=0⇔x(2x−3)=0
⇔[x=02x−3=0⇔[x=02x=3⇔⎡⎣x=0x=32⇔[x=02x−3=0⇔[x=02x=3⇔[x=0x=32
Vậy: S={0;32}


a: Xét ΔDOE vuông tại O và ΔKOE vuông tại O có
EO chung
\(\widehat{DEO}=\widehat{KEO}\)
Do đó: ΔDOE=ΔKOE
b: Xét ΔEDI vàΔEKI có
ED=EK
\(\widehat{DEI}=\widehat{KEI}\)
EI chung
Do đó: ΔEDI=ΔEKI
Suy ra: \(\widehat{EDI}=\widehat{EKI}=90^0\)
hay IK\(\perp\)FE
c: Xét ΔDIQ vuông tại D và ΔKIF vuông tại K có
ID=IK
\(\widehat{DIQ}=\widehat{KIF}\)
Do đó: ΔDIQ=ΔKIF
Suy ra: IQ=IF

\(2\left(x-3\right)^4-3^2=503\\ \Rightarrow2\left(x-3\right)^4=512\\ \Rightarrow\left(x-3\right)^4=256\\ \Rightarrow\left[{}\begin{matrix}x-3=4\\x-3=-4\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=7\\x=-1\end{matrix}\right.\)

Ta có: \(20^x:14^x=\dfrac{10}{7}x\)
\(\Leftrightarrow\left(\dfrac{10}{7}\right)^x=\dfrac{10}{7}x\)
\(\Leftrightarrow x=\left(\dfrac{10}{7}\right)^{x-1}\)
Đến đây mình bí rồi, xin lỗi bạn!

a: Xét ΔOAM vuông tại A và ΔOBM vuông tại B có
OM chung
\(\widehat{AOM}=\widehat{BOM}\)
Do đó: ΔOAM=ΔOBM
b: Xét ΔOEF có
OM là đường cao
OM là đường phân giác
Do đó: ΔOEF cân tại O
mà OM là đường cao
nên M là trung điểm của FE
hay FM=EM

`P(x)=2x^3+x^2+5-3x+3x^2-2x^3-4x^2+1`
`= (2x^3-2x^3)+(x^2+3x^2-4x^2)-3x+(5+1)`
`= -3x+6`
Thay `x=0`
`P(0)=-3*0+6=6`
Thay `x=-1`
`P(-1)=(-3)*(-1)+6=3+6=9`
Thay `x=1/3`
`P(1/3)=(-3)*1/3+6=-1+6=5`

\(a,2x^3.\left(-3x^2+5\right)=2x^3.\left(-3x^2\right)+2x^3.5=-6x^{3+2}+10x^3\\ =-6x^5+10x^3\\ b,-2x^4+5x^4=\left(-2+5\right)x^4=3x^4\)

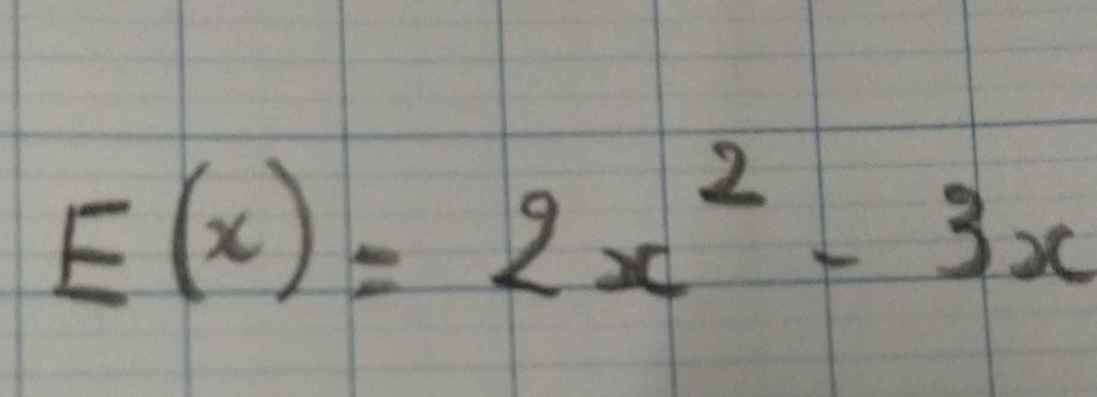

 Giúp mình với aa (Giải chi tiết + nếu được thì thêm lời giải thích ở cuối bài làm giúp mình nha
Giúp mình với aa (Giải chi tiết + nếu được thì thêm lời giải thích ở cuối bài làm giúp mình nha