K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TD
14
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 6 2021
Tất cả k dưới đây đều là \(k\in Z\)
6.
\(\Leftrightarrow\sqrt{3}cot\left(3x-\dfrac{\pi}{3}\right)=1\)
\(\Leftrightarrow cot\left(3x-\dfrac{\pi}{3}\right)=\dfrac{1}{\sqrt{3}}\)
\(\Leftrightarrow cot\left(3x-\dfrac{\pi}{3}\right)=cot\left(\dfrac{\pi}{3}\right)\)
\(\Leftrightarrow3x-\dfrac{\pi}{3}=\dfrac{\pi}{3}+k\pi\)
\(\Leftrightarrow3x=\dfrac{2\pi}{3}+k\pi\)
\(\Leftrightarrow x=\dfrac{2\pi}{9}+\dfrac{k\pi}{3}\)
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 6 2021
7.
\(\Leftrightarrow\sqrt{3}tan\left(3x-15^0\right)=-1\)
\(\Leftrightarrow tan\left(3x-15^0\right)=-\dfrac{1}{\sqrt{3}}\)
\(\Leftrightarrow tan\left(3x-15^0\right)=tan\left(-30^0\right)\)
\(\Leftrightarrow3x-15^0=-30^0+k180^0\)
\(\Leftrightarrow3x=-15^0+k180^0\)
\(\Leftrightarrow x=-3^0+k60^0\)
PN
0
HP
6 tháng 9 2021
1.
ĐK: \(\left\{{}\begin{matrix}\dfrac{1+sinx}{1-sinx}\ge0\\1-sinx\ne0\end{matrix}\right.\Leftrightarrow1-sinx\ne0\Leftrightarrow sinx\ne1\Leftrightarrow x=\dfrac{\pi}{2}+k2\pi\)
TA
31 tháng 7 2021
`\lim (\sqrt(4n+3) -\sqrt(n+1))`
`=\lim \sqrtn (\sqrt(4+3/n)-\sqrt(1+1/n))`
`=+oo`
Vì `{(\limn=+oo),(\lim(\sqrt(4+3/n)-\sqrt(1+1/n))=1>0):}`
C
1
8 tháng 10 2023
a: \(=\dfrac{-\dfrac{1}{2}\left[cos\left(a+b+a-b\right)-cos\left(a+b-a+b\right)\right]}{cos^2b-cos^2a}\)
\(=\dfrac{-\dfrac{1}{2}\cdot\left[cos2a-cos2b\right]}{\dfrac{1-cos2b}{2}-\dfrac{1-cos2a}{2}}\)
\(=\dfrac{-\dfrac{1}{2}\cdot\left(cos2a-cos2b\right)}{\dfrac{1-cos2b-1+cos2a}{2}}=\dfrac{-\dfrac{1}{2}\cdot\left(cos2a-cos2b\right)}{\dfrac{1}{2}\cdot\left(cos2a-cos2b\right)}=-1\)
c: \(T=\dfrac{sina+sinb\cdot\left(cosa\cdot cosb-sina\cdot sinb\right)}{cosa-sinb\cdot\left(sina\cdot cosb+sinb\cdot cosa\right)}-tan\left(a+b\right)\)
\(=\dfrac{sina+sinb\cdot cosa\cdot cosb-sin^2b\cdot sina}{cosa-sinb\cdot sina\cdot cosb-sin^2b\cdot cosa}-tan\left(a+b\right)\)
\(=\dfrac{sina\left(1-sin^2b\right)+sinb\cdot cosa\cdot cosb}{cosa\left(1-sin^2b\right)-sinb\cdot sina\cdot cosb}\)-tan(a+b)
\(=\dfrac{sina\cdot cos^2b+sinb\cdot cosa\cdot cosb}{cosa\cdot cos^2b-sinb\cdot sina\cdot cosb}-tan\left(a+b\right)\)
\(=\dfrac{sina\cdot cosb+sinb\cdot cosa}{cosa\cdot cosb-sina\cdot sinb}-tan\left(a+b\right)\)
\(=\dfrac{sin\left(a+b\right)}{cos\left(a+b\right)}-tan\left(a+b\right)=0\)
HN
26 tháng 10 2021
cos x = cos\(\dfrac{\pi}{6}\)
x = \(\dfrac{\pi}{6}\) + k2\(\pi\) (1)
x = - \(\dfrac{\pi}{6}\) + k2\(\pi\) (2)
(1) thế k = -1 -> x = \(\dfrac{-11\pi}{6}\) (loại) *k= -2, k =-3,... loại luôn*
thế k = 0 -> x = \(\dfrac{\pi}{6}\) (nhận)
thế k = 1 -> x = \(\dfrac{13\pi}{6}\) (loại) *k=2, k=3,... loại luôn*
vậy (1) có 1 nghiệm
(2) thế k = - 1 -> x = \(\dfrac{-13\pi}{6}\) ( loại)
thế k = 0 -> x = \(\dfrac{-\pi}{6}\) (nhận)
thế k = 1 -> x = \(\dfrac{11\pi}{6}\) ( loại)
vậy tổng nghiệm (1) + (2) là 2 -> Đáp án câu D
#Chúc em học tốt
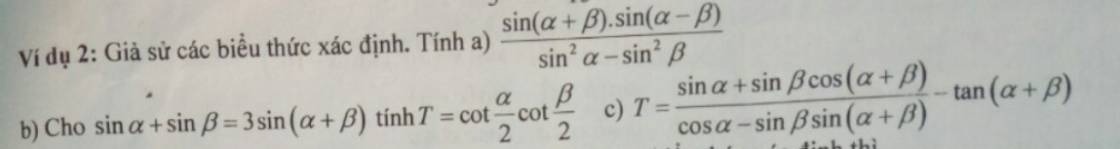
B