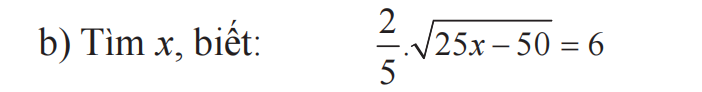Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 6: Để hàm số y=(1-m)x+3 nghịch biến trên R thì 1-m<0
=>m>1
=>Chọn B
Câu 7: D
Câu 10: (D)//(D')
=>\(\left\{{}\begin{matrix}3m+1=2\left(m+1\right)\\-2\ne-2\left(loại\right)\end{matrix}\right.\Leftrightarrow m\in\varnothing\)
=>Chọn D
Câu 11: \(x^2+2x+2=\left(x+1\right)^2+1>=1>0\forall x\)
=>\(\sqrt{x^2+2x+2}\) luôn xác định với mọi số thực x
=>Chọn A
Câu 12: Để hai đường thẳng y=x+3m+2 và y=3x+2m+3 cắt nhau tại một điểm trên trục tung thì \(\left\{{}\begin{matrix}1\ne3\left(đúng\right)\\3m+2=2m+3\end{matrix}\right.\)
=>3m+2=2m+3
=>m=1
=>Chọn C

DKXD: \(x\ge2\)
\(\Leftrightarrow\dfrac{2}{5}.5\sqrt{x-2}=6\\ \Leftrightarrow\sqrt{x-2}=6\\ \Leftrightarrow x-2=36\\ \Leftrightarrow x=38\)
\(\dfrac{2}{5}\sqrt{25x-50}=6\)
⇔ \(\sqrt{25x-50}=15\)
⇔ \(25x-50=225\)
⇔ \(25x=275\)
⇔ \(x=11\)

10D.
Hai đường thẳng (D) và (D') cùng đi qua điểm (0;-2) nên chúng không bao giờ song song nhau
11.A
\(x^2+2x+2=\left(x+1\right)^2+1>0;\forall x\in R\)
12.C
Hai đồ thị cắt nhau tại 1 điểm trên trục tung khi:
\(3m+2=3+2m\Rightarrow m=1\)
10D.
Hai đường thẳng (D) và (D') cùng đi qua điểm (0;-2) nên chúng không bao giờ song song nhau
11.A
x2+2x+2=(x+1)2+1>0;∀x∈Rx2+2x+2=(x+1)2+1>0;∀x∈R
12.C
Hai đồ thị cắt nhau tại 1 điểm trên trục tung khi:
3m+2=3+2m⇒m=1



a: Kẻ OH vuông góc BC
=>OH là khoảng cách từ O đến BC
ΔOBC cân tại O
mà OH là đường cao
nên H là trung điểm của BC
=>\(HB=HC=\dfrac{BC}{2}=\dfrac{R\sqrt{3}}{2}\)
ΔOHB vuông tại H
=>\(OH^2+HB^2=OB^2\)
=>\(OH^2=OB^2-HB^2=R^2-\left(\dfrac{R\sqrt{3}}{2}\right)^2=\dfrac{R^2}{4}\)
=>OH=R/2
=>d(O;BC)=R/2
b: Xét ΔOBC có \(cosBOC=\dfrac{OB^2+OC^2-BC^2}{2\cdot OB\cdot OC}\)
=>\(cosBOC=\dfrac{R^2+R^2-3R^2}{2\cdot R\cdot R}=\dfrac{-1}{2}\)
=>\(\widehat{BOC}=120^0\)
ΔOBC cân tại O
=>\(\widehat{OBC}=\widehat{OCB}=\dfrac{180^0-120^0}{2}=30^0\)

\(\hept{\begin{cases}|x-2|+2|y-1|=9\\x+|y-1|=-1\end{cases}}\)<=> \(\hept{\begin{cases}\left(x-2\right)+2\left(y-1\right)=9\\x+\left(y-1\right)=-1\end{cases}}\)
<=> \(\hept{\begin{cases}x-2+2y-2=9\\x+y-1=-1\end{cases}}\)<=>\(\hept{\begin{cases}x+2y=13\\x+y=0\end{cases}}\)<=> \(\hept{\begin{cases}x=-13\\y=13\end{cases}}\)

\(\frac{a\sqrt{a}+b\sqrt{b}}{\sqrt{a}+\sqrt{b}}=\frac{\left(\sqrt{a}+\sqrt{b}\right)\left(a+\sqrt{ab}+b\right)}{\sqrt{a}+\sqrt{b}}=a+\sqrt{ab}+b\)

1:
a: =12/10-7/10=5/10=1/2
b: \(=\dfrac{4}{13}-\dfrac{4}{13}+\dfrac{-5}{11}-\dfrac{6}{11}=-\dfrac{11}{11}=-1\)
2:
a: x+2/7=-11/7
=>x=-11/7-2/7=-13/7
b: (x+3)/4=-7/2
=>x+3=-14
=>x=-17