K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
2D
Mn giải giúp mình với mình cần gấp lắm hôm nay mình pgair nộp rồi
3
14 tháng 10 2021
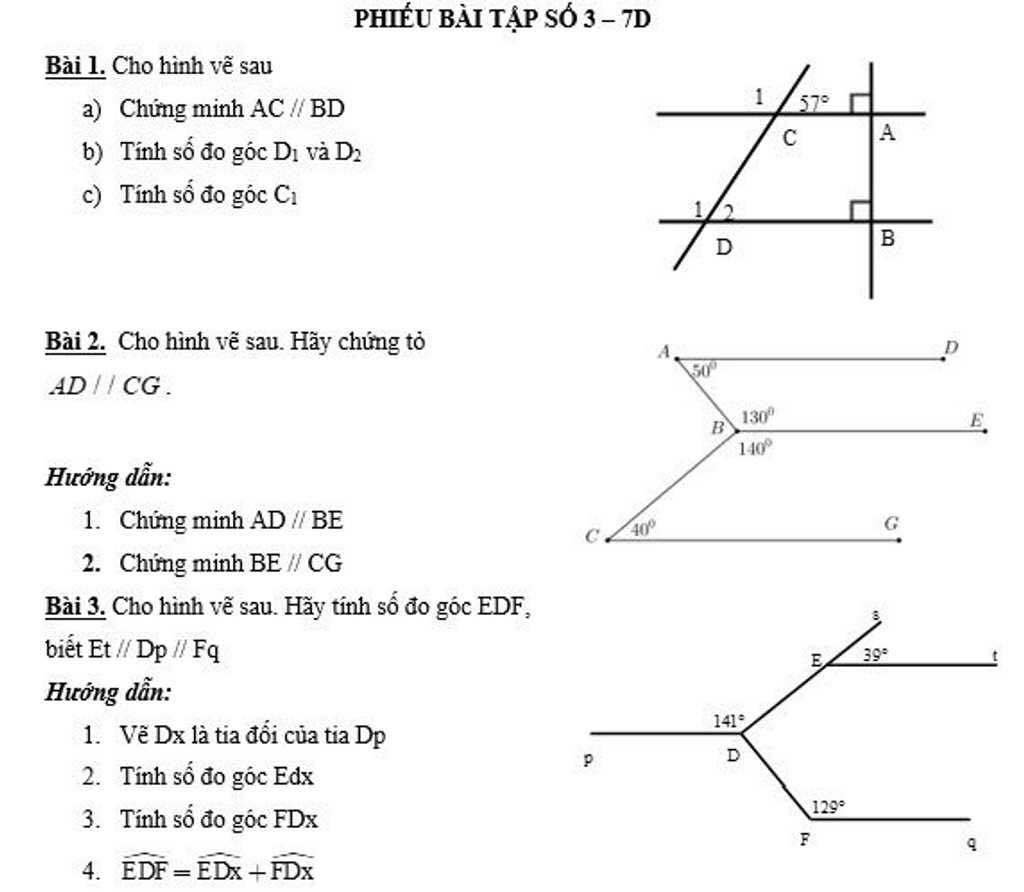
\(1,\\ a,\left\{{}\begin{matrix}AC\perp AB\\BD\perp AB\end{matrix}\right.\Rightarrow AC//BD\\ b,AC//BD\Rightarrow\widehat{D_2}=\widehat{C_1}=57^0\left(đồng.vị\right)\\ \widehat{D_2}+\widehat{D_1}=180^0\left(kề.bù\right)\Rightarrow\widehat{D_1}=180^0-57^0=123^0\\ c,AC//BD\Rightarrow\widehat{D_1}=\widehat{C_1}=123^0\left(đồng.vị\right)\)
14 tháng 10 2021
\(2,\\ \widehat{DAB}+\widehat{ABE}=50^0+130^0=180^0\)
Mà 2 góc này ở vị trí TCP nên AD//BE (1)
\(\widehat{EBC}+\widehat{BCG}=140^0+40^0=180^0\)
Mà 2 góc này ở vị trí TCP nên BE//CG (2)
Từ (1)(2) ta được AD//CG
DC
0
LN
27 tháng 2 2018
Ta có: \(\frac{x-y}{3}=\frac{x+y}{13}=\frac{x-y+x+y}{16}=\frac{2x}{16}=\frac{x}{8}=\frac{25x}{200}=\frac{xy}{200}\)
Suy ra: \(25x=xy\Rightarrow y=25\)
Ta có: \(\frac{x-y}{3}=\frac{x+y}{13}\)
Suy ra: \(13x-13y=3x+3y\)
Thế y vào đẳng thức trên:
\(13x-325=3x+75\)
Suy ra: \(10x=325+75=400\Rightarrow x=40\)
Vậy ........
mn giúp mình trong hôm nay nha
LL
0
LT
2
30 tháng 9 2021
a) Có : AB ⊥ AC tại A ( gt )
CD ⊥ AC tại C ( gt )
=> AB//CD ( Quan hệ từ vuông góc đến song song )
b) Kéo dài CD ( như hình vẽ ).
Có : Góc ACB + Góc C1 = 180o ( Tính chất 2 góc kề bù )
90o + Góc C1 = 180o ( Thay số )
Góc C1 = 90o
Có : Góc C1 + Góc C2 = Góc ACE ( Tính chất cộng góc )
90o + Góc C2 = 140o ( Thay số )
90o + Góc C2 = 50o
Có : Góc C2 + Góc CEF = 50o + 130o = 180o
Mà 2 góc này nằm ở vị trí phía trong cùng.
=> CD//EF ( dhnb )
SM
20 tháng 3 2018
Xét tam giác ABC có A = 180 - C - B =180 - 120 - 30 = 30
Vì AE là phân giác góc ngoài tại A
=> BAE = ( 180 - A ) / 2 = ( 180 - 30 ) / 2 = 75
Có ABE + ABC = 180
=> ABE = 180 - ABC = 180 - 120 = 60
Xét tam giác AEB có BEA + BAE + ABE = 180
=> AEB = 180 - 60 -75 = 45
Vậy AEB = 45
DC
0
Ta có : \(a-2b=1\)
⇒ \(a=1+2b\)
Thay \(a=1+2b\) vào biểu thức A. Ta được:
\(A=\dfrac{1+2b+b}{3b+1}+\dfrac{3b+1+2b+1}{2\left(1+2b\right)+b}\)
⇔ \(A=\dfrac{3b+1}{3b+1}+\dfrac{5b+2}{5b+2}\)
⇔ \(A=1+1\)
⇔ \(A=2\)
\(VậyA=2\)