VT
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TH
1
16 tháng 6 2023
2:
1+cot^2a=1/sin^2a
=>1/sin^2a=1681/81
=>sin^2a=81/1681
=>sin a=9/41
=>cosa=40/41
tan a=1:40/9=9/40
Mọi người giúp mình với, giải chi tiết (+giải thích giúp mình nha), cảm ơn mọi người rất nhiều lun =)
AH
Akai Haruma
Giáo viên
12 tháng 7 2023
Bạn nên chịu khó gõ đề ra khả năng được giúp sẽ cao hơn.
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
13 tháng 7 2023
Câu h của em đây nhé
h, ( 1 + \(\dfrac{3-\sqrt{3}}{\sqrt{3}-1}\)).(1 - \(\dfrac{3+\sqrt{3}}{\sqrt{3}+1}\))
= \(\dfrac{\sqrt{3}-1+3-\sqrt{3}}{\sqrt{3}-1}\).\(\dfrac{\sqrt{3}+1-3-\sqrt{3}}{\sqrt{3}+1}\)
= \(\dfrac{2}{\sqrt{3}-1}\).\(\dfrac{-2}{\sqrt{3}+1}\)
= \(\dfrac{-4}{2}\)
= -2
Các bạn ơi giúp mk với. Mk cần gấp lắm ạ.Các bạn giải chi tiết giúp mk nhé . Mk hứa sẽ vote 5* cho . Mk cảm ơn nhiều.
6 tháng 8 2021
a, \(2\sqrt{3}-\sqrt{4+x^2}=0\Leftrightarrow\sqrt{4+x^2}=2\sqrt{3}\)
\(\Leftrightarrow x^2+4=12\Leftrightarrow x^2=8\Leftrightarrow x=\pm2\sqrt{2}\)
b, \(\sqrt{16x+16}-\sqrt{9x+9}=0\)ĐK : x >= -1
\(\Leftrightarrow4\sqrt{x+1}-3\sqrt{x+1}=0\Leftrightarrow\sqrt{x+1}=0\Leftrightarrow x+1=0\Leftrightarrow x=-1\)
c, \(\sqrt{4\left(x+2\right)^2}=8\Leftrightarrow2\left|x+2\right|=8\Leftrightarrow\left|x+2\right|=4\)
TH1 : \(x+2=4\Leftrightarrow x=2\)
TH2 : \(x+2=-4\Leftrightarrow x=-6\)
6 tháng 8 2021
c: Ta có: \(\sqrt{4\left(x+2\right)^2}=8\)
\(\Leftrightarrow\left|x+2\right|=4\)
\(\Leftrightarrow\left[{}\begin{matrix}x+2=4\\x+2=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-6\end{matrix}\right.\)
VT
0
92
1
11 tháng 7 2023
a: Khi m=2 thì (1) sẽ là:
2x+y=2 và 4x+3y=10
=>x=-2 và y=6
b: 2x+y=m và 4x+3y=10
=>4x+2y=2m và 4x+3y=10
=>4x+3y=10 và 4x+2y=2m
=>y=10-2m và 2x=m-10+2m=3m-10
=>y=10-2m và x=3/2m-5
x>0 và y>0
=>10-2m>0 và 3/2m-5>0
=>m>5:3/2=10/3 và m<5
=>10/3<m<5
13 tháng 2 2022
a,\(\Delta=3^2-4\left(-2\right).6=9+48=57\)
\(x_1=\dfrac{-3+\sqrt{57}}{-4}=\dfrac{3-\sqrt{57}}{4}\)
\(x_2=\dfrac{-3-\sqrt{57}}{-4}=\dfrac{3+\sqrt{57}}{4}\)
b, \(\Delta=6^2-4.3.3=36-36=0\)
\(\Rightarrow x_1=x_2=\dfrac{-6}{2.3}=\dfrac{-6}{6}=-1\)
c, \(\Delta=1^2-4.6.5=1-120=-119< 0\)
Vậy pt vô nghiệm
LN
19 tháng 7 2021
\(\dfrac{1}{2+\sqrt{3}}+\dfrac{1}{2-\sqrt{3}}\\ =\dfrac{2-\sqrt{3}}{\left(2+\sqrt{3}\right)\left(2-\sqrt{3}\right)}+\dfrac{2+\sqrt{3}}{\left(2+\sqrt{3}\right)\left(2-\sqrt{3}\right)}\\ =\dfrac{2-\sqrt{3}+2+\sqrt{3}}{2^2-\left(\sqrt{3}\right)^2}\\ =\dfrac{2+2}{4-3}\\ =4\)
19 tháng 7 2021
Ta có: \(\dfrac{1}{2+\sqrt{3}}+\dfrac{1}{2-\sqrt{3}}\)
\(=2-\sqrt{3}+2+\sqrt{3}\)
=4
NC
2
9 tháng 11 2021
1, Áp dụng PTG: \(AC=\sqrt{BC^2-AB^2}=8\left(cm\right)\)
Áp dụng HTL: \(\left\{{}\begin{matrix}CH=\dfrac{AC^2}{BC}=6,4\left(cm\right)\\AH=\dfrac{AB\cdot AC}{BC}=4,8\left(cm\right)\end{matrix}\right.\)
\(\sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{4}{5}\approx\sin53^0\\ \Rightarrow\widehat{B}\approx53^0\\ \Rightarrow\widehat{C}\approx90^0-53^0=37^0\)
2,
a, Áp dụng HTL: \(\left\{{}\begin{matrix}AD\cdot AB=AH^2\\AE\cdot AC=AH^2\end{matrix}\right.\Rightarrow AD\cdot AB=AE\cdot AC\)
b, \(AD\cdot AB=AE\cdot AC\Rightarrow\dfrac{AD}{AC}=\dfrac{AE}{AB}\Rightarrow\Delta ABC\sim\Delta AED\left(c.g.c\right)\)
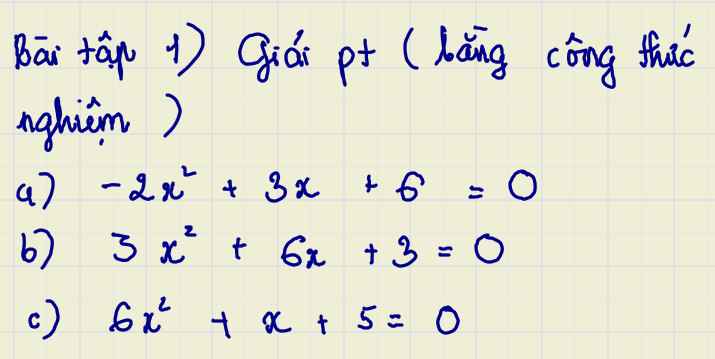
bạn đánh dâu cho mik nha
góc nào vuông vậy bạn:))