K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
KY
4
T
1
TM
18 tháng 1 2022
a. \(\left(x-5\right)^2+3\left(x-5\right)=0\)
\(\Leftrightarrow\left(x-5\right)\left(x-5+3\right)=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-5=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=5\\x=2\end{matrix}\right.\)
Vậy: Phương trình có tập nghiệm \(S=\left\{5;2\right\}\)
b. \(\dfrac{2x-1}{3}-\dfrac{5x+2}{7}=x+13\)
\(\Leftrightarrow\dfrac{7\left(2x-1\right)-3\left(5x+2\right)}{21}=\dfrac{21\left(x+13\right)}{21}\)
\(\Leftrightarrow7\left(2x-1\right)-3\left(5x+2\right)=21\left(x+13\right)\)
\(\Leftrightarrow14x-7-15x-6=21x+273\)
\(\Leftrightarrow-22x=286\)
\(\Leftrightarrow x=-13\)
Vậy: Phương trình có tập nghiệm \(S=\left\{-13\right\}\)
c. \(\dfrac{5\left(1-2x\right)}{3}+\dfrac{x}{2}=\dfrac{3\left(x-5\right)}{4}-2\)
\(\Leftrightarrow\dfrac{20\left(1-2x\right)+6x}{12}=\dfrac{9\left(x-5\right)-24}{12}\)
\(\Leftrightarrow20\left(1-2x\right)+6x=9\left(x-5\right)-24\)
\(\Leftrightarrow2x-40x+6x=9x-45-24\)
\(\Leftrightarrow-41x=-69\)
\(\Leftrightarrow x=\dfrac{69}{41}\)
Vậy: Phương trình có tập nghiệm \(S=\left\{\dfrac{69}{41}\right\}\)
1 tháng 10 2021
(3x-4-x-1)(3x-4+x+1)=0
(2x-5)(4x-3)=0
2x-5 = 0 hoặc 4x-3=0
2x=5 hoặc 4x=3
x=5/2 hoặc x=3/4
24 tháng 10 2021
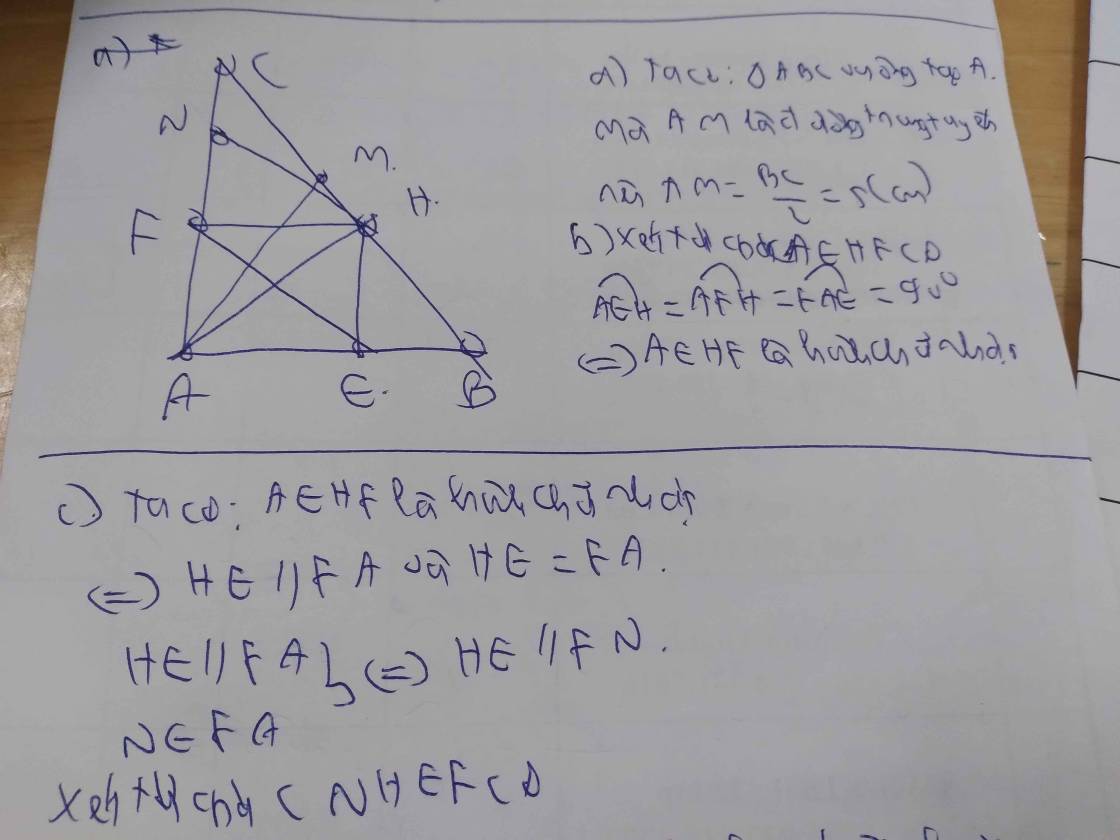
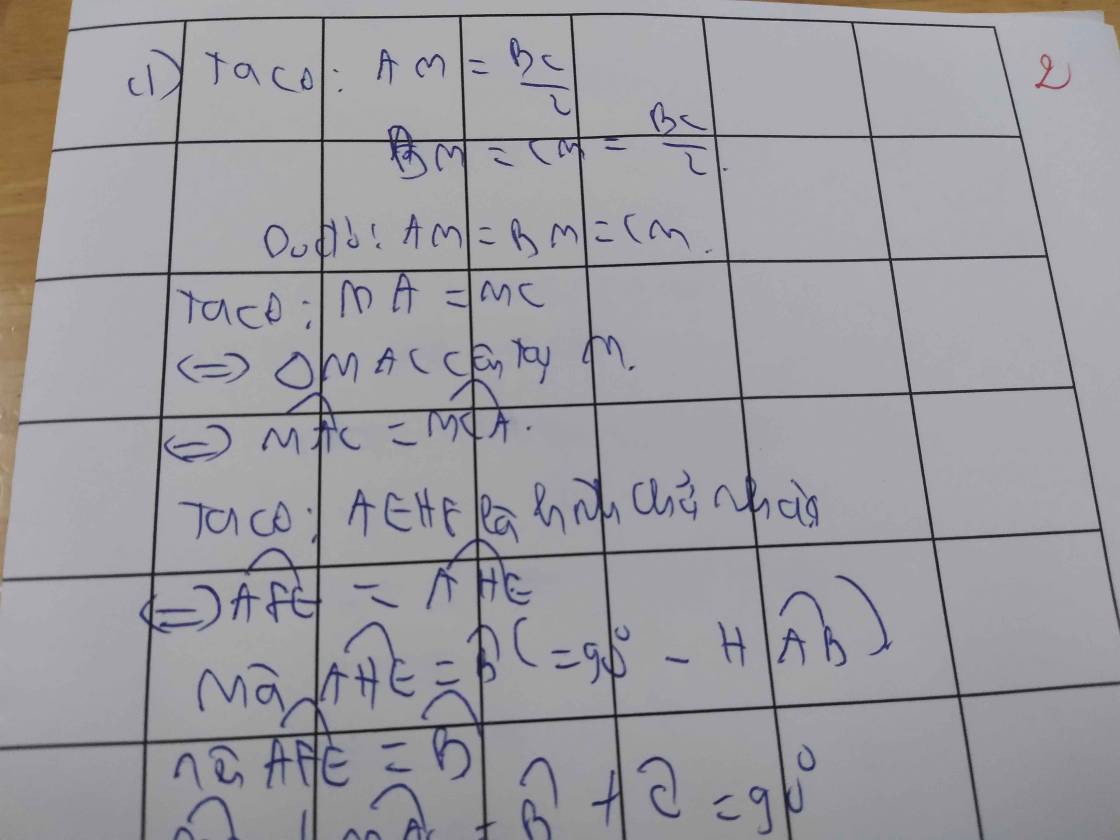
b: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{EAF}=90^0\)
Do đó: AEHF là hình chữ nhật
Suy ra: AH=EF
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
26 tháng 8 2023
a, - \(\dfrac{1}{3}\).\(xy\).(3\(x^3\).y2 - 6\(x^2\) + y2)
= - \(x^4\).y3 + 2\(x^3\).y - \(\dfrac{1}{3}\).\(xy^3\)
b, (2\(x\) -3).(4\(x\)2 + 6\(x\) + 9)
= (2\(x\))3 - 33
= 8\(x^3\) - 27
21 tháng 10 2021
Bài 6:
a) \(x^2-2x+4=\left(x^2-2x+1\right)+3=\left(x-1\right)^2+3>0\forall x\)
b) \(-x^2+4x-5=-\left(x^2-4x+4\right)-1=-\left(x-2\right)^2-1< 0\forall x\)
c) \(\left(x-2\right)\left(x-4\right)+3=x^2-6x+11=\left(x^2-6x+9\right)+2=\left(x-3\right)^2+2>0\forall x\)
d) \(-2x^2+5x-19=\dfrac{-4x^2+10x-38}{2}=\dfrac{-\left(4x^2-10x+6,25\right)-31,75}{2}=\dfrac{-\left(2x-2,5\right)^2-31,75}{2}< 0\forall x\)
21 tháng 10 2021
Câu 5:
\(a^3+b^3=3ab-1\\ \Leftrightarrow\left(a+b\right)^3-3ab\left(a+b\right)-3ab+1=0\\ \Leftrightarrow\left(a+b+1\right)\left(a^2+2ab+b^2-a-b+1\right)-3ab\left(a+b+1\right)=0\\ \Leftrightarrow\left(a+b+1\right)\left(a^2+b^2+1-ab-a-b\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}a+b+1=0\left(vô.lí.do.a,b>0\right)\\a^2+b^2+1-ab-a-b=0\left(1\right)\end{matrix}\right.\\ \left(1\right)\Leftrightarrow2a^2+2b^2+2-2ab-2a-2b=0\\ \Leftrightarrow\left(a-b\right)^2+\left(a-1\right)^2+\left(b-1\right)^2=0\\ \Leftrightarrow\left\{{}\begin{matrix}a-b=0\\a-1=0\\b-1=0\end{matrix}\right.\Leftrightarrow a=b=1\)
Vậy \(T=\left(1-2\right)^{2020}+\left(1-1\right)^{2021}=\left(-1\right)^{2020}+0=1\)
28 tháng 1 2023
a: Xét tứ giác MBQC có
N la trung điểm chung của MQ và BC
=>MBQC là hình bình hành
b: Xet tứ giácc AMQC có
AM//QC
AM=QC
góc MAC=90 độ
=>AMQC là hình chữ nhật
c: Xét ΔBAC có
N là trung điểm của CB
NK//AB
=>K là trung điểm của AC
Xét ΔCAB có
AN,BK,CM là các trung tuyến
nên ba đường này sẽ đồng quy
=>B,H,K thẳng hàng
MC
4
15 tháng 1 2022
Bài 2:
a: =>168x+20=6x-21
=>162x=-41
hay x=-41/162
b: \(\Leftrightarrow2\left(3x-8\right)=3\left(5-x\right)\)
=>6x-16=15-3x
=>9x=31
hay x=31/9
c: \(\Leftrightarrow4\left(x^2+8x-20\right)-\left(x+4\right)\left(x+10\right)=3\left(x^2+2x-8\right)\)
\(\Leftrightarrow4x^2+32x-80-x^2-14x-40-3x^2-6x+24=0\)
=>12x-96=0
hay x=8
câu trả lời bằng hình