HM
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LN
1
HT
24 tháng 12 2016
\(y'=\left(2m+1\right)\cos x+3-m\)
Hàm số đã cho đồng biến trên R \(\Leftrightarrow y'\ge0,\forall x\in R\)
\(\Leftrightarrow\left(2m+1\right)\cos x\le m-3\) (1)
*TH: \(2m+1< 0\Leftrightarrow m< \frac{-1}{2}\), ta có
\(\left(1\right)\Leftrightarrow\cos x\ge\frac{m-3}{2m+1}\) (không thoả với mọi x)
*TH: \(2m+1>0\Leftrightarrow m>\frac{-1}{2}\), ta có
\(\left(1\right)\Leftrightarrow\cos x\le\frac{m-3}{2m+1}\) (2)
(2) đúng với mọi x khi và chỉ khi \(\left|\frac{m-3}{2m+1}\right|>1\Leftrightarrow\left[\begin{array}{nghiempt}m< -4\\m>\frac{2}{3}\end{array}\right.\)
kết hợp \(m>\frac{-1}{2}\) ta có m > 3/2 là giá trị cần tìm
HT
10 tháng 4 2021
31/
\(3z^2-2z+27=0\)
\(\Delta'=\left(-1\right)^2-3.27=1-3.27=-80\)
\(\Delta'\) có 2 căn bậc 2 là \(\pm4i\sqrt{5}\)
\(\Rightarrow\left\{{}\begin{matrix}z_1=\dfrac{1+4i\sqrt{5}}{3}\\z_2=\dfrac{1-4i\sqrt{5}}{3}\end{matrix}\right.\Rightarrow\left|z_1\right|=\left|z_2\right|=\sqrt{\left(\dfrac{1}{3}\right)^2+\left(\dfrac{4\sqrt{5}}{3}\right)^2}=3\)
\(\Rightarrow z_1\left|z_2\right|+z_2\left|z_1\right|=1+4i\sqrt{5}+1-4i\sqrt{5}=2\) => A
32/ \(\Delta'=4-29=-25\Rightarrow\left\{{}\begin{matrix}z_1=-2+5i\\z_2=-2-5i\end{matrix}\right.\Rightarrow\left|z_1\right|=\left|z_2\right|=\sqrt{2^2+5^2}=\sqrt{29}\)
\(\Rightarrow\left|z_1\right|^4+\left|z_2\right|^4=2.\sqrt{29^4}=1682\) => B
33/ \(\Delta=1-12=-11\Rightarrow\left\{{}\begin{matrix}z_1=\dfrac{1+i\sqrt{11}}{6}\\z_2=\dfrac{1-i\sqrt{11}}{6}\end{matrix}\right.\Rightarrow\left|z_1\right|=\left|z_2\right|=\sqrt{\left(\dfrac{1}{6}\right)^2+\left(\dfrac{\sqrt{11}}{6}\right)^2}=\dfrac{\sqrt{3}}{3}\)
\(\Rightarrow\left|z_1\right|+\left|z_2\right|=\dfrac{2\sqrt{3}}{3}\) => D
34/ \(\Delta=1-4.3.2=-23\Rightarrow\left\{{}\begin{matrix}z_1=\dfrac{1-i\sqrt{23}}{6}\\z_2=\dfrac{1+i\sqrt{23}}{6}\end{matrix}\right.\Rightarrow\left|z_1\right|=\left|z_2\right|=\sqrt{\dfrac{1}{36}+\dfrac{23}{36}}=\dfrac{\sqrt{6}}{3}\)
\(\Rightarrow T=2.\left(\dfrac{\sqrt{6}}{3}\right)^2=\dfrac{4}{3}\) => C
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 4 2021
Xét \(I_1=2\int\limits^{\dfrac{\pi}{2}}_0f\left(sinx\right)cosxdx=2\int\limits^{\dfrac{\pi}{2}}_0f\left(sinx\right)d\left(sinx\right)\)
Đặt \(sinx=t\Rightarrow t\in\left[0;1\right]\Rightarrow f\left(t\right)=5-t\)
\(I_1=2\int\limits^1_0\left(5-t\right)dt=9\)
Xết \(I_2=3\int\limits^1_0f\left(3-2x\right)dx=-\dfrac{3}{2}\int\limits^1_0f\left(3-2x\right)d\left(3-2x\right)\)
Đặt \(3-2x=t\Rightarrow t\in\left[1;3\right]\Rightarrow f\left(t\right)=t^2+3\)
\(I_2=-\dfrac{3}{2}\int\limits^1_3\left(t^2+3\right)dt=\dfrac{3}{2}\int\limits^3_1\left(t^2+3\right)dt=22\)
\(\Rightarrow I=9+22=31\)
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 11 2021
\(y'=\dfrac{\left(-2x+2\right)\left(x-3\right)-\left(-x^2+2x+c\right)}{\left(x-3\right)^2}=\dfrac{-x^2+6x-6-c}{\left(x-3\right)^2}\)
\(\Rightarrow\) Cực đại và cực tiểu của hàm là nghiệm của: \(-x^2+6x-6-c=0\) (1)
\(\Delta'=9-\left(6+c\right)>0\Rightarrow c< 3\)
Gọi \(x_1;x_2\) là 2 nghiệm của (1) \(\Rightarrow\left\{{}\begin{matrix}-x_1^2+6x_1-6=c\\-x_2^2+6x_2-6=c\end{matrix}\right.\)
\(\Rightarrow m-M=\dfrac{-x_1^2+2x_1+c}{x_1-3}-\dfrac{-x_2^2+2x_2+c}{x_2-3}=4\)
\(\Leftrightarrow\dfrac{-2x_1^2+8x_1-6}{x_1-3}-\dfrac{-2x_2^2+8x_2-6}{x_2-3}=4\)
\(\Leftrightarrow2\left(1-x_1\right)-2\left(1-x_2\right)=4\)
\(\Leftrightarrow x_2-x_1=2\)
Kết hợp với Viet: \(\left\{{}\begin{matrix}x_2-x_1=2\\x_1+x_2=6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=2\\x_2=4\end{matrix}\right.\)
\(\Rightarrow c=2\)
Có 1 giá trị nguyên
27 tháng 11 2023
Câu 2:
a: \(y=\left(2x^2-x+1\right)^{\dfrac{1}{3}}\)
=>\(y'=\dfrac{1}{3}\left(2x^2-x+1\right)^{\dfrac{1}{3}-1}\cdot\left(2x^2-x+1\right)'\)
\(=\dfrac{1}{3}\cdot\left(4x-1\right)\left(2x^2-x+1\right)^{-\dfrac{2}{3}}\)
b: \(y=\left(3x+1\right)^{\Omega}\)
=>\(y'=\Omega\cdot\left(3x+1\right)'\cdot\left(3x+1\right)^{\Omega-1}\)
=>\(y'=3\Omega\left(3x+1\right)^{\Omega-1}\)
c: \(y=\sqrt[3]{\dfrac{1}{x-1}}\)
=>\(y'=\dfrac{\left(\dfrac{1}{x-1}\right)'}{3\cdot\sqrt[3]{\left(\dfrac{1}{x-1}\right)^2}}\)
\(=\dfrac{\dfrac{1'\left(x-1\right)-\left(x-1\right)'\cdot1}{\left(x-1\right)^2}}{\dfrac{3}{\sqrt[3]{\left(x-1\right)^2}}}\)
\(=\dfrac{-x}{\left(x-1\right)^2}\cdot\dfrac{\sqrt[3]{\left(x-1\right)^2}}{3}\)
\(=\dfrac{-x}{\sqrt[3]{\left(x-1\right)^4}\cdot3}\)
d: \(y=log_3\left(\dfrac{x+1}{x-1}\right)\)
\(\Leftrightarrow y'=\dfrac{\left(\dfrac{x+1}{x-1}\right)'}{\dfrac{x+1}{x-1}\cdot ln3}\)
\(\Leftrightarrow y'=\dfrac{\left(x+1\right)'\left(x-1\right)-\left(x+1\right)\left(x-1\right)'}{\left(x-1\right)^2}:\dfrac{ln3\left(x+1\right)}{x-1}\)
\(\Leftrightarrow y'=\dfrac{x-1-x-1}{\left(x-1\right)^2}\cdot\dfrac{x-1}{ln3\cdot\left(x+1\right)}\)
\(\Leftrightarrow y'=\dfrac{-2}{\left(x-1\right)\cdot\left(x+1\right)\cdot ln3}\)
e: \(y=3^{x^2}\)
=>\(y'=\left(x^2\right)'\cdot ln3\cdot3^{x^2}=2x\cdot ln3\cdot3^{x^2}\)
f: \(y=\left(\dfrac{1}{2}\right)^{x^2-1}\)
=>\(y'=\left(x^2-1\right)'\cdot ln\left(\dfrac{1}{2}\right)\cdot\left(\dfrac{1}{2}\right)^{x^2-1}=2x\cdot ln\left(\dfrac{1}{2}\right)\cdot\left(\dfrac{1}{2}\right)^{x^2-1}\)
h: \(y=\left(x+1\right)\cdot e^{cosx}\)
=>\(y'=\left(x+1\right)'\cdot e^{cosx}+\left(x+1\right)\cdot\left(e^{cosx}\right)'\)
=>\(y'=e^{cosx}+\left(x+1\right)\cdot\left(cosx\right)'\cdot e^u\)
\(=e^{cosx}+\left(x+1\right)\cdot\left(-sinx\right)\cdot e^u\)
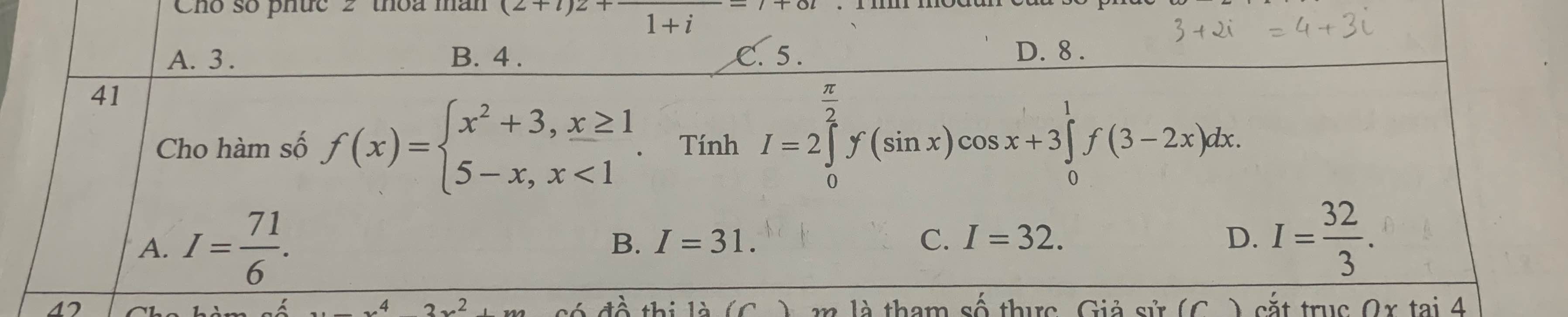
1233211234567899876543210
ko bt nhaaaaaaaaaaaa