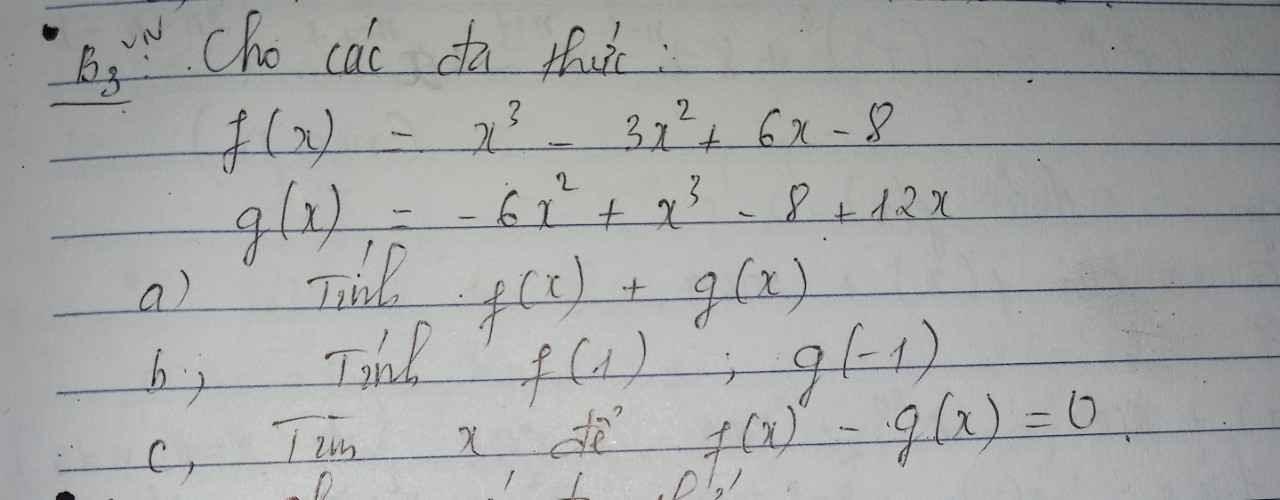Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đặt A = 1+2+2^2+2^3+....+2^60
2A = 2+2^2+2^3+2^4+.....+2^61
2A-A= ( 2+2^2+2^3+....+2^61)-(1+2+2^2+.....+2^60)
A = 2^61-1

\(\frac{1}{12}-\left(-\frac{1}{6}-\frac{1}{4}\right)\)
\(=\frac{1}{12}-\left(-\frac{2}{12}-\frac{3}{12}\right)\)
\(=\frac{1}{12}+\frac{2}{12}+\frac{3}{12}\)
\(=\frac{1}{2}\)
Thanks bạn cute Jeon Koo Koo nhìu nha , tớ cảm ơn pạn rất nhìu :3


a: Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
\(\widehat{KAC}\) chung
Do đó: ΔABH=ΔACK
Suy ra: AH=AK
b: Xét ΔKIB vuông tại K và ΔHIC vuông tại H có
KB=HC
\(\widehat{KBI}=\widehat{HCI}\)
Do đó: ΔKIB=ΔHIC
Suy ra: IK=IH
Xét ΔAKI vuông tại K và ΔAHI vuông tại H có
AI chung
KI=HI
Do đó: ΔAKI=ΔAHI
Suy ra: \(\widehat{KAI}=\widehat{HAI}\)

a: góc ABC=90 độ-góc ACB
góc KHC=90 độ-góc ACB
=>góc ABC=góc KHC
b: Xét ΔBAH vuông tại A và ΔBKH vuông tại K có
BH chung
góc ABH=góc KBH
=>ΔBAH=ΔBKH
=>BA=BK và HA=HK
=>BH là trung trực của AK
c: Xét ΔIBC có
BD,CA là đường cao
BD căt CAt tại H
=>H là trực tâm
=>I,H,K thẳng hàng
d: ΔADK đều
=>góc ADH=30 độ
=>góc AIK=30 độ
=>góc ABC=60 độ

\(f\left(-2\right)=3.\left(-2\right)^2-1=3.4-1=11\\ f\left(\dfrac{1}{2}\right)=3.\left(\dfrac{1}{2}\right)^2-1=3.\left(\dfrac{1}{4}\right)-1=\dfrac{3}{4}-1=-\dfrac{1}{4}\\ f\left(\dfrac{-2}{\sqrt[]{3}}\right)=3.\left(\dfrac{-2}{\sqrt[]{3}}\right)^2-1=3.\left(\dfrac{4}{3}\right)-1=4-1=3\\ f\left(a+1\right)=3.\left(a+1\right)^2-1=3.\left(a^2+2a+1\right)-1=3a^2+6a+3-1=3a^2+6a+2\)



a: \(f\left(x\right)+g\left(x\right)=x^3-3x^2+6x-8+x^3-6x^2+12x-8\)
\(=2x^3-9x^2+18x-16\)
b: \(f\left(1\right)=1^3-3\cdot1^2+6\cdot1-8=1-3+6-8=-2+6-8=4-8=-4\)
\(g\left(-1\right)=-6\cdot\left(-1\right)^2+\left(-1\right)^3-8+12\cdot\left(-1\right)\)
\(=-6\cdot1-1-8-12\)
=-6-21
=-27
c: f(x)-g(x)=0
=>f(x)=g(x)
\(\Leftrightarrow x^3-3x^2+6x-8=x^3-6x^2+12x-8\)
\(\Leftrightarrow3x^2-6x=0\)
=>3x(x-2)=0
=>x=0 hoặc x=2