
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\overrightarrow{u}=4\overrightarrow{MA}-3\left(\overrightarrow{MA}+\overrightarrow{AB}\right)+\overrightarrow{MA}+\overrightarrow{AC}-2\left(\overrightarrow{MA}+\overrightarrow{AD}\right)\)
\(=-3\overrightarrow{AB}+\overrightarrow{AC}-2\overrightarrow{AD}=-3\left(\overrightarrow{AB}+\overrightarrow{AD}\right)+\overrightarrow{AC}+\overrightarrow{AD}\)
\(=-3\overrightarrow{AC}+\overrightarrow{AC}+\overrightarrow{AD}=-2\overrightarrow{AC}+\overrightarrow{AD}\)
\(\overrightarrow{u}^2=\left(-2\overrightarrow{AC}+\overrightarrow{AD}\right)^2=4AC^2-4\overrightarrow{AC}.\overrightarrow{AD}+AD^2\)
\(=4\left(a\sqrt{2}\right)^2-4.a\sqrt{2}.a.cos45^0+a^2=5a^2\)
\(\Rightarrow\left|\overrightarrow{u}\right|=a\sqrt{5}\)


d. \(\dfrac{\pi}{2}< a;b< \pi\Rightarrow sina>0;sinb>0\)
\(sina=\sqrt{1-cos^2a}=\dfrac{4}{5}\Rightarrow tana=\dfrac{sina}{cosa}=-\dfrac{4}{3}\)
\(sinb=\sqrt{1-cos^2b}=\dfrac{5}{13}\Rightarrow tanb=-\dfrac{5}{12}\)
Vậy:
\(sin\left(a-b\right)=sina.cosb-cosa.sinb=\dfrac{4}{5}.\left(-\dfrac{12}{13}\right)-\left(-\dfrac{3}{5}\right)\left(\dfrac{5}{13}\right)=...\)
\(cos\left(a-b\right)=cosa.cosb-sina.sinb=...\) (bạn tự thay số bấm máy)
\(tan\left(a+b\right)=\dfrac{tana+tanb}{1-tana.tanb}=...\)
\(cot\left(a+b\right)=\dfrac{1}{tan\left(a+b\right)}=\dfrac{1-tana.tanb}{tana+tanb}=...\)
e.
\(0< y< \dfrac{\pi}{2}\Rightarrow cosy>0\Rightarrow cosy=\sqrt{1-sin^2y}=\dfrac{4}{5}\)
\(\Rightarrow tany=\dfrac{siny}{cosy}=\dfrac{3}{4}\)
Vậy: \(tan\left(x+y\right)=\dfrac{tanx+tany}{1-tanx.tany}=...\)
\(cot\left(x-y\right)=\dfrac{1}{tan\left(x-y\right)}=\dfrac{1+tanx.tany}{tanx-tany}=...\)


a) \(d\left(A;\Delta\right)=\dfrac{\left|4.1-3.3+2\right|}{\sqrt{4^2+\left(-3\right)^2}}=\dfrac{3}{5}\)
b) \(\overrightarrow{AB}=\left(-3;-2\right)\) là VTCP của đường thẳng d
PT tham số của d: \(\left\{{}\begin{matrix}x=1-3t\\y=3-2t\end{matrix}\right.\left(t\in R\right)\)
c) Đường tròn (C) có bán kính \(R=AB=\sqrt{\left(1+2\right)^2+\left(3-1\right)^2}=\sqrt{13}\)
PT đường tròn (C): \(\left(x-1\right)^2+\left(y-3\right)^2=13\)

9.
Phương trình đường thẳng AB: \(3x-y-7=0\)
Trung điểm đoạn thẳng AB: \(I=\left(2;-1\right)\)
Trung trực đoạn AB vuông góc với AB có phương trình dạng: \(\left(\Delta\right):x+3y+m=0\)
Mà I thuộc \(I\in\Delta\Rightarrow2-3+m=0\Leftrightarrow m=1\)
\(\Rightarrow\Delta:x+3y+1=0\)
10.
Phương trình đường thẳng AB: \(y+4=0\)
Trung điểm đoạn thẳng AB: \(I=\left(2;-4\right)\)
Trung trực đoạn AB vuông góc với AB có phương trình dạng: \(\left(\Delta\right):x+m=0\)
Mà I thuộc \(I\in\Delta\Rightarrow2+m=0=0\Leftrightarrow m=-2\)
\(\Rightarrow\Delta:x-2=0\)




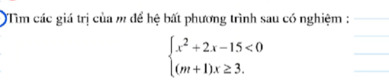
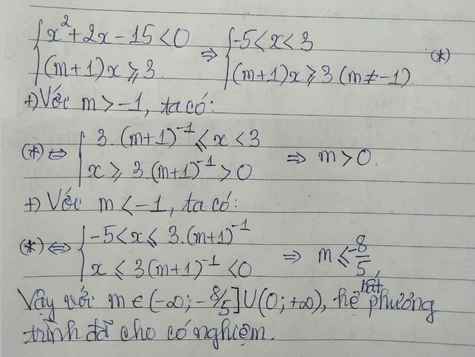






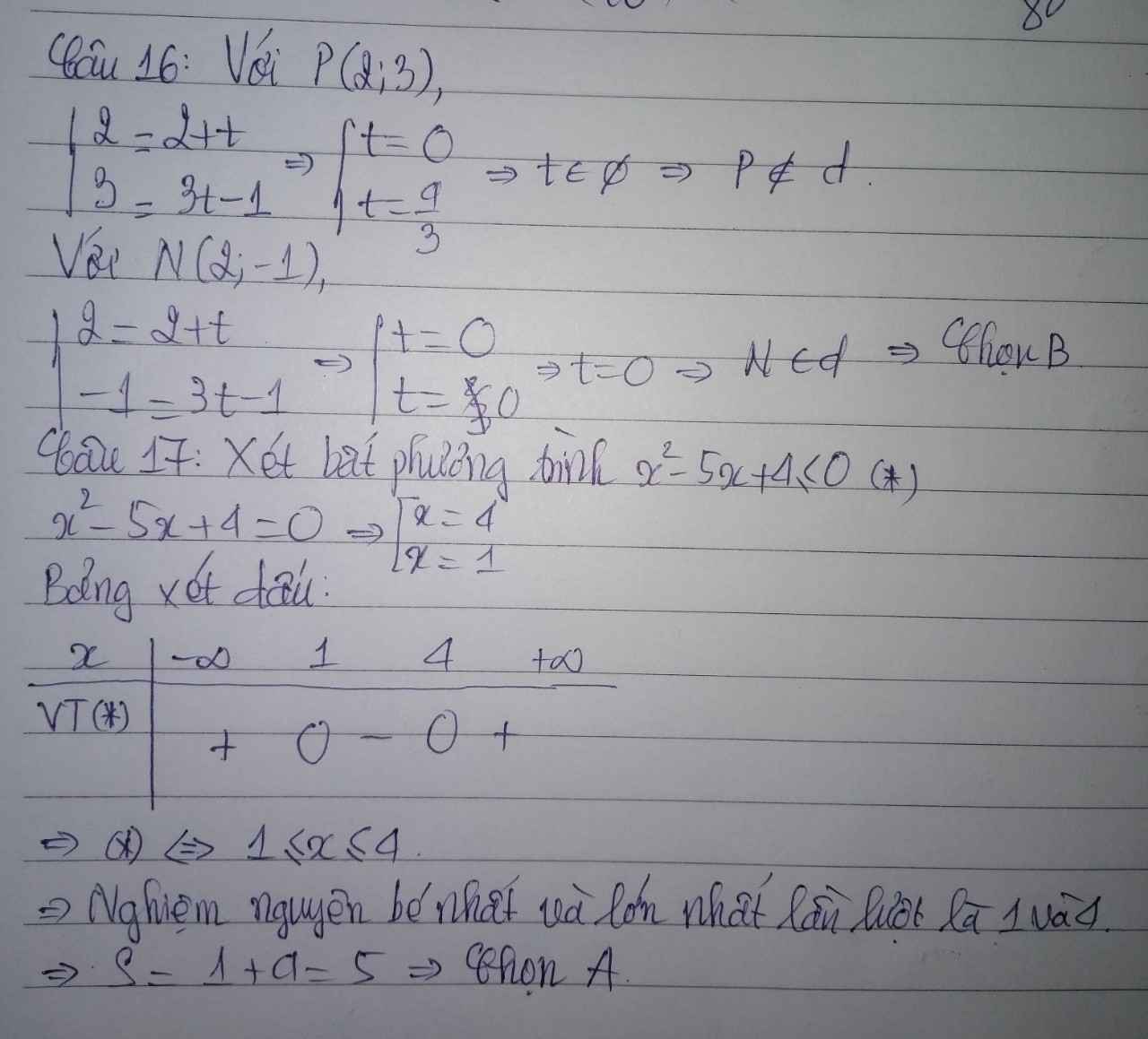
Câu 42:
Δ1: VTPT là (m;-1)
Δ2: VTPT là (2;-1)
Để Δ1 vuông góc Δ2 thì m*2+(-1)*(-1)=0
=>2m+1=0
=>m=-1/2