K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 4 2021
Từ S kẻ \(SH\perp AC\) (1)
Ta có: \(\left\{{}\begin{matrix}SB\perp SA\\SB\perp SC\end{matrix}\right.\) \(\Rightarrow SB\perp\left(SAC\right)\Rightarrow SB\perp AC\) (2)
(1);(2) \(\Rightarrow AC\perp\left(SBH\right)\)
Trong mp (SBH), từ S kẻ \(SK\perp BH\Rightarrow SK\perp\left(ABC\right)\)
\(\Rightarrow SK=d\left(S;\left(ABC\right)\right)\)
\(\dfrac{1}{SH^2}=\dfrac{1}{SA^2}+\dfrac{1}{SC^2}\Rightarrow SH=\dfrac{SA.AC}{\sqrt{SA^2+SC^2}}=\dfrac{a\sqrt{3}}{2}\)
\(\dfrac{1}{SK^2}=\dfrac{1}{SB^2}+\dfrac{1}{SH^2}\Rightarrow SK=\dfrac{SB.SH}{\sqrt{SB^2+SH^2}}=\dfrac{a\sqrt{66}}{11}\)
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 5 2021
\(SA\perp\left(ABC\right)\Rightarrow SA\perp BC\) (1)
Trong mp đáy, kẻ \(AH\perp BC\) (2)
(1);(2) \(\Rightarrow BC\perp\left(SAH\right)\)
Trong mp (SAH), kẻ \(AK\perp SH\Rightarrow AK\perp\left(SBC\right)\)
Hệ thức lượng tam giác vuông ABC: \(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\Rightarrow AH=\dfrac{AB.AC}{\sqrt{AB^2+AC^2}}=\dfrac{a\sqrt{3}}{2}\)
Hệ thức lượng tam giác vuông SAH:
\(\dfrac{1}{AK^2}=\dfrac{1}{AH^2}+\dfrac{1}{SA^2}\Rightarrow AK=\dfrac{AH.SA}{\sqrt{AH^2+SA^2}}=\dfrac{2a\sqrt[]{57}}{19}\)
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 4 2021
Gọi \(M\left(x;y\right)\) là điểm biểu diễn z trên mặt phẳng tọa độ
Gọi \(A\left(-2;1\right)\) ; \(B\left(2;3\right)\) ; \(C\left(-1;2\right)\)
\(\Rightarrow\overrightarrow{AB}=\left(4;2\right)\Rightarrow AB=2\sqrt{5}\)
Từ \(\left|z+2-i\right|+\left|z-2-3i\right|=2\sqrt{5}\Leftrightarrow MA+MB=2\sqrt{5}\)
\(\Leftrightarrow MA+MB=AB\Leftrightarrow\) M nằm trên đoạn thẳng AB
\(\left|z+i-2i\right|=MC\) đạt GTNN khi và chỉ khi M là hình chiếu vuông góc của C lên AB
Phương trình đường thẳng AB:
\(1\left(x+2\right)-2\left(y-1\right)=0\Leftrightarrow x-2y+4=0\)
Phương trình đường thẳng d qua C và vuông góc AB:
\(2\left(x+1\right)+1\left(y-2\right)=0\Leftrightarrow2x+y=0\)
Tọa độ M là nghiệm: \(\left\{{}\begin{matrix}x-2y+4=0\\2x+y=0\end{matrix}\right.\) \(\Rightarrow M\left(-\dfrac{4}{5};\dfrac{8}{5}\right)\)
\(\Rightarrow\overrightarrow{MC}=\left(-\dfrac{1}{5};-\dfrac{2}{5}\right)\Rightarrow MC=\dfrac{\sqrt{5}}{5}\)
Đáp án B
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 4 2021
Xét \(I_1=2\int\limits^{\dfrac{\pi}{2}}_0f\left(sinx\right)cosxdx=2\int\limits^{\dfrac{\pi}{2}}_0f\left(sinx\right)d\left(sinx\right)\)
Đặt \(sinx=t\Rightarrow t\in\left[0;1\right]\Rightarrow f\left(t\right)=5-t\)
\(I_1=2\int\limits^1_0\left(5-t\right)dt=9\)
Xết \(I_2=3\int\limits^1_0f\left(3-2x\right)dx=-\dfrac{3}{2}\int\limits^1_0f\left(3-2x\right)d\left(3-2x\right)\)
Đặt \(3-2x=t\Rightarrow t\in\left[1;3\right]\Rightarrow f\left(t\right)=t^2+3\)
\(I_2=-\dfrac{3}{2}\int\limits^1_3\left(t^2+3\right)dt=\dfrac{3}{2}\int\limits^3_1\left(t^2+3\right)dt=22\)
\(\Rightarrow I=9+22=31\)
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 6 2021
Không ai vẽ hình khi làm bài mặt cầu Oxyz đâu bạn, chỉ cần đại số hóa nó là được.
Gọi I là tâm mặt cầu, do mặt cầu tiếp xúc (Q) tại H nên \(IH\perp\left(Q\right)\)
\(\Rightarrow\) Đường thẳng IH nhận vtpt của (Q) là 1 vtcp
\(\Rightarrow\) IH nhận (1;1;-1) là 1 vtcp
Phương trình IH: \(\left\{{}\begin{matrix}x=1+t\\y=-1+t\\z=-t\end{matrix}\right.\)
I vừa thuộc IH vừa thuộc (P) nên là giao điểm của IH và (P)
\(\Rightarrow\) Tọa độ I thỏa mãn:
\(2\left(1+t\right)+\left(-1+t\right)+\left(-t\right)-3=0\)
\(\Rightarrow t=1\Rightarrow I\left(2;0;-1\right)\)
\(\Rightarrow\overrightarrow{IH}=\left(-1;-1;1\right)\Rightarrow R=IH=\sqrt{3}\)
Phương trình (S):
\(\left(x-2\right)^2+y^2+\left(z+1\right)^2=3\)
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 11 2021
\(y'=\dfrac{\left(-2x+2\right)\left(x-3\right)-\left(-x^2+2x+c\right)}{\left(x-3\right)^2}=\dfrac{-x^2+6x-6-c}{\left(x-3\right)^2}\)
\(\Rightarrow\) Cực đại và cực tiểu của hàm là nghiệm của: \(-x^2+6x-6-c=0\) (1)
\(\Delta'=9-\left(6+c\right)>0\Rightarrow c< 3\)
Gọi \(x_1;x_2\) là 2 nghiệm của (1) \(\Rightarrow\left\{{}\begin{matrix}-x_1^2+6x_1-6=c\\-x_2^2+6x_2-6=c\end{matrix}\right.\)
\(\Rightarrow m-M=\dfrac{-x_1^2+2x_1+c}{x_1-3}-\dfrac{-x_2^2+2x_2+c}{x_2-3}=4\)
\(\Leftrightarrow\dfrac{-2x_1^2+8x_1-6}{x_1-3}-\dfrac{-2x_2^2+8x_2-6}{x_2-3}=4\)
\(\Leftrightarrow2\left(1-x_1\right)-2\left(1-x_2\right)=4\)
\(\Leftrightarrow x_2-x_1=2\)
Kết hợp với Viet: \(\left\{{}\begin{matrix}x_2-x_1=2\\x_1+x_2=6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=2\\x_2=4\end{matrix}\right.\)
\(\Rightarrow c=2\)
Có 1 giá trị nguyên
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 4 2022
\(\left(1+i\right)^{20}=\left(\left(1+i\right)^2\right)^{10}=\left(2i\right)^{10}=\left(\left(2i\right)^2\right)^5=\left(4.i^2\right)^5=\left(-4\right)^5=-2^{10}\)
Cả 4 đáp án đều sai (bạn có thể kiểm tra kết quả dễ dàng bằng chế độ MODE-2 trong casio)
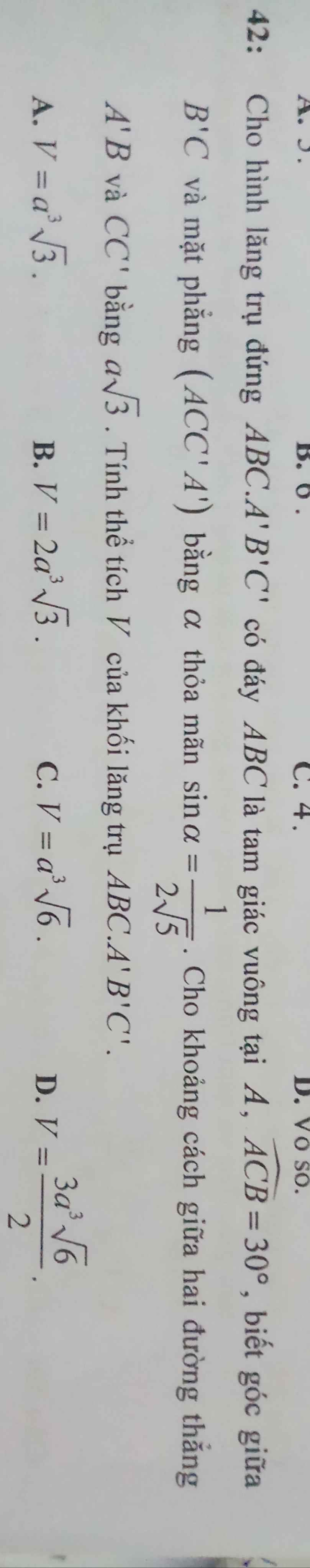
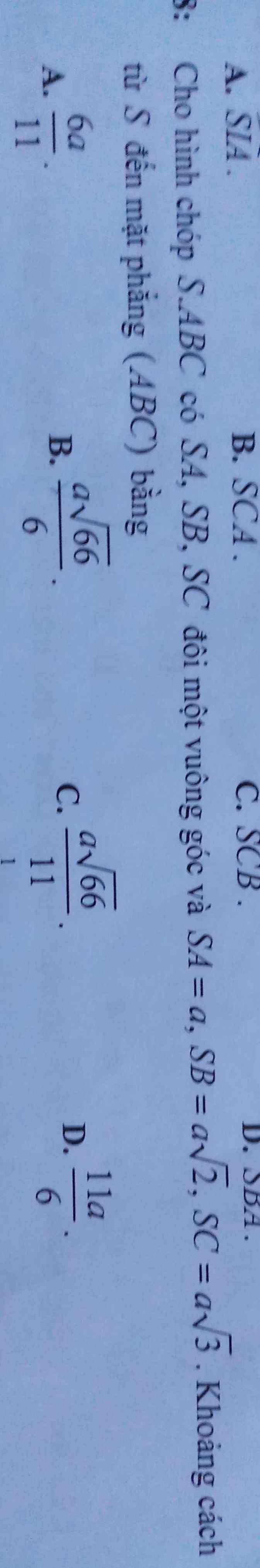
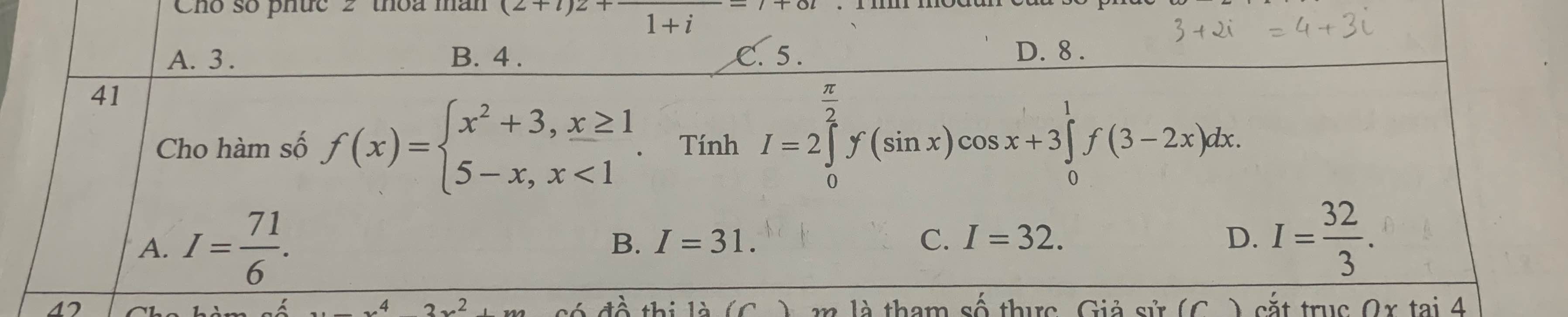
\(\left\{{}\begin{matrix}A'B'\perp AA'\\A'B'\perp A'C'\end{matrix}\right.\) \(\Rightarrow A'B'\perp\left(ACC'A'\right)\)
\(\Rightarrow\widehat{B'CA'}\) là góc giữa \(B'C\) và (ACC'A') \(\Rightarrow sin\widehat{B'CA'}=\dfrac{A'B'}{B'C}=\dfrac{1}{2\sqrt{5}}\)
Mặt khác:
\(CC'||AA'\Rightarrow CC'||\left(ABB'A'\right)\Rightarrow d\left(A'B;CC'\right)=d\left(CC';\left(ABB'A'\right)\right)=d\left(C;\left(ABB'A'\right)\right)=AC\)
\(\Rightarrow AC=a\sqrt{3}\Rightarrow AB=AC.tan30^0=a\)
\(\Rightarrow B'C=2\sqrt{5}A'B'=2a\sqrt{5}\) ; \(BC=\dfrac{AB}{sin30^0}=2a\)
\(\Rightarrow BB'=\sqrt{B'C^2-BC^2}=4a\)
\(V=\dfrac{1}{2}AB.AC.BB'=2a^3\sqrt{3}\)