
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Phương trình đã cho có 2 nghiệm phân biệt khi:
\(\left\{{}\begin{matrix}m-2\ne0\\\Delta'=m^2-m\left(m-2\right)>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\m\ne2\end{matrix}\right.\)
b.
Theo hệ thức Viet ta có: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-2m}{m-2}\\x_1x_2=\dfrac{m}{m-2}\end{matrix}\right.\)
\(Q=\dfrac{1}{x_1}+\dfrac{1}{x_2}+2017=\dfrac{x_1+x_2}{x_1x_2}+2017\)
\(=\dfrac{-2m}{m-2}.\dfrac{m-2}{m}+2017=-2+2017=2015\) là hằng số (đpcm)

Bài 2:
a: \(\text{Δ}=\left[-2\left(m-1\right)\right]^2-4\left(m-4\right)\left(m+3\right)\)
\(=4m^2-4m+1-4\left(m^2-m-12\right)\)
\(=4m^2-4m+1-4m^2+4m+48\)
=49>0
=>Phương trình luôn có hai nghiệm phân biệt
b: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{2\left(m-1\right)}{m-4}\\x_1\cdot x_2=\dfrac{m+3}{m-4}\end{matrix}\right.\)
Theo đề, ta có:
\(\dfrac{4\left(m-1\right)^2}{\left(m-4\right)^2}-2\cdot\dfrac{m+3}{m-4}=9\)
\(\Leftrightarrow4\left(m-1\right)^2-2\left(m+3\right)\left(m-4\right)=9\left(m-4\right)^2\)
\(\Leftrightarrow4m^2-8m+4-2\left(m^2-m-12\right)=9\left(m^2-8m+16\right)\)
\(\Leftrightarrow4m^2-8m+4-2m^2+2m+24-9m^2+72m-144=0\)
\(\Leftrightarrow-7m^2+66m-116=0\)
\(\text{Δ}=66^2-4\cdot\left(-7\right)\cdot\left(-116\right)=1108\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{-66-2\sqrt{277}}{-14}=\dfrac{33+\sqrt{55}}{7}\\x_2=\dfrac{33-\sqrt{55}}{7}\end{matrix}\right.\)
Để phương trình có 2 nghiệm phân biệt \(x_1;x_2.\)
\(\Rightarrow\) \(\Delta'>0.\Leftrightarrow\left(m-1\right)^2-\left(m-4\right)\left(m+3\right)>0.\)
\(\Leftrightarrow m^2-2m+1-m^2-3m+4m+12>0.\)
\(\Leftrightarrow-m+13>0.\Leftrightarrow m< 13.\)
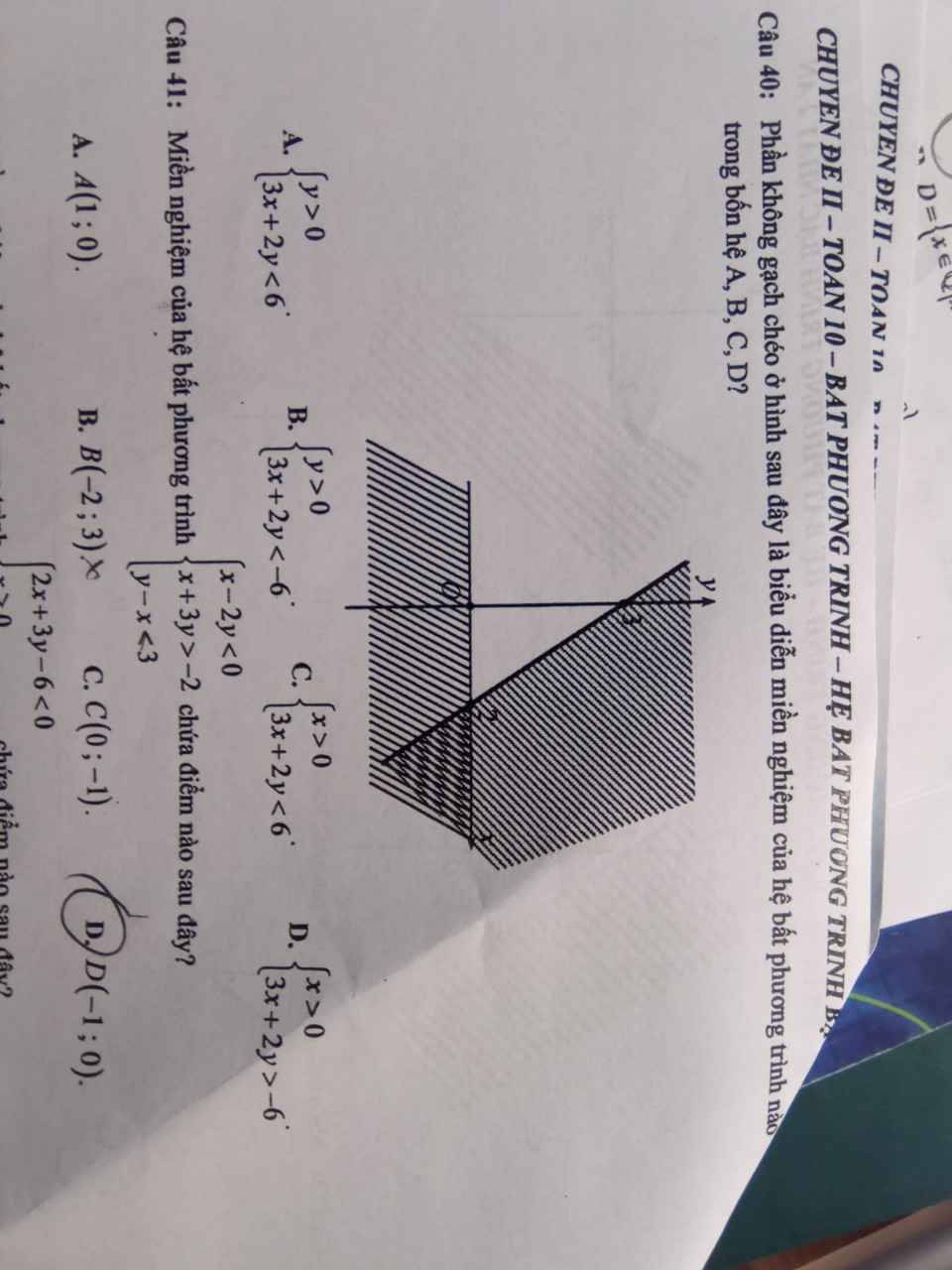



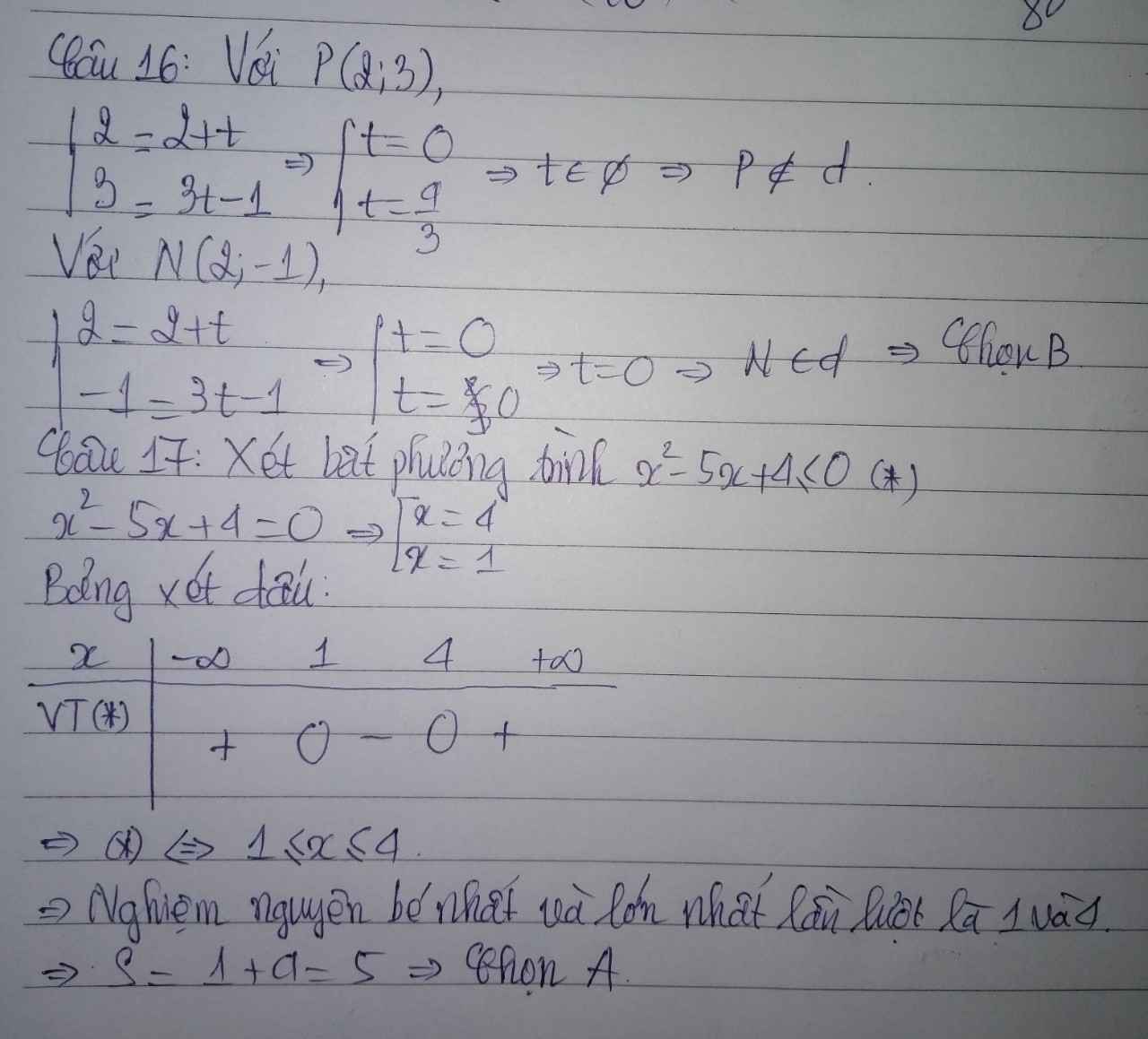
 giúp mình câu 23 trở xuống với mình bí quá
giúp mình câu 23 trở xuống với mình bí quá giúp mình mấy câu này với mình cảm ơn nhìu ạ
giúp mình mấy câu này với mình cảm ơn nhìu ạ
