
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Bảng phân bố tần số (về tuổi thọ bóng đèn điện) có thể viết dưới dạng như sau:

Số trung bình về tuổi thọ của bóng đèn trong bảng phân bố trên là:
.(3x1150 + 6x1160 + 12x1170 + 6x1180 + 3x1190)
= 1170.
b) Số trung bình về chiều dài lá cây dương xỉ trong bài tập 2 trong là:
.(8x15 + 18x25 + 24x35 + 10x45) = 31 (cm).

a) Phương sai và độ lệch chuẩn trong bài tập 1. Bảng phân bố tần số viết lại là
![]()
Số trung bình: \(\overline{x} = 1170\)
Phương sai: \(S_{x}^{2}=\frac{1}{30}(3x1150^{2}+6x1160^{2}+12x1170^{2}+6x1180^{2}+3x1190^{2})-1170^{2} = 120\)
Độ lệch chuẩn: Sx.= \(\sqrt{S_{x}^{2}}=\sqrt{120} ≈ 10,9545\)
b) Phương sai và độ lệch chuẩn, bảng thống kê trong bài tập 2 \(\S 1.\)
\(S_{x}^{2}=\frac{1}{60}(8x15^{2}+18x25^{2}+24x35^{2}+10x45^{2}) - 312 = 84 \)
Sx ≈ 9,165.

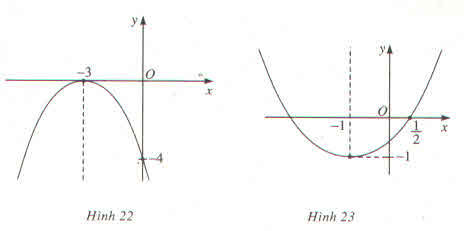
a) Ta thấy đường thẳng \(y=ax+b\) đi qua hai điểm \(\left(0;3\right)\) và \(\left(1;0\right)\). Vậy ta có :
\(\left\{{}\begin{matrix}3=b\\0=a+b\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=-3\\b=3\end{matrix}\right.\)
Đường thẳng có phương trình là \(y=-3x+3\)
b) \(y=-4x\)
c) \(y=x-2\)

a) \(23,3\) phút; \(540^0;27,6^0C\)
b) Khi lấy số trung bình làm đại diện cho các số liệu thống kê về quy mô và độ lớn, có thể xem rằng mỗi ngày bạn A đi từ nhà đến trường đều mất 23,3 phút.
Tương tự, nêu ý nghĩa số trung bình của các số liệu thống kê cho ở bảng 7 và bảng 8.

Hình 22
y=ax^2 +bx+c thỏa mãn hệ
\(\left\{{}\begin{matrix}y\left(0\right)=-4\Rightarrow c=-4\\y\left(-3\right)=9a-3b-4=0\\y\left(-6\right)=36a-6b-4=-4\end{matrix}\right.\)
(3) -(2) nhân 2
\(36a-18a-4+8=-4\Rightarrow18a=-8\Rightarrow a=\dfrac{-8}{18}=\dfrac{-4}{9}\)
Thế vào (2) -4-3b-4=0 => b=-8/3
Vậy pa ra bo; cho hình 22 là
\(y=-\dfrac{4}{9}x^2-\dfrac{8}{3}x-4\)

Bảng cơ cấu giá trị sản suất công gnhiệp trong nước năm 2000 phân theo thành phần kinh tế (%) dựa theo biểu đồ hình quạt đã cho là:















Câu 15 : \(P=tan^3a+cot^3a+tan^2a+cot^2a=\left(tana+cota\right)^3-3tana.cota\left(tana+cota\right)+\left(tana+cota\right)^2-2tana.cota\)
\(=3^3-3.3+3^2-2=25\) . Chọn A
Câu 16 : Đặt a = \(sin^2x;b=cos^2x\Rightarrow a+b=1\)
Ta có : \(3a^2+b^2=\dfrac{3}{4}\) \(\Leftrightarrow3a^2+\left(1-a\right)^2=\dfrac{3}{4}\Leftrightarrow4a^2-2a+\dfrac{1}{4}=0\Leftrightarrow\left(a-\dfrac{1}{4}\right)^2=0\Leftrightarrow a=\dfrac{1}{4}\)
Suy ra : \(a^2=\dfrac{1}{16}\Rightarrow b^2=\dfrac{9}{16}\)
\(P=sin^4x+3cos^4x=a^2+3b^2=\dfrac{1}{16}+3.\dfrac{9}{16}=\dfrac{7}{4}\) . Chọn C