
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Bài 1:
Vận tốc cano khi dòng nước lặng là: $25-2=23$ (km/h)
Bài 2:
Đổi 1 giờ 48 phút = 1,8 giờ
Độ dài quãng đường AB: $1,8\times 25=45$ (km)
Vận tốc ngược dòng là: $25-2,5-2,5=20$ (km/h)
Cano ngược dòng từ B về A hết:
$45:20=2,25$ giờ = 2 giờ 15 phút.

Bài 1:
a.
$a^3-a^2c+a^2b-abc=a^2(a-c)+ab(a-c)$
$=(a-c)(a^2+ab)=(a-c)a(a+b)=a(a-c)(a+b)$
b.
$(x^2+1)^2-4x^2=(x^2+1)^2-(2x)^2=(x^2+1-2x)(x^2+1+2x)$
$=(x-1)^2(x+1)^2$
c.
$x^2-10x-9y^2+25=(x^2-10x+25)-9y^2$
$=(x-5)^2-(3y)^2=(x-5-3y)(x-5+3y)$
d.
$4x^2-36x+56=4(x^2-9x+14)=4(x^2-2x-7x+14)$
$=4[x(x-2)-7(x-2)]=4(x-2)(x-7)$
Bài 2:
a. $(3x+4)^2-(3x-1)(3x+1)=49$
$\Leftrightarrow (3x+4)^2-[(3x)^2-1]=49$
$\Leftrightarrow (3x+4)^2-(3x)^2=48$
$\Leftrightarrow (3x+4-3x)(3x+4+3x)=48$
$\Leftrightarrow 4(6x+4)=48$
$\Leftrightarrow 6x+4=12$
$\Leftrightarrow 6x=8$
$\Leftrightarrow x=\frac{4}{3}$
b. $x^2-4x+4=9(x-2)$
$\Leftrightarrow (x-2)^2=9(x-2)$
$\Leftrightarrow (x-2)(x-2-9)=0$
$\Leftrightarrow (x-2)(x-11)=0$
$\Leftrightarrow x-2=0$ hoặc $x-11=0$
$\Leftrightarrow x=2$ hoặc $x=11$
c.
$x^2-25=3x-15$
$\Leftrightarrow (x-5)(x+5)=3(x-5)$
$\Leftrightarrow (x-5)(x+5-3)=0$
$\Leftrightarrow (x-5)(x+2)=0$
$\Leftrightarrow x-5=0$ hoặc $x+2=0$
$\Leftrightarrow x=5$ hoặc $x=-2$

\(1.\left(x+4\right)^2-\left(x-1\right)\left(x+1\right)=16\Leftrightarrow x^2+8x+16-x^2+1=16\)
\(\Leftrightarrow8x=-1\Leftrightarrow x=-\frac{1}{8}\)
\(2.\left(x-1\right)^2+\left(x+3\right)^2+2\left(x-1\right)\left(x+3\right)=4\Leftrightarrow\left(x-1+x+3\right)^2=4\)
\(\Leftrightarrow\left(2x+2\right)^2=4\Leftrightarrow\orbr{\begin{cases}2x+2=2\\2x+2=-2\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=0\\x=-2\end{cases}}\)
3.\(\left(x-1\right)^2-x\left(x-1\right)=0\Leftrightarrow\left(x-1\right)\left[\left(x-1\right)-x\right]=0\Leftrightarrow x-1=0\Leftrightarrow x=1\)
\(4.\left(3x-1\right)^2+\left(5x-2\right)^2-2\left(3x-1\right)\left(5x-2\right)=9\Leftrightarrow\left(3x-1-5x+2\right)^2=9\)
\(\Leftrightarrow\left(2x-1\right)^2=9\Leftrightarrow\orbr{\begin{cases}2x-1=3\\2x-1=-3\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=2\\x=-1\end{cases}}\)
5.\(\left(x-1\right)\left(x^2+x+1\right)-x\left(x-2\right)\left(x+2\right)=5\Leftrightarrow x^3-1-\left(x^3-4x\right)=5\)
\(\Leftrightarrow4x=6\Leftrightarrow x=\frac{3}{2}\)
6.\(\left(x-1\right)^3-\left(x+3\right)\left(x^2-3x+9\right)+\left(x-2\right)\left(x+2\right)=2\)
\(\Leftrightarrow x^3-3x^2+3x-1-\left(x^3+27\right)+x^2-4=2\)
\(\Leftrightarrow-2x^2+3x-34=0\text{ vô nghiệm}\)

b) Bạn đã chứng minh được tứ giác EKFC là hình bình hành ở câu a, mà EF cắt CK tại I \(\Rightarrow\)I là trung điểm EF (tính chất hình bình hành)
\(\Rightarrow AI\)là trung tuyến của \(\Delta AEF\)
Mà \(\Delta AEF\)vuông tại A \(\Rightarrow AI=\frac{1}{2}EF\)(tính chất tam giác vuông)
Lại có \(EI=\frac{1}{2}EF\)do I là trung điểm của đoạn EF \(\Rightarrow AI=EI\left(=\frac{1}{2}EF\right)\)
Mặt khác \(BE\perp AF\), \(MI\perp AF\left(gt\right)\)\(\Rightarrow BE//MI\)(quan hệ từ vuông góc đến song song)
Mà tứ giác BEFD là hình bình hành \(\Rightarrow BD//EF\)(tính chất hình bình hành)
\(\Rightarrow BM//EI\)(vì \(M\in BD;I\in EF\))
Xét tứ giác BEIM có \(BE//MI\left(cmt\right);BM//EI\left(cmt\right)\)\(\Rightarrow\)Tứ giác BEIM là hình bình hành (định nghĩa)
\(\Rightarrow BM=EI\)(tính chất hình bình hành)
Mà \(AI=EI\left(cmt\right)\)\(\Rightarrow AI=BM\left(=EI\right)\left(đpcm\right)\)
c) Do tứ giác BEFD là hình bình hành \(\Rightarrow\hept{\begin{cases}BE//DF\\BE=DF\end{cases}}\)(tính chất hình bình hành)
Mà \(\hept{\begin{cases}BE\perp CF\\BE=CF\end{cases}}\left(gt\right)\Rightarrow\hept{\begin{cases}DF\perp CFtạiF\\DF=CF\end{cases}}\)\(\Rightarrow\)F nằm trên đường trung trực của đoạn CD và \(\Delta CDF\)vuông cân tại F
\(\Rightarrow\widehat{DCF}=45^0\)
\(\Delta ABC\)vuông cân tại A (gt) \(\Rightarrow\widehat{ACB}=45^0\)
\(\Rightarrow\widehat{BCD}=180^0-\widehat{ACB}-\widehat{DCF}=180^0-45^0-45^0=90^0\)
\(\Rightarrow\Delta BCD\)vuông tại C.
Xét hình thang BEFD (BE//DF) ta có I là trung điểm EF (cmt) và IM//BE (cmt) \(\Rightarrow\)M là trung điểm của đoạn BD
\(\Rightarrow\)CM là trung tuyến của \(\Delta BCD\)
Mặt khác \(\Delta BCD\)vuông tại C \(\Rightarrow CM=\frac{1}{2}BD\)(tính chát tam giác vuông)
Mà \(DM=\frac{1}{2}BD\)do M là trung điểm BD \(\Rightarrow DM=CM\left(=\frac{1}{2}BD\right)\)
\(\Rightarrow\)M nằm trên đường trung trực của đoạn CD.
Mà F cũng nằm trên đường trung trực của đoạn CD (cmt)
\(\Rightarrow\)MF là đường trung trực của đoạn CD \(\Rightarrow\)C đối xứng với D qua MF (đpcm)

A. Trắc nghiệm: 1.A; 2.B; 3.D; 4.D; 5.B; 6.C; 7.B; 8.C
B. Tự luận
Bài 4:
a/ Ta có AB//CD; \(AM\in AB;CN\in CD\) => AM//CN
AN//CM (gt)
=> AMCN là hbh (Tứ giác có các cặp cạnh đối // với nhau từng đôi 1 là hbh)
b/ Ta có
AD//CD; \(CI\in BC\) => AD//CI
AD=BC mà BC=CI => AD=CI
=> ACID là hbh (Tứ giác có cặp cạnh đối // và bằng nhau là hbh) => AC=DI (trong hbh các cặp cạnh đối = nhau từng đôi 1)
c/
Ta có
AM=BM (gt) \(\Rightarrow AM=\frac{AB}{2}\) mà AB=CD \(\Rightarrow AM=\frac{CD}{2}\)
Mà AMCN là hbh => AM=CN => \(CN=\frac{CD}{2}\) => N là trung điểm của CD (1)
AMCN là hbh => OA=OC (trong hbh 2 đường chéo cắt nhau tại trung điểm mỗi đường) => O là trung điểm của AC (2)
Từ (1) và (2) => NO là đường trung binhd của tg ACD (đường thẳng đi qua trung điểm của 2 cạnh một tam giác là đường trung bình)
d/ Trong hbh ACID nối AI cắt CD tại N' => N' là trung điểm của CD (trong hbh 2 đường chéo cắt nhau tại trung điểm mỗi đường)
Mà N là trung điểm của CD (cmt)
=> N trùng N'
Ta có
AMCN là hbh => MC//AN (Trong hbh các cặp cạnh đối // với nhau từng đôi 1)
Mà \(NI\in AN\)
=> MC//NI
Bài 5
\(A=-\left(y^4-8y^2+16\right)+20=-\left(y^2-4\right)^2+20\)
Ta có \(\left(y^2-4\right)\ge0\Rightarrow-\left(y^2-4\right)^2\le0\)
\(\Rightarrow A=-\left(y^2-4\right)+20\le20\)
Vậy giá trị lớn nhất của A là 20
Bài 5 (tiếp)
\(-\left(y^2-4\right)+20=20\Rightarrow y^2-4=0\Rightarrow y^2=4\Rightarrow y=\pm2\)
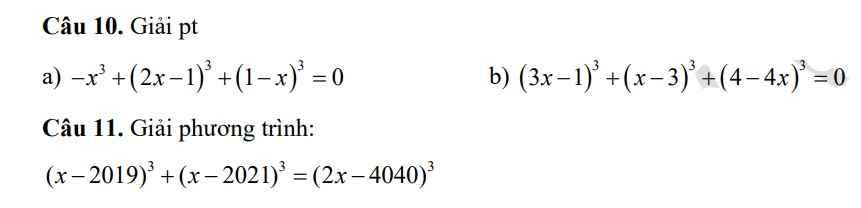




 Mọi Người giải giúp em ạ em cảm ơn ạ
Mọi Người giải giúp em ạ em cảm ơn ạ 

 mọi người giải giúp em với ạ em đang cần gấp lắm ạ
mọi người giải giúp em với ạ em đang cần gấp lắm ạ 






 Mình cần giải bài 6 ạ, giúp mình với huhu ;-;
Mình cần giải bài 6 ạ, giúp mình với huhu ;-; GIÚP MÌNH BÀI 4 CÂU B,C THÔI Ạ MÌNH CẢM ƠN NHIỀU
GIÚP MÌNH BÀI 4 CÂU B,C THÔI Ạ MÌNH CẢM ƠN NHIỀU
Câu 10:
a: \(\Leftrightarrow-x^3+8x^3-12x^2+6x-1+1-3x+3x^2-x^3=0\)
\(\Leftrightarrow6x^3-9x^2+3x=0\)
\(\Leftrightarrow3x\left(2x^2-3x+1\right)=0\)
\(\Leftrightarrow x\left(2x-1\right)\left(x-1\right)=0\)
hay \(x\in\left\{0;\dfrac{1}{2};1\right\}\)
b: Đặt 3x-1=a; x-3=b
Theo đề, ta có: \(a^3+b^3-\left(a+b\right)^3=0\)
\(\Leftrightarrow a^3+b^3-a^3-b^3-3a^2b-3ab^2=0\)
\(\Leftrightarrow3ab\left(a+b\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-1=0\\x-3=0\\4-4x=0\end{matrix}\right.\Leftrightarrow x\in\left\{\dfrac{1}{3};3;1\right\}\)