
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1 :
Khẳng định b) sai vì |-2,5| > 0
Các khẳng định a) và c) đúng
Bài 2 :
Nếu |x| = y thì x = y hoặc x = -y. theo công thức trên thì :
a) x = \(\frac{1}{5}\) hoặc x = \(-\frac{1}{5}\)
b) x = 0,37 hoặc x = -0,37
c) x = 0
d) x = \(1\frac{2}{3}\) hoặc x = \(-1\frac{2}{3}\)


Ta có: \(\left(x-3.5\right)^2\ge0\forall x\)
\(\left(y-\dfrac{1}{10}\right)^4\ge0\forall y\)
Do đó: \(\left(x-3.5\right)^2+\left(y-\dfrac{1}{10}\right)^4\ge0\forall x,y\)
Dấu '=' xảy ra khi \(\left(x,y\right)=\left(\dfrac{7}{2};\dfrac{1}{10}\right)\)
do
\(\left(x-3.5\right)^2+\left(y-\dfrac{1}{10}\right)^4\ge0\)
mà ta có \(\left(x-3.5\right)^2+\left(y-\dfrac{1}{10}\right)^4\le0\)
nên \(\left(x-3.5\right)^2+\left(y-\dfrac{1}{10}\right)^4=0\)
suy ra \(\left\{{}\begin{matrix}x-3,5=0\\y-\dfrac{1}{10}=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=3,5\\y=\dfrac{1}{10}\end{matrix}\right.\)
tick mik nha

\(A=\dfrac{2^{13}\cdot3^7}{2^{15}\cdot3^2\cdot9^2}=\dfrac{2^{13}\cdot3^7}{2^{15}\cdot3^6}=\dfrac{3}{4}\)
\(C=27\cdot\left(-\dfrac{3}{2}\right)^{-5}\cdot\left(-\dfrac{2}{5}\right)^{-4}:\left(\dfrac{2}{125}\right)^{-1}\)
\(=27\cdot\dfrac{-32}{243}\cdot\dfrac{625}{16}\cdot\dfrac{2}{125}\)
\(=\dfrac{-32}{9}\cdot\dfrac{1}{8}\cdot5\)
\(=-\dfrac{20}{9}\)

c: Ta có: \(\left(\dfrac{1}{2}\right)^{2x+1}=\dfrac{1}{8}\)
\(\Leftrightarrow2x+1=3\)
\(\Leftrightarrow2x=2\)
hay x=1
d: Ta có: \(\left(-\dfrac{1}{3}\right)^{x+3}=\dfrac{1}{81}\)
\(\Leftrightarrow x+3=4\)
hay x=1

ta có 33/131 < 33/217< 53/217
=> 33/131< 53/217
# Linh 2k7#
trả lời
33/131>33/132=1/4
53/217<53/212=1/4 hay 53/217<1/4<33/131
Vậy 53/217<33/131
hc tốt ~:B~



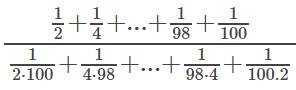

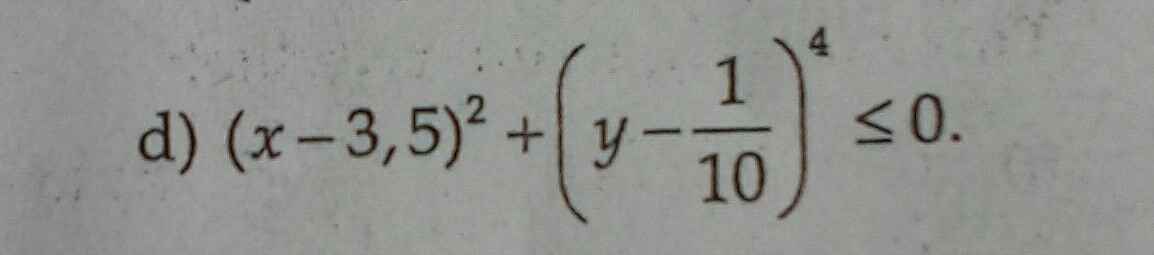
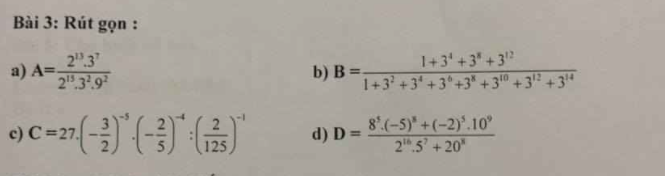 giúp mình với ạ cả 4 câu càng nhanh càng tốt
giúp mình với ạ cả 4 câu càng nhanh càng tốt giúp mình với ạ càng nhanh càng tốt 4 câu trên ạ
giúp mình với ạ càng nhanh càng tốt 4 câu trên ạ
 giải giúp mình với càng nhanh càng tốt
giải giúp mình với càng nhanh càng tốt
Tử số:
\(\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{98}+\dfrac{1}{100}\)
\(=(\dfrac{1}{2}+\dfrac{1}{100})+(\dfrac{1}{4}+\dfrac{1}{98})+...+\left(\dfrac{1}{48}+\dfrac{1}{54}\right)+(\dfrac{1}{50}+\dfrac{1}{52})\)
\(=\dfrac{102}{2.100}+\dfrac{102}{4.98}+...+\dfrac{102}{48.54}+\dfrac{102}{50.52}\)
\(=102\left(\dfrac{1}{2.100}+\dfrac{1}{4.98}+...+\dfrac{1}{48.54}+\dfrac{1}{50.52}\right)\)
Mẫu số:
\(\dfrac{1}{2.100}+\dfrac{1}{4.98}+...+\dfrac{1}{98.4}+\dfrac{1}{100.2}\)
\(=\dfrac{2}{2.100}+\dfrac{2}{4.98}+....+\dfrac{2}{48.54}+\dfrac{2}{50.52}\)
\(=2\left(\dfrac{1}{2.100}+\dfrac{1}{4.98}+...+\dfrac{1}{48.54}+\dfrac{1}{50.52}\right)\)
Chia cả tử và mẫu cho \(=\dfrac{1}{2.100}+\dfrac{1}{4.98}+...+\dfrac{1}{48.54}+\dfrac{1}{50.52}\)
ta được \(\dfrac{tử}{mẫu}=\dfrac{102}{2}=51\)
Đs:....