
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Bài 1
Mình làm mẫu một số câu thôi nhé
\(9,\sqrt{5}=\left(\sqrt{5}\right)^2=5\\ \sqrt{6}=\left(\sqrt{6}\right)^2=6\)
Vì \(5< 6\)
\(\Rightarrow\sqrt{5}< \sqrt{6}\)
\(10,2\sqrt{5}=\left(2\sqrt{5}\right)^2=20\\ \sqrt{7}=\left(\sqrt{7}\right)^2=7\)
Vì \(20>7\)
\(\Rightarrow2\sqrt{5}>\sqrt{7}\)
\(11,5\sqrt{2}=\left(5\sqrt{2}\right)^2=50\\ 2\sqrt{3}=\left(2\sqrt{3}\right)^2=12\)
Vì \(50>12\Rightarrow5\sqrt{2}>2\sqrt{3}\)
\(12,2\sqrt{6}=\left(2\sqrt{6}\right)^2=24\\ 5=5^2=25\)
Vì \(25>24\Rightarrow5>2\sqrt{6}\)
\(13,\sqrt{7}=\left(\sqrt{7}\right)^2=7\\ 2=2^2=4\)
Vì \(7>4\Rightarrow\sqrt{7}>2\)
\(14,3=3^2=9\\ \sqrt{5}=\left(\sqrt{5}\right)^2=5\)
Vì \(9>5\Rightarrow3>\sqrt{5}\)
\(15,3\sqrt{6}=\left(3\sqrt{6}\right)^2=54\)
Vì \(54>1\Rightarrow3\sqrt{6}>1\)
\(16,2\sqrt{2}=\left(2\sqrt{2}\right)^2=8\\ 3=3^2=9\)
Vì \(8< 9\Rightarrow2\sqrt{2}< 3\)
Phương pháp làm dạng bài này là bình phương hai vế rồi so sánh
Bài 2
Gợi ý : Biểu thức dưới dấu căn \(\ge\) 0
Lưu ý : Nếu biểu thức dưới dấu căn ở dưới mẫu thì \(>0\)
\(21,ĐK:4x^2-12x+9>0\\ \Rightarrow\left(2x-3\right)^2>0\\ \Leftrightarrow x\ne\dfrac{3}{2}\)
\(22,ĐK:x^2-8x+15\ge0\\ \Rightarrow\left[{}\begin{matrix}x\le3\\x\ge5\end{matrix}\right.\)
\(23,ĐK:\left\{{}\begin{matrix}x-2\ge0\\x-5\ne0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x\ge2\\x\ne5\end{matrix}\right.\)
\(24,ĐK:\left\{{}\begin{matrix}\dfrac{2+x}{5-x}\ge0\\5-x\ne0\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}2+x\ge0\\5-x\ge0\\x\ne5\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x\ge-2\\x\le5\\x\ne5\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x\ge-2\\x< 5\end{matrix}\right.\left(t/m\right)\)
Hoặc
\(\left\{{}\begin{matrix}2+x\le0\\5-x\le0\\5-x\ne0\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x\le-2\\x\ge5\\x\ne5\end{matrix}\right.\left(loại\right)\)

a: Gọi (d):y=ax+b là phương trình đường thẳng đi qua hai điểm M và N
(d) đi qua M(3;-1) nên thay x=3 và y=-1 vào (d), ta được:
3a+b=-1
(d) đi qua N(-2;-2) nên thay x=-2 và y=-2 vào (d), ta được:
-2a+b=-2
Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}3a+b=-1\\-2a+b=-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}5a=1\\3a+b=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{1}{5}\\b=-1-3a=-1-\dfrac{3}{5}=-\dfrac{8}{5}\end{matrix}\right.\)
=>(d): \(y=\dfrac{1}{5}x-\dfrac{8}{5}\)
c: Gọi (d): y=ax+b là phương trình đường thẳng đi qua hai điểm P,Q
(d) đi qua P(2;3) nên thay x=2 và y=3 vào (d), ta được:
2a+b=3
(d) đi qua Q(-2;-1) nên thay x=-2 và y=-1 vào (d), ta được:
-2a+b=-1
Do đó, ta có hệ phương trình:
\(\left\{{}\begin{matrix}2a+b=3\\-2a+b=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2b=2\\2a+b=3\end{matrix}\right.\)
=>b=1 và 2a=3-b=2
=>b=1 và a=1
=>(d): y=x+1

\(x^2+\sqrt{5}x-10=0\)
\(\Delta=5-4\left(-10\right)=45>0\)
Vậy pt có nghiệm pb
\(x_1=\dfrac{-\sqrt{5}-3\sqrt{5}}{2}=-2\sqrt{5};x_2=\dfrac{-\sqrt{5}+3\sqrt{5}}{2}=\sqrt{5}\)

2:
a: =>x^2(5x^2+2)+2=0
x^2>=0
5x^2+2>=2
=>x^2(5x^2+2)>=0 với mọi x
=>x^2(5x^2+2)+2>=2>0 với mọi x
=>PTVN
b: x^4-12x^2+24=0
=>x^4-12x^2+36-12=0
=>(x^2-6)^2-12=0
=>(x^2-6-2căn 3)(x^2-6+2căn 3)=0
=>x^2=6+2căn 3 hoặc x^2=6-2căn 3
=>\(x=\pm\sqrt{6+2\sqrt{3}};x=\pm\sqrt{6-2\sqrt{3}}\)

1:

4:
a: \(B=\dfrac{x-x+\sqrt{x}}{\sqrt{x}-1}=\dfrac{\sqrt{x}}{\sqrt{x}-1}\)
Khi x=9/25 thì B=3/5:(3/5-1)=3/5:(-2/5)=-3/2
b: \(A=\dfrac{x-1+\sqrt{x}+2-x}{x-\sqrt{x}}=\dfrac{\sqrt{x}+1}{x-\sqrt{x}}\)
c: P=B:A
\(=\dfrac{\sqrt{x}}{\sqrt{x}-1}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\sqrt{x}+1}=\dfrac{x}{\sqrt{x}+1}\)
P nguyên
=>x-1+1 chia hết cho căn x+1
=>căn x+1 thuộc Ư(1)
=>căn x+1=1 hoặc căn x+1=-1
=>căn x=-2(loại) hoặc căn x=0(loại)

\(b,\) Với giá trị đã tim được ở câu a, ta tiếp tục làm câu b
\(A-\dfrac{2}{\sqrt{3}}=\dfrac{\sqrt{x}}{\sqrt{x}-2}-\dfrac{2}{\sqrt{3}}\)\(\left(1\right)\)
Thay \(x=7+4\sqrt{3}\) vào \(\left(1\right)\)
\(\Rightarrow\dfrac{\sqrt{7+4\sqrt{3}}}{\sqrt{7+4\sqrt{3}}-2}-\dfrac{2}{\sqrt{3}}\)
\(=1\)
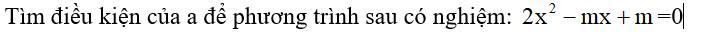


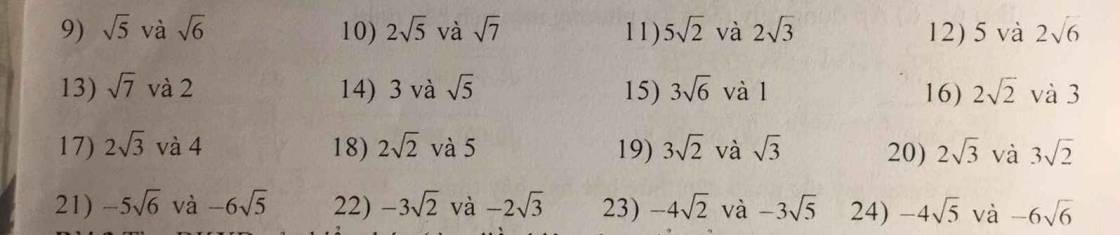
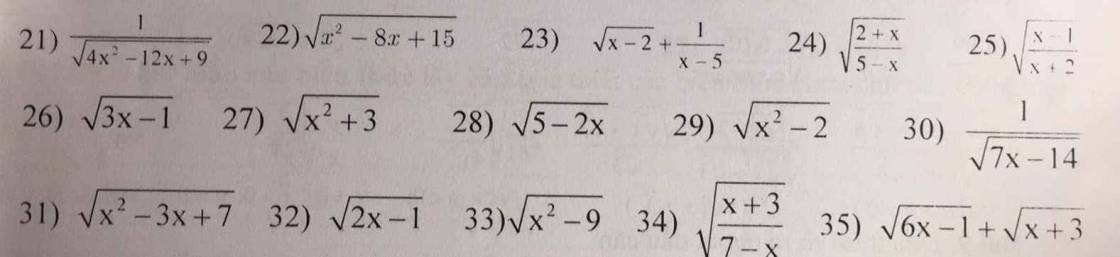
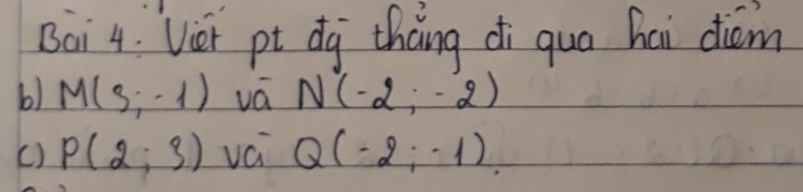
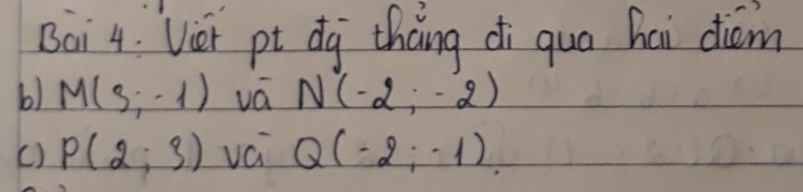



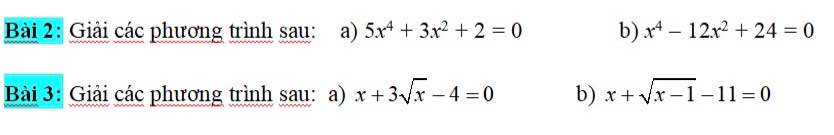
 Giúp mk mấy bài này vs ạ
Giúp mk mấy bài này vs ạ
Ta có:
\(\Delta=b^2-4ac=\left(-m\right)^2-4.2.m\) \(=m^2-8m\)
Để phương trình có nghiệm thì \(\Delta\ge0\)
\(\Rightarrow m^2-8m\ge0\Leftrightarrow\left[{}\begin{matrix}m\le0\\m\ge8\end{matrix}\right.\)