K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
Thông cảm mk bị cận!
28 tháng 7 2017
Bài 1:
x y m B A C 1 1 2 1
Qua B, vẽ tia Bm sao cho Bm // Ax
Bm // Ax ( cách vẽ ) => góc A1 + góc B1 = 180o ( trong cùng phía )
Mà góc A1 = 140o ( giả thiết ) => góc B1 = 40o
Ta có: góc B1 + góc B2 = góc ABC
Mà góc ABC = 70o ( giả thiết ); góc B1 = 40o ( chứng minh trên )
=> góc B2 = 30o
Ta có: góc B2 + góc C1 = 30o + 150o = 180o
Mà hai góc này ở vị trí trong cùng phía
=> Bm // Cy ( dấu hiệu nhận biết 2 đường thẳng song song )
Ta lại có:
Ax // Bm ( cách vẽ ); Cy // Bm ( chứng minh trên )
=> Ax // Cy ( tính chất 3 quan hệ từ vuông góc đến song song ) ( đpcm )
Bài 3:
A B C F E G N M H 1 2
a) Chứng minh AH < \(\dfrac{1}{2}\) ( AB + AC )
+) Vì AH vuông góc với BC ( giả thiết )
=> AH < AB ( quan hệ giữa đường vuông góc và đường xiên ) ( 1 )
+) Vì AH vuông góc với BC ( giả thiết )
=> AH < AC ( quan hệ giữa đường vuông góc và đường xiên ) ( 2 )
+) Từ ( 1 ) và ( 2 ) => AH + AH < AB + AC
=> 2 . AH < AB + AC
=> AH < \(\dfrac{1}{2}\) ( AB + AC ) ( đpcm )
b) Chứng minh EF = BC
+) Vì BM là đường trung tuyến của tam giác ABC ( giả thiết )
=> \(\dfrac{BG}{BM}=\dfrac{2}{3}\)
=> \(\dfrac{MG}{BG}=\dfrac{1}{2}\)
=> 2 . MG = BG
Mà EM = MG ( do BM là đường trung tuyến của tam giác ABC )
=> EM + MG = BG => EG = BG
+) Vì CN là đường trung tuyến của tam giác ABC ( giả thiết )
=> \(\dfrac{CG}{CN}=\dfrac{2}{3}\)
=> \(\dfrac{GN}{CG}=\dfrac{1}{2}\)
=> 2 . GN = CG
Mà FN = GN ( do CN là đường trung tuyến của tam giác ABC )
=> FN + GN = CG => FG = CG
Góc G1 = góc G2 ( đối đỉnh )
Xét tam giác FEG và tam giác CBG có:
FG = CG ( chứng minh trên )
EG = BG ( chứng minh trên )
Góc G1 = góc G2 ( chứng minh trên )
=> tam giác FEG = tam giác CBG ( c.g.c )
=> EF = BC ( 2 cạnh tương ứng ) ( đpcm )
DN
12 tháng 5 2017
| Giá trị (x) | Tần số (n) | Các tích (x.n) | |
| 17 | 3 | 51 | |
| 18 | 5 | 90 | |
| 19 | 4 | 76 | |
| 20 | 2 | 40 | |
| 21 | 3 | 63 | |
| 22 | 2 | 44 | |
| 24 | 3 | 72 | |
| 26 | 3 | 78 | |
| 28 | 1 | 28 | |
| 30 | 1 | 30 | |
| 31 | 2 | 62 | |
| 32 | 1 | 32 | |
| N = 30 | Tổng: 666 |
25 tháng 10 2017
| Phép tính | Ước lương kết quả | ĐS đúng |
| 24.68:12 | 20.70:10 = 140 | 136 |
| 7,8.3,1:1,6 | 8.3:2=12 | 15,1125 |
| 6,9.72:24 | 7.70:20 = 24,5 | 20,7 |
| 56.9,9:8,8 | 60.10:9 = 66,(6) | 63 |
| 0,38.0,45:0,95 | 0.0:1=0 | 0,18 |
SG
1
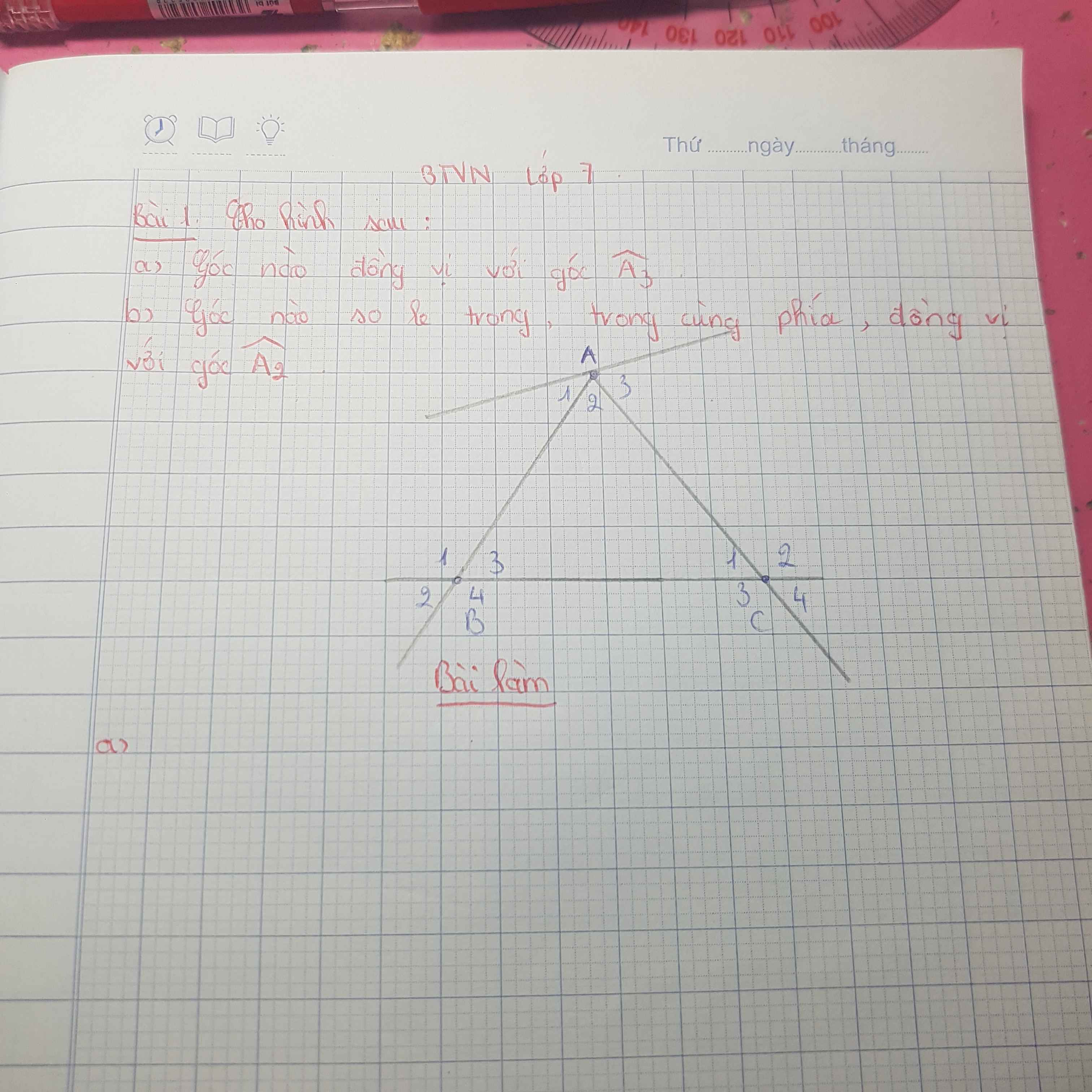
a) Góc đồng vị với góc A3 là góc C4
b) Góc so le trong với góc A2 là góc B1 và góc C2
Góc trong cùng phía với góc A2 là góc B3 và góc C1
Góc đồng vị với góc A2 là góc B4 và góc C3